Anatomie d’un condensateur

Nouvelle Calédonie 2022 Sujet 2

Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ2NC1

Mots clefs de l’EXERCICE C : condensateur, capacité, circuit RC série

Les polycarbonates sont de bons isolants et, à ce titre, sont employés en électronique pour la fabrication de condensateurs. Les condensateurs au polycarbonate sont réalisés en alternant des feuilles métallisées avec des feuilles de polycarbonate un grand nombre de fois. Ces types de condensateurs ont des capacités qui ne varient pas beaucoup avec la température. Ils peuvent avoir des tensions de fonctionnement allant jusqu’à 400 V crête à crête et peuvent être utilisés dans un intervalle de température allant de -55 °C à +125 °C.

Dans la partie A la capacité d’un condensateur au polycarbonate est déterminée dans le cadre du modèle du circuit RC puis, dans la partie B, l’étude porte sur l’anatomie de ce condensateur.

Partie A : Détermination de la capacité d’un condensateur au polycarbonate

On considère le circuit électrique dont le schéma est représenté ci-dessous dans lequel le générateur de tension est idéal et délivre une tension électrique E = 12 V :

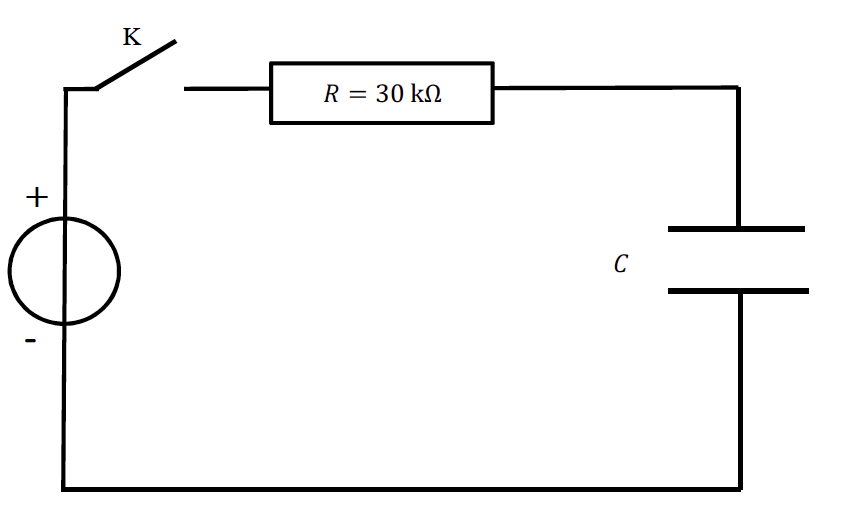
Le condensateur, de capacité C, est initialement déchargé. À l’instant t = 0, on ferme l’interrupteur K.

A.1. Recopier le schéma du circuit sur la copie, puis indiquer le sens du courant électrique, d’intensité i, circulant dans le circuit durant le régime transitoire, ainsi que les tensions E, u_R et u_C prises respectivement aux bornes du générateur, du conducteur ohmique de résistance R et du condensateur de capacité C.

A.2. Établir la relation entre les tensions électriques dans ce circuit.

Réponse :

D’après la loi d’additivité des tensions ou loi des mailles :

$E=U_C(t)+U_R(t)$

A.3. Exprimer la charge q du condensateur en fonction de la tension à ses bornes.

Réponse :

$q(t)=C \times U_C(t)$

A.4. Montrer que l’équation différentielle, dont la tension u_C aux bornes du condensateur est une solution, s’écrit sous la forme :

$\frac{d u_C}{dt}+\frac{u_C}{\tau }=\frac{ E}{\tau }$

avec τ une constante dont on précisera l’expression.

Réponse :

D’après la loi d’additivité des tensions ou loi des mailles :

$E=U_C(t)+U_R(t)$

Or $U_R(t)=R \times i$

$E=U_C(t)+R \times i$

Or $i(t)=\frac{dq(t)}{dt}$

$E=U_C(t)+R \times \frac{dq(t)}{dt}$

Or $q(t)=C \times U_C(t)$

$E=U_C(t)+R \times \frac{C \times U_C(t)}{dt}$

$E=U_C(t)+RC \times \frac{U_C(t)}{dt}$

A.5. Proposer une dénomination pour la constante τ. Montrer que cette constante a la dimension d’une durée.

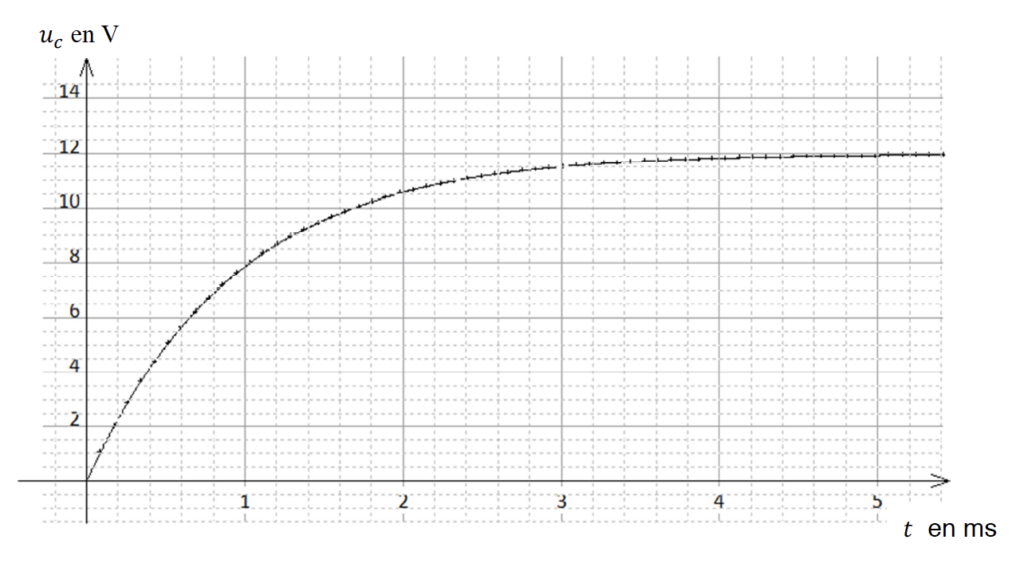
A.6. On visualise l’évolution temporelle de la tension aux bornes du condensateur. Le graphe correspondant est fourni sur l’ANNEXE 2 À RENDRE AVEC LA COPIE (p15/15).

A.6.1. Déterminer graphiquement la valeur de r. Faire apparaître soigneusement les traits de construction utiles sur le graphe de l’ANNEXE 2 À RENDRE AVEC LA COPIE (p15/15).

A.6.2. En déduire la valeur de la capacité C du condensateur, déterminée par cette méthode dans le cadre du modèle du circuit RC.

Partie B : Anatomie d’un condensateur au polycarbonate

Il existe différents types de condensateurs. Le condensateur plan est l’un des plus simples. Il est constitué de deux armatures planes de surface S séparées par un isolant d’épaisseur a. L’épaisseur des armatures est négligeable par rapport à l’épaisseur de l’isolant.

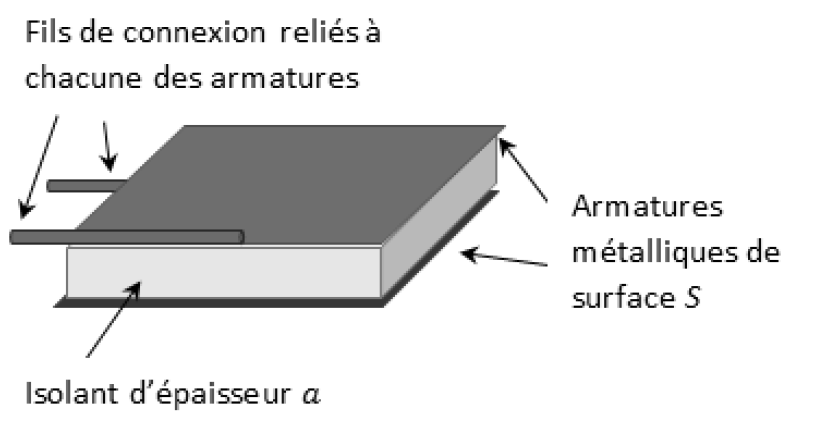
La capacité du condensateur plan est donnée par la relation :

$C_0=\frac{\epsilon \times S }{a}$

où ε est une constante qui dépend du matériau utilisé comme isolant. Pour le polycarbonate, cette valeur est = 2,57 ∙ 10^–11 F ∙ m^–1.

B.1. Décrire l’influence des caractéristiques géométriques du condensateur plan sur la valeur de sa capacité.

B.2. L’anatomie du condensateur usuel montre un empilement d’armatures métalliques avec l’isolant (ici, du polycarbonate) correspondant à une association en dérivation de n condensateurs identiques de capacité C₀ (voir la figure suivante). La capacité C de ce condensateur s’exprime par la relation C = n × C₀.

Exemples de capacités de quelques condensateurs en fonction de leurs caractéristiques géométriques :

Capacité C ± 2% (nF)	L ± 0,5 (mm)	ℎ ± 0,5 (mm)	e ± 0,5 (mm)
33,0	11,0	9,0	6,0
47,0	11,0	10,0	6,0
68,0	14,0	10,0	7,0

Source : Exxelia, fabricant de composants électroniques

Le condensateur étudié dans la partie A est fabriqué à partir d’un nombre n d’empilements de condensateurs plans élémentaires tous branchés en dérivation.

B.2.1. À l’aide des informations et schémas fournis, établir l’expression de la capacité C du condensateur en fonction des caractéristiques géométriques h, L et e, ainsi que du nombre n de condensateurs empilés.

B.2.1. La capacité du condensateur au polycarbonate valant C = 33 nF, en déduire le nombre de condensateurs élémentaires n constituant ce condensateur.

B.2.3. Le fabriquant indique que le condensateur au polycarbonate étudié dans le circuit RC est, en fait, constitué de 300 armatures métalliques. Commenter.

ANNEXE 2 À RENDRE AVEC LA COPIE (même non complétée)

Question A.6.1.

Évolution de la tension aux bornes du condensateur en fonction du temps