Aspects énergétiques des phénomènes électriques

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Autour du petit électroménager

À la maison, l’électricité est facile d’accès, semble inépuisable et nombre de ses utilisations ne peuvent pas être remplacées par une autre source d’énergie. Ces usages spécifiques représentent plus de la moitié de la consommation d’électricité des ménages, chaque foyer possédant en moyenne près d’une centaine d’appareils électriques ou électroniques.

L’efficacité énergétique de nos équipements électriques s’améliore régulièrement. Pourtant, notre consommation d’électricité́ ne cesse d’augmenter : la consommation d’électricité́ pour les petits appareils électroménagers a doublé en vingt ans.

Maitriser sa consommation d’électricité, c’est possible : il suffit souvent de bien choisir ses équipements, de bien les utiliser et de bien les entretenir.

En France, le prix du kWh électrique est de l’ordre de 15 centimes d’euros en 2019.

Sources : guide pratique « réduire sa facture d’électricité » de l’ademe.fr et edf.fr

Une famille profite de la foire de Paris pour acheter du nouveau petit électroménager.

Dans les stands, ils repèrent un grille-pain, une machine à café et une bouilloire.

La famille compte utiliser le grille-pain 5 minutes par jour tous les jours lors du petit-déjeuner.

Les deux parents prennent chacun un café par jour.

Consommations moyennes des appareils électriques d’une famille dans la cuisine.

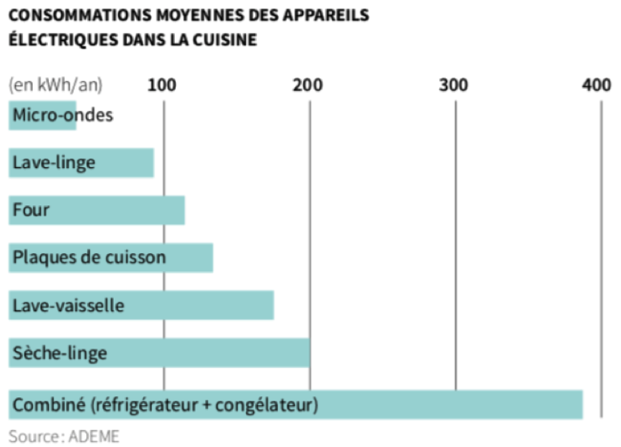
Données :

l’énergie thermique reçue par une masse m d’eau lors de la variation de sa température est proportionnelle à cette variation :

E=m.c.(T₂-T₁)

avec m la masse d’eau en kg, c la capacité thermique massique de l’eau : c = 4185 J.kg^–1.K^–1 et T₂–T₁: l’élévation de température en °C ou en K ;

1 kWh = 3,6.10⁶ J ;
masse volumique de l’eau ρ=1,0 Kg.L^-1 .

Extrait des fiches techniques des appareils

fiche technique du grille-pain	fiche technique de la bouilloire	fiche technique de la machine à café
Puissance* : 1500 W	Puissance* : 2200 W Arrêt automatique Capacité : 1,6 L	30 secondes pour faire un expresso
Prix : 29,99 euros	Prix : 19,99 euros	Prix : 99 euros

* puissance moyenne reçue par l’appareil en fonctionnement.

Partie 1 : consommation énergétique des appareils électroménagers

1.1. En utilisant vos connaissances, choisir un ordre de grandeur pour la puissance de la machine à café parmi les trois propositions suivantes :

a : 10 W ; b : 1 kW ; c : 100 kW.

La puissance de la machine à café est de l’ordre de grandeur de « b : 1 kW. »

1.2. Nommer le phénomène physique commun mis en jeu pour griller les tartines dans le grille-pain ou pour chauffer l’eau de la machine à café ou de la bouilloire.

Le phénomène physique commun mis en jeu pour griller les tartines dans le grille-pain ou pour chauffer l’eau de la machine à café ou de la bouilloire est l’effet joule.

1.3. Calculer la consommation supplémentaire d’énergie qu’apporterait l’usage de la machine à café et du grille-pain sur une année. En déduire la dépense engendrée en euros sur une année.

E=Ec+Egp

E=P_c×Δt_c+P_gp×Δt_gp

E=1.10³×30×2×365+1500×5×60×365

E=1,86.10⁸J

E=1,86.10⁸/3,6.10⁶=51,7 kWh

Le prix du kWh électrique est de l’ordre de 15 centimes d’euros

Dépense : E×0,15=51,7×0,15=7,76€

Partie 2 : rendement de la bouilloire

2.1. Pourquoi peut-on qualifier le grille-pain ou la bouilloire de convertisseurs d’énergies ?

Le grille-pain et la bouilloire utilisent de l’énergie électrique et produisent de l’énergie thermique (chaleur) : ce sont des convertisseurs d’énergie.

2.2. Définir le rendement d’un convertisseur. Expliquer sans calcul pourquoi le rendement de ces deux appareils électriques n’est pas de 100 %.

Rendement d’un convertisseur :

$\eta =\frac{E_{utile}}{E_{recue}}$

Le rendement de ces deux appareils électriques n’est pas de 100 % car il ya toujours des pertes énergétiques. Ces appareils chauffent également l’air et l’appareil, ainsi les aliments ne sont pas les seuls à être chauffé.

2.3. La bouilloire contient un volume V = 0,60 L d’eau initialement à la température T₁= 20 °C et la chauffe à la température T₂= 90 °C en 1 min 30 s. Calculer le rendement énergétique de cette bouilloire. Établir un bilan énergétique relatif à la bouilloire sous la forme d’un schéma énergétique. Commenter.

$\eta =\frac{E_{utile}}{E_{recue}}$

$\eta =\frac{m.c.(T_2-T_1)}{P\times \Delta{t}}$

$\eta =\frac{\rho .V.c.(T_2-T_1)}{P\times \Delta{t}}$

$\eta =\frac{1,0\times 0,60\times 4185\times (90-20)}{2200\times (1\times 60+30)}$

$\eta =0,89=89\%$

Bilan énergétique :

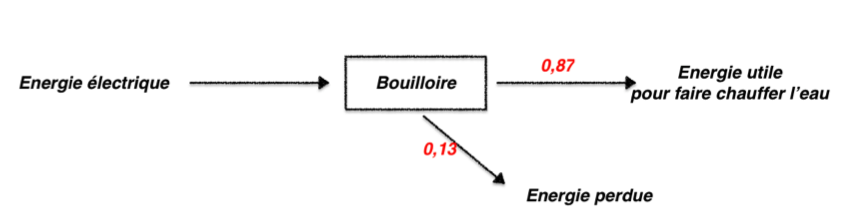
Le rendement de la bouilloire est élevé.

Partie 3 : modélisation d’une résistance chauffante au laboratoire

La résistance chauffante d’une bouilloire peut être assimilée à un conducteur ohmique.

Au laboratoire, on dispose d’un conducteur ohmique immergeable de résistance R que l’on place dans un calorimètre (récipient fermé et isolé thermiquement ; les échanges d’énergie thermique avec l‘extérieur sont ainsi très faibles). On réalise le montage représenté ci-dessous.

La résistance est en série avec un générateur de tension, de force électromotrice E, ainsi qu’un rhéostat de résistance variable R’ = 33 .

Le calorimètre est rempli d’un volume V d’eau.

Un voltmètre indique la valeur de la tension aux bornes de la résistance immergeable : U = 12,18 V.

L’ampèremètre indique que la valeur de l’intensité dans le circuit est I = 2,26 A.

On mesure également la valeur de la température de l’eau à l’aide d’un thermomètre électronique.

Initialement la température de l’eau est T₁= 28,1 °C.

On déclenche le chronomètre au moment où allume le générateur.

Les résultats sont consignés dans le tableau ci-dessous.

t (s)	60	120	180	240	300	360	420	480	540
température T de l’eau (en °C)	29,1	29,8	30,5	31,8	32,5	33,4	34,3	35,0	35,9

Le schéma du montage est représenté ci-dessous :

3.1. Calculer la valeur de la résistance R immergeable.

U=R×I

R=U/I

R=12,18/2,26

R=5,39Ω

3.2. Compléter le programme écrit en langage Python et proposé en annexe à rendre avec la copie aux lignes 2, 3 et 4 afin que celui-ci réalise le tracé de l’écart de température T–T₁ en fonction du temps exprimé en secondes.

Le graphe représentant T-T₁ en fonction du temps est donné ci-après.

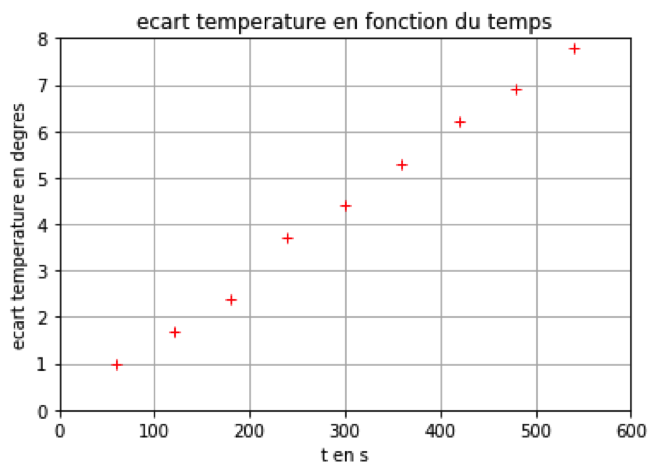
3.3. On montre que :

$\left(T-T_1\right)=\frac{R.I^2}{mc}\ .t$

avec m la masse d’eau introduite, c la capacité thermique massique de l’eau. Déterminer la valeur du volume d’eau V introduit dans le calorimètre à l’aide du graphe. On prendra R = 5,4 Ω.

Dans la ligne 2 il faut mettre les valeurs du temps consignés dans le tableau

Dans la ligne 3 il faut mettre les valeurs des écarts de températures consignées dans le tableau

Pour tracer un graphe, on utilise plt.plot( abscise , ordonnées ,’ro’,marker=’+’)

t (s)	60	120	180	240	300	360	420	480	540
température T de l’eau (en °C)	29,1	29,8	30,5	31,8	32,5	33,4	34,3	35,0	35,9
Ecarts de températures T-T₁	1	1,7	2,4	3,7	4,4	5,3	6,2	6,9	7,8

2 temps=(60, 120, 180, 240, 300, 360, 420 , 480, 540) #liste des valeurs de temps en secondes

3 ecart_T= (1, 1.7, 2.4, 3.7, 4.4, 5.3, 6.2, 6.9, 7.8)#liste des valeurs des écarts de températures en °C

4 plt.plot(temps ,ecart_T ,’ro’,marker=’+’)

Annexe à rendre avec la copie

Question 3.2.

Programme permettant de tracer T-T₁ en fonction du temps.

1 import matplotlib.pyplot as plt

2 temps= #liste des valeurs de temps en secondes

3 ecart_T= #liste des valeurs des écarts de températures en °C

4 plt.plot( , ,’ro’,marker=’+’)

5 #tracé de ecart_T en fonction du temps

6 plt.grid(True) #affiche une grille sur le graphe

7 plt.xlabel(« t en s ») #nom de l’abcisse

8 plt.ylabel(« ecart temperature en degres ») #nom de l’ordonnée

9 plt.title(« ecart temperature en fonction du temps »)

10 plt.savefig(‘graphe2.png’)

11 plt.show()