Bac Métropole Septembre 2021 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ1ME3
Sujet et corrigé
Mots-clés : énergie d’un photon ; mouvement dans un champ gravitationnel

La couronne solaire correspond à l’atmosphère du Soleil, elle est observable durant les éclipses de Soleil. C’est une couche de gaz dans laquelle les atomes sont fortement ionisés ; certains atomes peuvent perdre jusqu’à 15 électrons. L’énergie nécessaire pour arracher ces électrons est considérable et résulte de la température de la couronne solaire qui est de l’ordre de quelques millions de degrés. Le gaz de la couronne solaire est rendu visible par les rayonnements émis par ses atomes ionisés.
D’après « La couronne solaire, E. Maurice, L’Astronomie,1963 »
L’objectif de cet exercice est d’étudier le rayonnement émis par les atomes métalliques fortement ionisés de la couronne solaire, puis le mouvement de la sonde PSP (pour « Parker Solar Probe ») envoyée en 2018 pour recueillir des informations sur la couronne solaire.
1. Étude du rayonnement émis par les atomes ionisés de la couronne solaire
Les radiations caractéristiques de la couronne solaire sont dues à la formation des ions Fe9+, Fe13+, Ni14+ et Ca14+ et résultent de la transition d’un électron entre deux états d’énergie différents de chacun de ces ions.
Données :
- 1 eV = 1,6×10–19 J ;
- constante de Planck : h = 6,63×10–34J·s ;
- la valeur de la célérité c de la lumière dans le vide est supposée connue du candidat ;
- relation entre l’énergie associée à une transition énergétique et la longueur d’onde de la radiation rayonnée :
$E=\frac{ h \cdot c}{\lambda}$
- informations sur certaines radiations émises par des ions présents dans la couronne solaire :
| Ions | Longueur d’onde (en m) | Énergie associée à la transition (en eV) |
| Fe13+ | λ (Fe13+) | E (Fe13+) |
| Ca14+ | 5,694×10–7 | 2,18 |
| Fe9+ | 6,374×10–7 | 1,94 |
| Ni14+ | 6,701×10–7 | 1,85 |
Le spectre d’émission suivant a été obtenu lors de l’éclipse totale du Soleil du 29 mars 2006 en Turquie. Ce spectre montre la raie correspondant aux ions Fe13+ de la couronne solaire.

Source : Thèse de Doctorat de Cyril Bazin, 10 octobre 2013, Université Aix-Marseille
1.1. Donner la valeur de la longueur d’onde λ(Fe13+) de la radiation émise par l’ion Fe13+ en nm et en m.
Graphiquement
$$\lambda({\rm Fe}^{13+})=492\ nm$$
$$\lambda({\rm Fe}^{13+})=492\times{10}^{-9}\ m$$
$$\lambda({\rm Fe}^{13+})=4,92\times{10}^{-7}\ m$$

1.2. Préciser, en justifiant, le domaine des ondes (UV, visible, X, IR, etc.) associé à cette valeur.
$$400\ nm<\lambda_{visible}<800\ nm$$
λ(Fe13+) est donc dans le domaine des ondes visibles.
1.3. Calculer la valeur de la transition d’énergie E(Fe13+), en J puis en eV, correspondant à la raie d’émission de l’ion Fe13+.
$$E=\frac{h\times c}{\lambda}$$
$$E=\frac{6,63\times{10}^{-34}\times3,00\times{10}^8}{4,92\times{10}^{-7}}$$
$$E=4,04\times{10}^{-19}\ J$$
Or $1\ ev=1,6\times{10}^{-19}\ J$
$$E=\frac{4,04\times{10}^{-19}}{1,6\times{10}^{-19}}$$
$$E=2,53\ ev$$
2. La sonde PSP et l’assistance gravitationnelle de Vénus Données :
Données :
- masse du Soleil : MS = 1,99×1030 kg ;
- rayon du Soleil : RS = 6,96×105 km ;
- constante universelle de la gravitation : G = 6,67×10–11 m3·kg–1·s–2 .
La sonde PSP est un observatoire solaire spatial développé par l’agence spatiale américaine, la NASA, dont le lancement a eu lieu le 12 août 2018. Son objectif est d’étudier la couronne solaire en explorant une région inexplorée de l’espace située à proximité du Soleil.
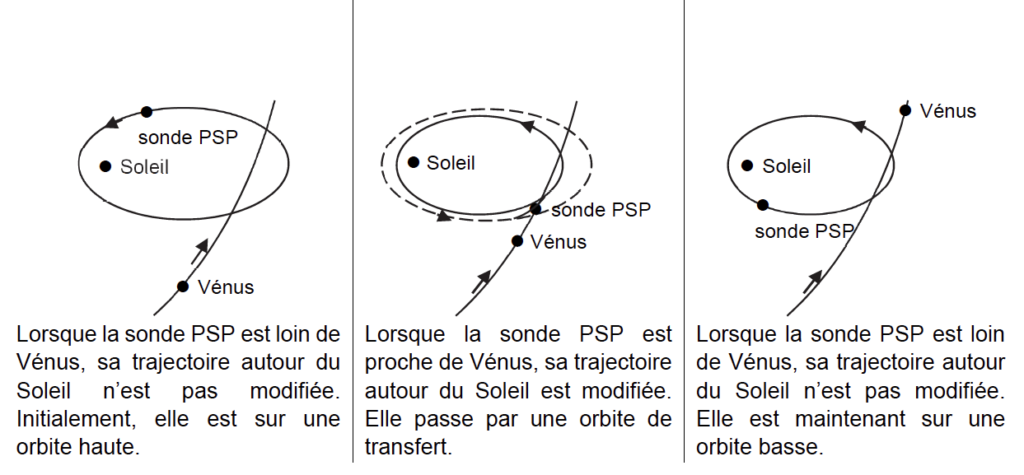
Une fois la sonde placée dans l’espace, hors du champ gravitationnel de la Terre, elle suit son voyage en direction du Soleil. Au cours de ses différentes révolutions autour du Soleil, la sonde PSP passera sept fois près de Vénus, ce qui modifiera sa trajectoire et lui permettra après chaque rencontre de se rapprocher du Soleil.
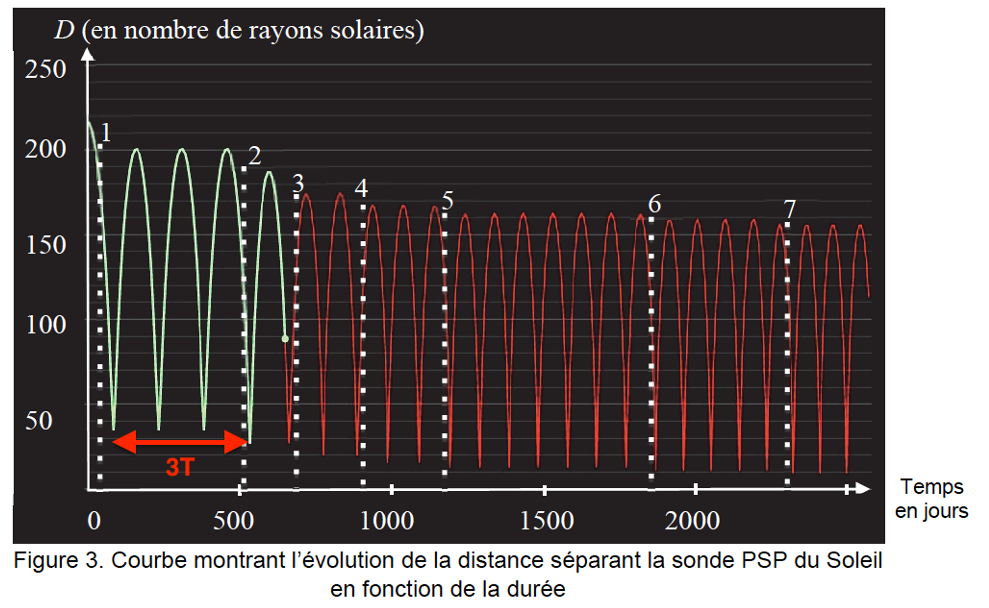
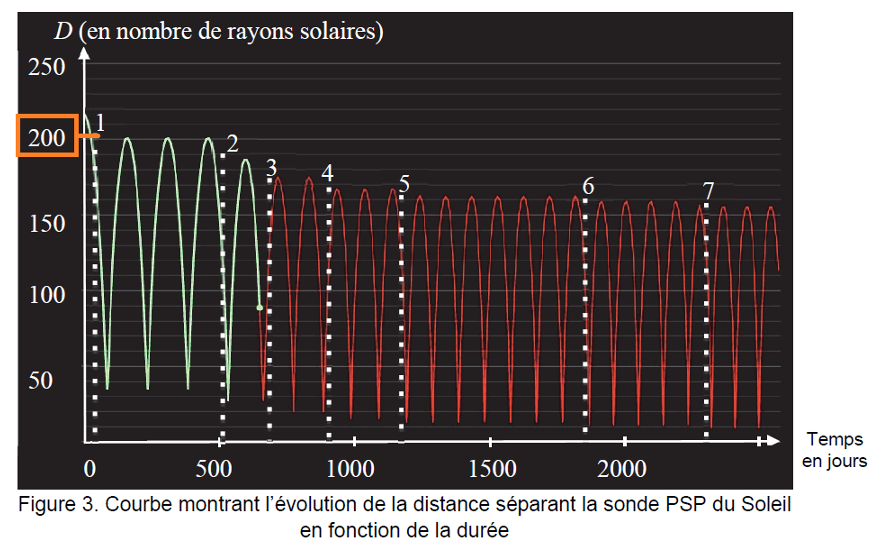
La courbe ci-après montre l’évolution de la distance séparant la sonde PSP du Soleil en fonction de la durée. La partie claire de la courbe montre la portion de trajectoire déjà parcourue au 20 mai 2020. La partie sombre présente la trajectoire modélisée par la NASA restant à parcourir par la sonde. Les sept rencontres avec Vénus sont délimitées par des traits pointillés.
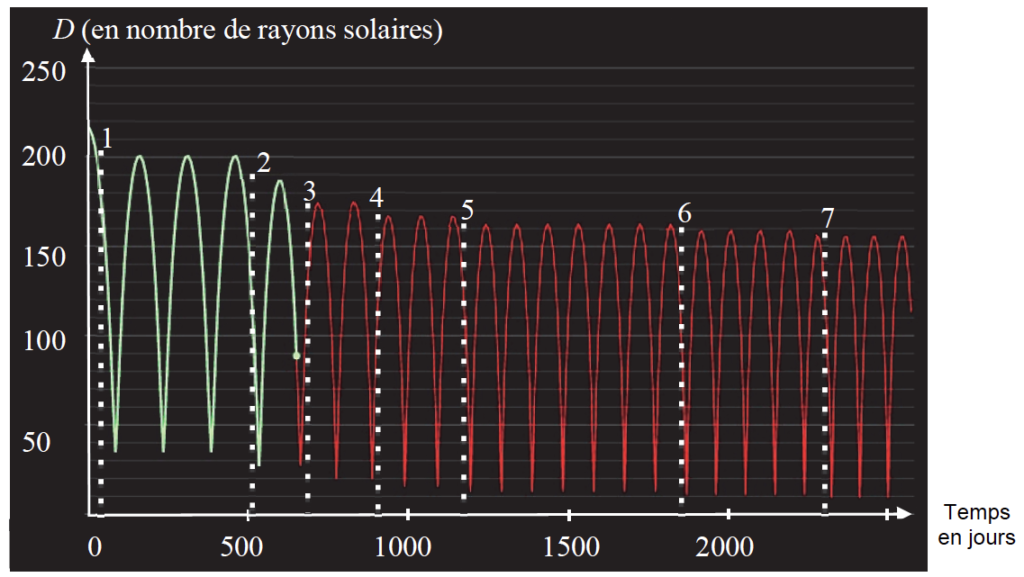
2.1. Estimer, entre la 1re et la 2e rencontre avec Vénus, les valeurs de :
- la période de révolution de la sonde PSP en jours ;
- la distance maximale entre le Soleil et la sonde PSP en km ;
- la distance minimale entre le Soleil et la sonde PSP en km.
Après la 7e rencontre, on donne les valeurs suivantes :
| Période de révolution (en jours) | Distance maximale entre le centre du Soleil et la sonde PSP (en km) | Distance minimale entre le centre du Soleil et la sonde PSP (en km) |
| 87 | 1,1×108 | 7,0×106 |
Entre la 1re et la 2e rencontre avec Vénus, la période de révolution de la sonde PSP en jours :
$$3T=490\ J$$
$$T=\frac{490}{3}=1,6\times{10}^2\ J$$
Entre la 1re et la 2e rencontre avec Vénus, la distance maximale entre le Soleil et la sonde PSP en km :
$$200\ r_S=200\times6,96\times{10}^5$$
$$200\ r_S=1,39\times{10}^8\ Km$$
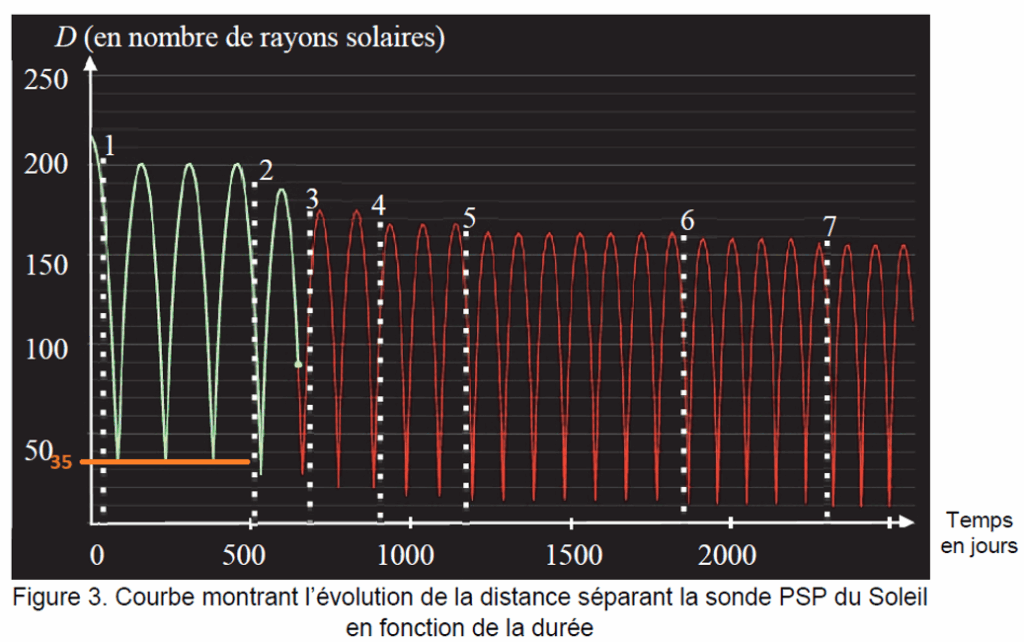
Entre la 1re et la 2e rencontre avec Vénus, la distance minimale entre le Soleil et la sonde PSP en km :
$$35\ r_S=35\times6,96\times{10}^5$$
$$35\ r_S=2,44\times{10}^7\ Km$$
2.2. Dans le cas d’un mouvement circulaire uniforme, la vitesse de la sonde PSP sur son orbite autour du Soleil a pour expression :
$v= \sqrt{\frac{G \times M_S}{R}} $
avec R le rayon de l’orbite de la sonde PSP autour du Soleil.
On note T la période de révolution de la sonde PSP autour du Soleil. Montrer que les grandeurs T et R vérifient la relation :
$\frac{T^2}{R^3}=2,97 \times 10^{-19} s^2 \cdot m^{-3}$
$$v=\sqrt{\frac{G\times M_S}{R}}$$
$$T=\frac{\text{circonference}}{\text{vitesse}}=\frac{2\pi R}{\sqrt{\frac{G\times M_S}{R}}}$$
$$T^2=\frac{4\pi^2R^2}{\frac{G\times M_S}{R}}=4\pi^2R^2\times\frac{R}{G\times M_S}$$
$$T^2=\frac{4\pi^2R^3}{G\times M_S}$$
$$\frac{T^2}{R^3}=\frac{4\pi^2}{G\times M_S}$$
$$\frac{T^2}{R^3}=\frac{4\pi^2}{6,67\times{10}^{-11}\times1,99\times{10}^{30}}$$
$$\frac{T^2}{R^3}=2,97\times{10}^{-19}\ s^2{.m}^{-3}$$
On admet que pour des trajectoires elliptiques, le rayon de l’orbite est remplacé par le demi grand-axe de l’ellipse, défini par $a=\frac{D_{max}-D_{min}}{2}$
2.3. Vérifier que les valeurs du tableau 1 sont en accord avec la relation précédente.
Calcul de $a$ avec les valeurs du tableau 1 :
$$a=\frac{1,1\times{10}^8+7\times{10}^6}{2}$$
$$a=5,85\times{10}^7\ Km$$
Calcul de $a$ avec la relation précédente :
$$\frac{T^2}{a^3}=2,97\times{10}^{-19}$$
$$\frac{a^3}{T^2}=\frac{1}{2,97\times{10}^{-19}}$$
$$a^3=\frac{T^2}{2,97\times{10}^{-19}}$$
$$a=\sqrt[3]{\frac{T^2}{2,97\times{10}^{-19}}} \text{ ou } a=\left(\frac{T^2}{2,97\times{10}^{-19}}\right)^{\frac{1}{3}}$$
$$a=\sqrt[3]{\frac{T^2}{2,97\times{10}^{-19}}}$$
$$a=5,7\times{10}^7\ Km$$
Les valeurs du tableau 1 sont en accord avec la relation précédente.
3. Estimation du record de vitesse de la sonde PSP
Les scientifiques de la NASA ont calculé avec une grande précision les positions successives de la sonde autour du Soleil au cours de son voyage. On s’intéresse au mouvement de la sonde PSP après sa septième rencontre avec la planète Vénus.
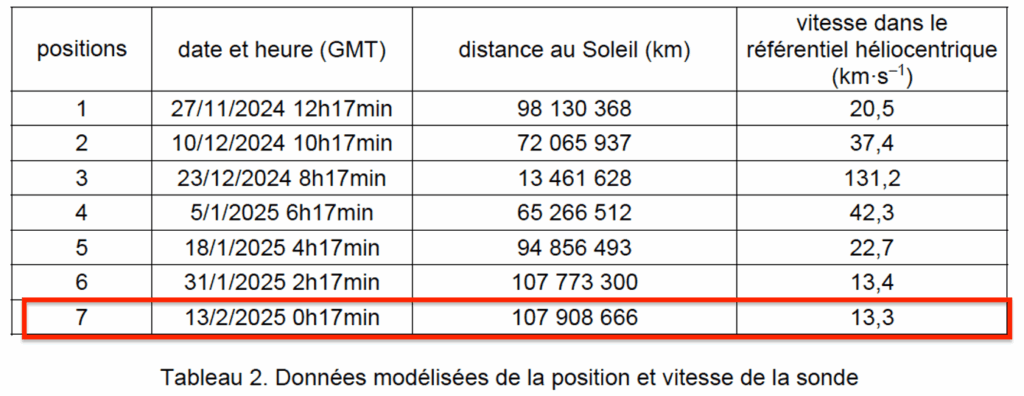
Des données modélisées et fournies par la NASA sont rassemblées ci-dessous. Elles indiquent les positions de la sonde autour du Soleil tous les 12 jours et 22 heures.
| positions | date et heure (GMT) | distance au Soleil (km) | vitesse dans le référentiel héliocentrique (km·s–1) |
| 1 | 27/11/2024 12h17min | 98 130 368 | 20,5 |
| 2 | 10/12/2024 10h17min | 72 065 937 | 37,4 |
| 3 | 23/12/2024 8h17min | 13 461 628 | 131,2 |
| 4 | 5/1/2025 6h17min | 65 266 512 | 42,3 |
| 5 | 18/1/2025 4h17min | 94 856 493 | 22,7 |
| 6 | 31/1/2025 2h17min | 107 773 300 | 13,4 |
| 7 | 13/2/2025 0h17min | 107 908 666 | 13,3 |
Tableau 2. Données modélisées de la position et vitesse de la sonde
Données :
- le référentiel héliocentrique est un référentiel défini par le centre du Soleil dont les axes pointent vers trois étoiles fixes ;
- définition du périhélie : point de la trajectoire d’un corps en orbite autour du Soleil le plus proche du Soleil ;
- définition de l’aphélie : point de la trajectoire d’un corps en orbite autour du Soleil le plus éloigné du Soleil.
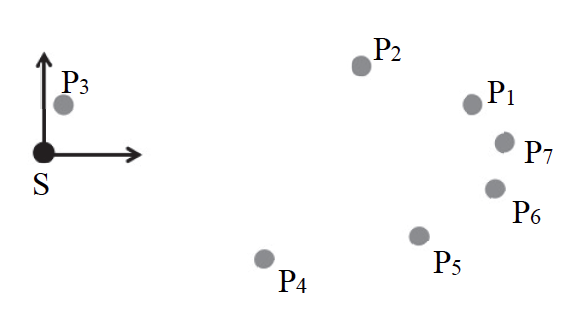
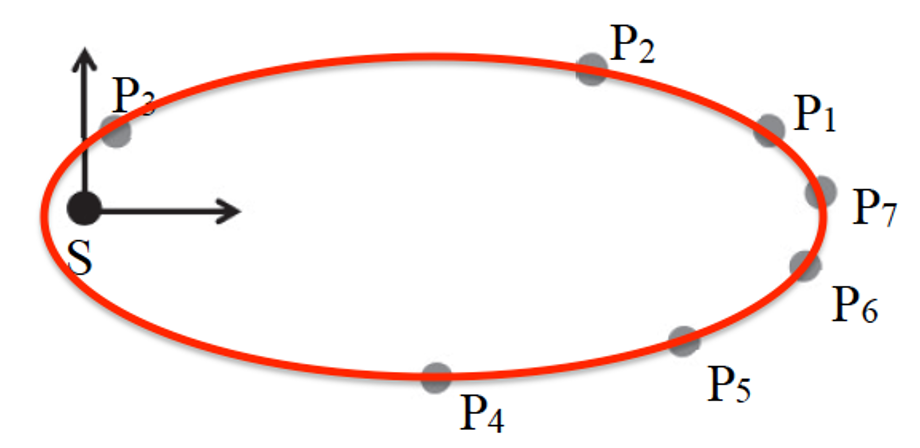
3.1. Énoncer la loi de Kepler permettant de justifier l’allure de la trajectoire de la sonde PSP autour du Soleil représentée dans la figure 4.
1ère loi de Kepler : Dans le référentiel héliocentrique, le centre de chaque planète décrit une trajectoire elliptique dont le soleil S est l’un des foyers.
L’allure de la trajectoire de la sonde PSP autour du Soleil représentée dans la figure 4 est une ellipse conformément à la 1ère loi de Kepler.
3.2. Parmi les points donnés dans le tableau 2, donner la date la plus proche à laquelle la sonde atteint l’aphélie de sa trajectoire.
On cherche la date la plus proche à laquelle la sonde atteint l’aphélie de sa trajectoire
Or « définition de l’aphélie : point de la trajectoire d’un corps en orbite autour du Soleil le plus éloigné du Soleil. »
Selon le tableau l’aphélie se situe à la position 7. Soit à la date du 13/02/2025 à 0h 17min.