Autour de Saturne

Bac Asie 2023 Sujet 1

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°23-PYCJ1JA1

EXERCICE I  ‒  AUTOUR DE SATURNE (11 points)

Illustration tirée de : starwalk.space/fr

Cet exercice a plusieurs objectifs : justifier l’utilisation d’une lunette astronomique pour observer Titan (parties A et B), étudier ses limites d’observation (partie C), puis étudier le mouvement des anneaux et de Janus (partie D).

Données :

• Diamètre apparent d’un objet et pouvoir séparateur de l’œil, document 1.

Document 1 ‒Diamètre apparent d’un objet et pouvoir séparateur

Le diamètre apparent d’un objet, noté θ, est l’angle sous lequel un objet AB est vu par un observateur (Cf. figure).

Le pouvoir séparateur de l’œil, noté ε, est la valeur minimale de l’angle sous lequel les deux points A et B peuvent être vus séparément. Pour l’œil humain, ε = 3×10^-4 rad.

• Distance moyenne Titan – Terre :  D = 1,43×10⁹ km
• Diamètre de Titan :  d = 5,2×10³ km
• Angle sous lequel est vue la lune Janus depuis la Terre :   θ_J = 1,3×10^-7 rad
• Dans tout l’exercice les angles sont suffisamment petits pour que l’on puisse faire l’approximation :  tan θ ≈ θ , avec θ en radian.

Partie A ‒ Observation de Titan à l’œil nu

1. Montrer que l’angle θ sous lequel se présente Titan depuis la Terre vaut approximativement 3,6×10^-6 rad.

Pour les angles petits :
$$\tan\left(\theta\right)\approx\theta=\frac{d}{D}$$

$$\theta=\frac{5,2\times {10}^3}{1,43\times {10}^9}$$
$$\theta=3,6\times {10}^{-6}\ rad$$

2. Justifier que Titan n’est pas observable à l’œil nu.

$$\theta<\varepsilon$$ : $\theta$ est inferieur à\ $\varepsilon$ l’angle minimal sous lequel deux points peuvent être vus séparément. Titan n’est donc pas observable à l’œil nu.

3. En déduire la valeur G_min du grossissement minimal que doit avoir un instrument d’optique, telle une lunette, pour observer Titan depuis la Terre.

$$G_{min}=\frac{\varepsilon}{\theta}$$
$$G_{min}=\frac{3\times {10}^{-4}\ }{3,6\times {10}^{-6}\ }$$
$$G_{min}=83$$

Le grossissement minimal que doit avoir un instrument d’optique pour observer Titan depuis la Terre à pour valeur 83.

Partie B ‒ Observation de Titan à l’aide d’une lunette astronomique

Une élève se rend à l’Observatoire historique de Marseille pour observer Saturne et ses satellites. Elle fait ses observations à l’aide d’une lunette astronomique dont les caractéristiques sont données ci-dessous.

Objectif : Distance focale f’_ob = 3,10 m.            Diamètre d_ob = 260 mm.

Pour l’oculaire, trois distances focales f’_oc sont possibles : 12 mm, 25 mm, 40 mm.

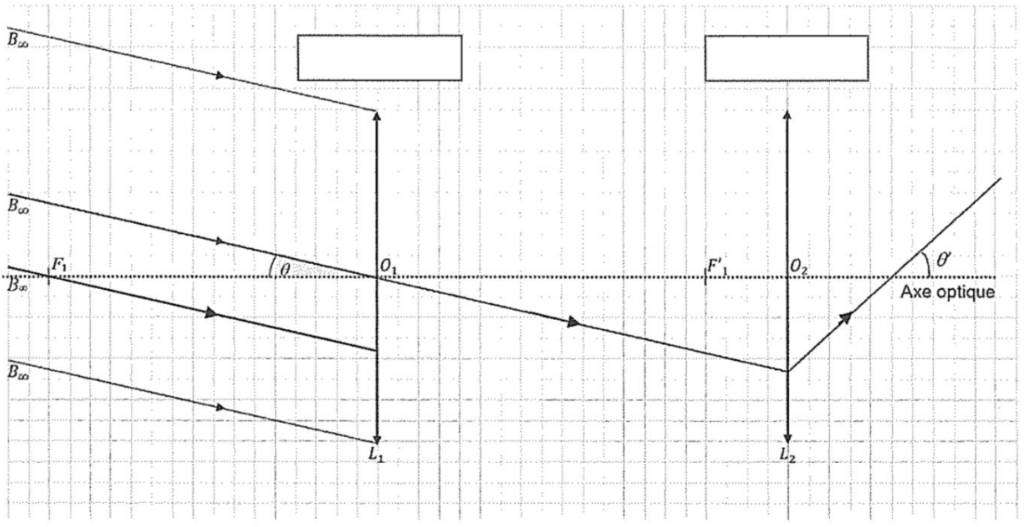
Le schéma de principe modélisant cette lunette est présenté en ANNEXE à rendre avec la copie. L’objet A_ꝏB_ꝏ observé est situé à l’infini, il est perpendiculaire à l’axe optique ; le point A_ꝏ est sur l’axe optique. Seuls quelques rayons issus de B_ꝏ sont représentés. Les angles ne sont pas à l’échelle. On rappelle qu’un système optique est dit « afocal » s’il donne d’un objet à l’infini une image à l’infini.

4. Identifier l’objectif et l’oculaire sur le schéma en ANNEXE à rendre avec la copie et positionner les foyers F₂ et F’₂ de la lentille L₂ pour obtenir une lunette afocale.

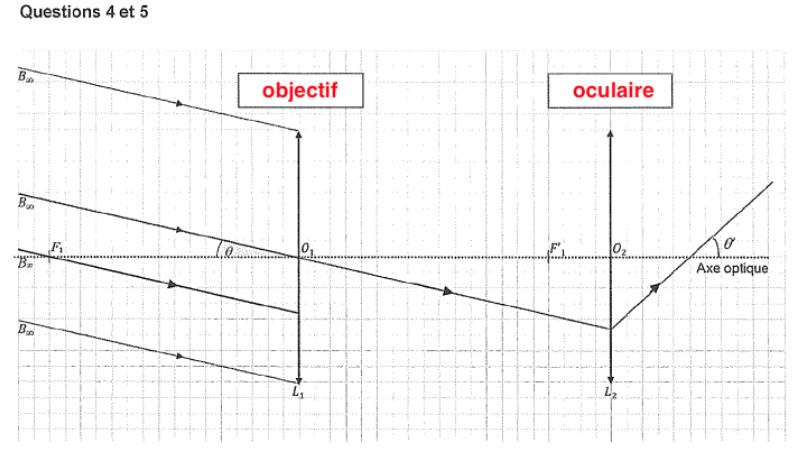
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
La lentille L₁, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le foyer image $F_1^\prime$.
Pour que la lentille L₂, donne de l’objet $A_1B_1$, une image à l’infini, il faut que celui-ci soit sur le foyer $F_2$.
Ainsi, les deux foyers $F_1^\prime$ et $F_2$ sont confondus.
De plus $OF_2=O{F\prime}_2$.

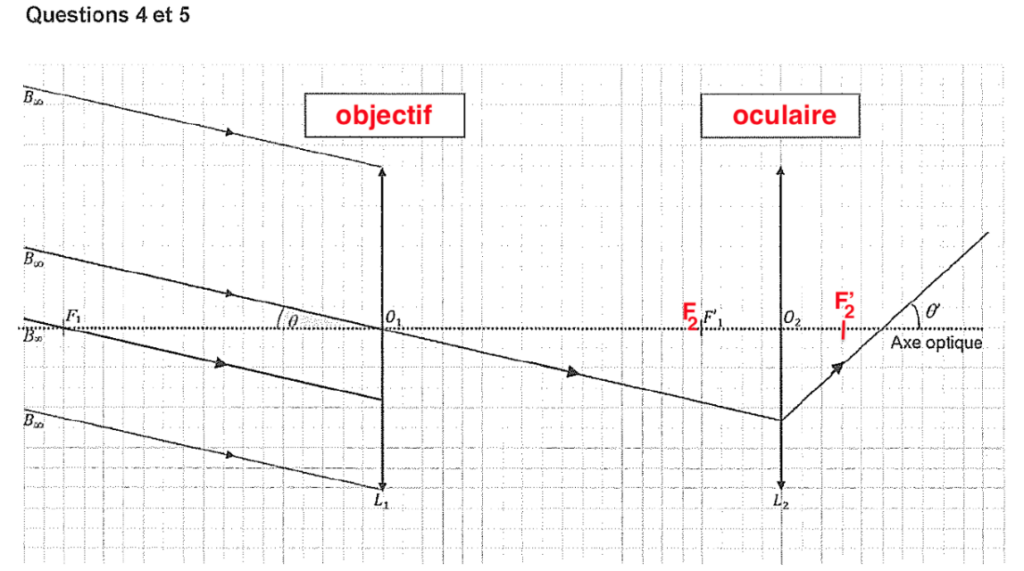
5. Construire sur le schéma en ANNEXE à rendre avec la copie la marche complète des rayons lumineux incidents issus d’un point objet B_ꝏ situé à l’infini, en faisant apparaître l’image intermédiaire B₁ donnée par la lentille L₁.

La lentille L₁, donne de l’objet $A_\infty B_\infty$, une image $A_1B_1$ sur le plan focal.
Le point B₁ est défini par l’intersection de ce rayon et le plan focal.

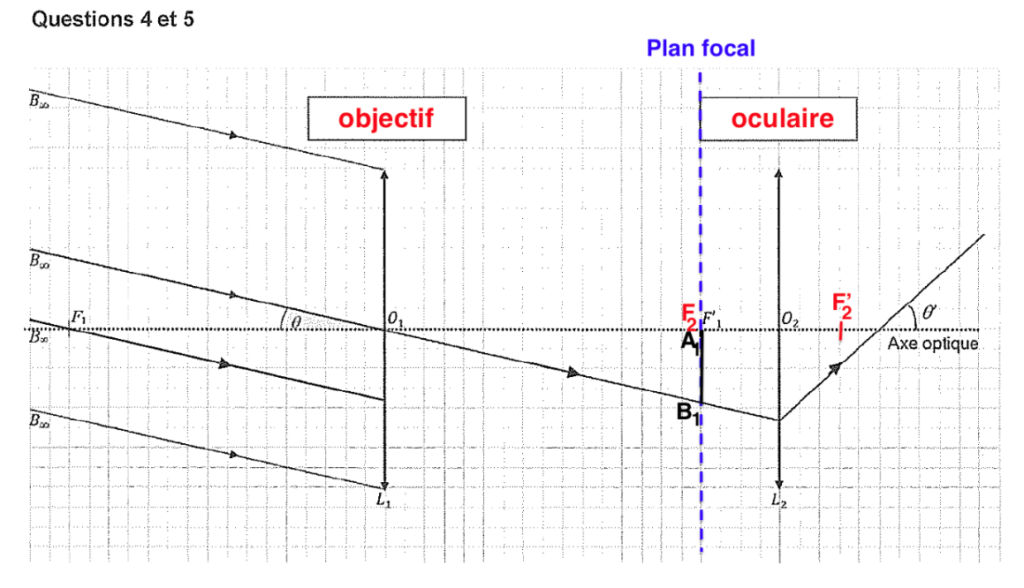
Les autres rayons sont parallèles au premier. Ils sont déviés vers le point B₁

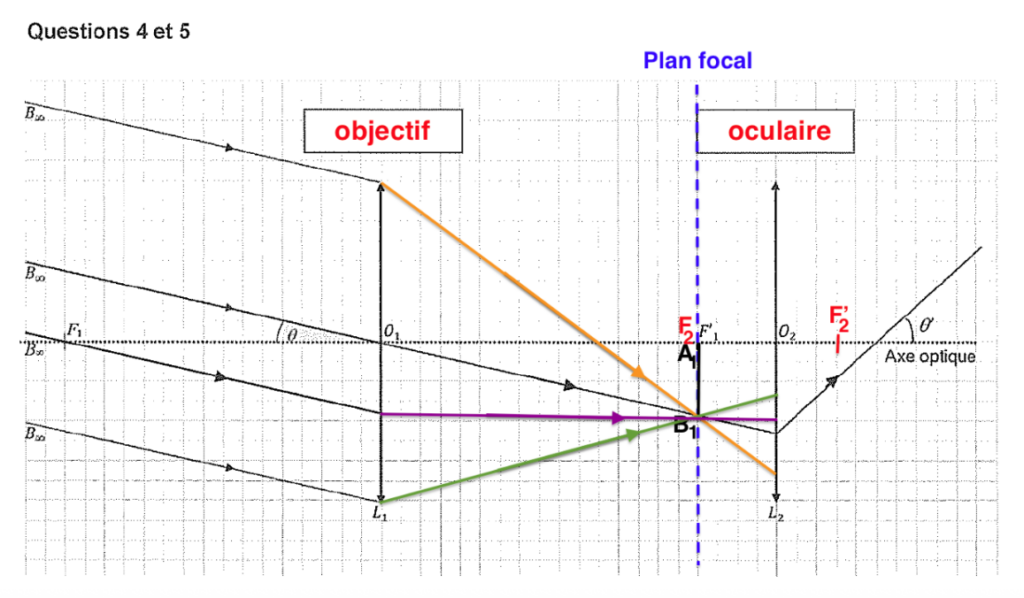
$A_1B_1$ étant sur le plan focal, il donnera une image à l’infini, tous les rayons issus de B₁, passant par la lentille L₂ seront parallèles.

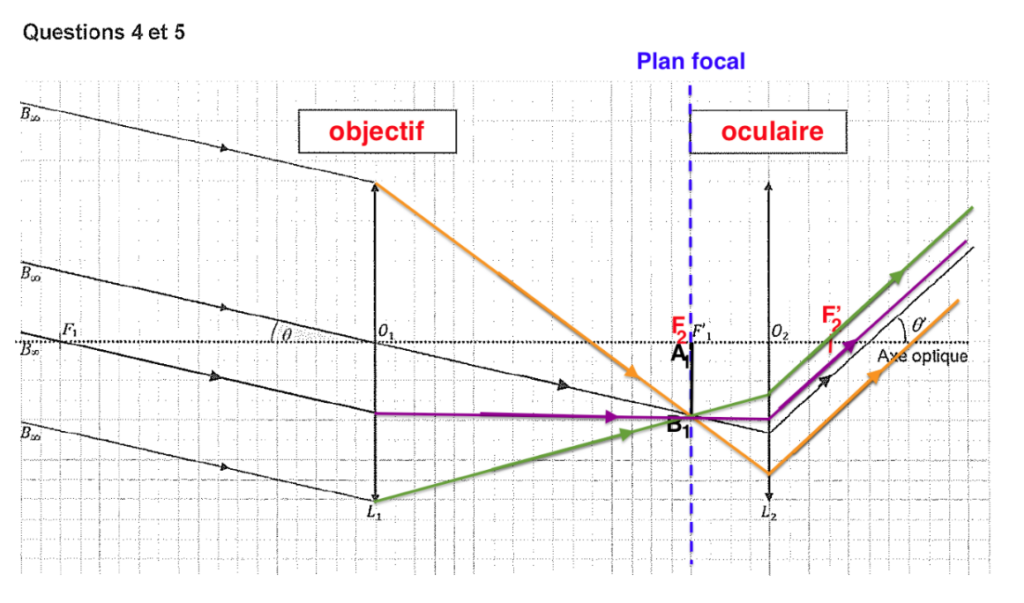
6. À partir de la définition du grossissement G, établir que dans le cas d’une lunette afocale :

$$G=\frac{f'{ob}}{f'{oc}}$$

Le grossissement G est défini par :
$$G=\frac{\theta^\prime}{\theta}$$

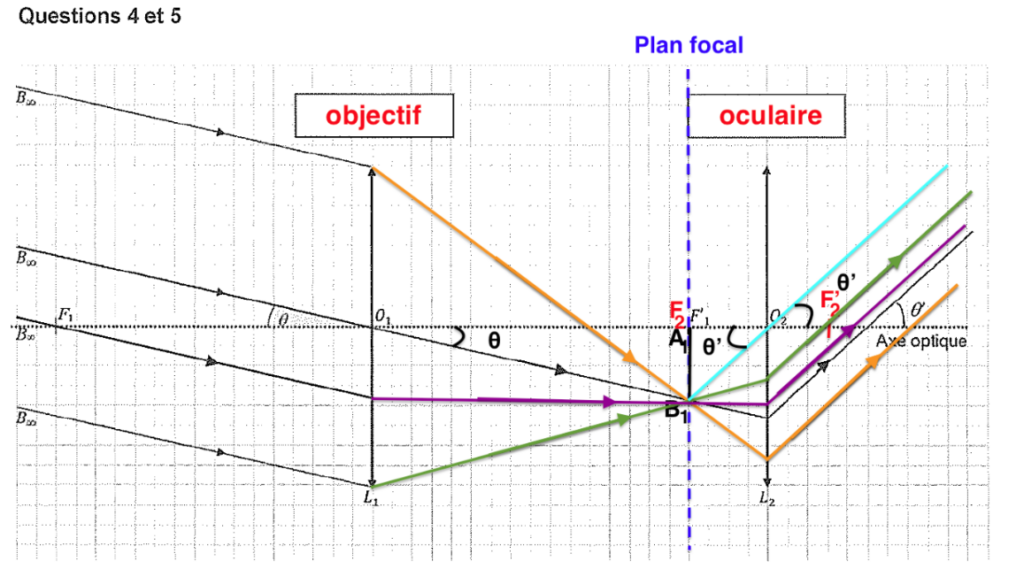
$$\tan\left(\theta\right)\approx\theta=\frac{A_1B_1}{f_{ob}^\prime}$$
$$\tan\left(\theta^\prime\right)\approx\theta^\prime=\frac{A_1B_1}{f_{oc}^\prime}$$
$$G=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_{oc}^\prime}}{\frac{A_1B_1}{f_{ob}^\prime}}=\frac{A_1B_1}{f_{oc}^\prime}\times \frac{f_{ob}^\prime}{A_1B_1}=\frac{f_{ob}^\prime}{f_{oc}^\prime}$$

7. Parmi les différents oculaires disponibles, indiquer en justifiant celui qui permet d’obtenir le grossissement maximal.

G est inversement proportionnel à $f_{oc}^\prime$. Ainsi, pour avoir un grossissement maximal, on choisit l’oculaire avec la distance focale la plus petite soit $f_{oc}^\prime=12\ mm$

8. Indiquer s’il est possible d’observer chacune des deux lunes, Titan et Janus, à l’aide de cette lunette.

$$G_{max}=\frac{f_{ob}^\prime}{f_{oc}^\prime}$$
$$G_{max}=\frac{3,10}{12\times {10}^{-3}}$$
$$G_{max}=258$$

Calculons l’angle sous lequel Titan est vu avec la lunette :
$$G=\frac{\theta^\prime}{\theta}$$
$$\theta^\prime=G\times \theta$$
$$\theta^\prime=258\times 3,6\times {10}^{-6}$$
$$\theta^\prime=9,3\times {10}^{-4}\ rad$$
$$\theta^\prime>\varepsilon$$ : $\theta$ est supérieur à\ $\varepsilon$ l’angle minimal sous lequel deux points peuvent être vus séparément. Titan est donc observable avec la lunette.

Calculons l’angle sous lequel Janus est vu avec la lunette :
$$G=\frac{\theta^\prime}{\theta_j}$$
$$\theta^\prime=G\times \theta_j$$
$$\theta^\prime=258\times 1,3\times {10}^{-7}$$
$$\theta^\prime=3,4\times {10}^{-5}\ rad$$
$$\theta^\prime<\varepsilon$$ : $\theta$ est inférieur à\ $\varepsilon$ l’angle minimal sous lequel deux points peuvent être vus séparément. Janus n’est donc pas observable avec la lunette.

9. Donner une estimation de la longueur L de la lunette de l’observatoire de Marseille en s’appuyant sur le schéma de principe de la lunette représentée en ANNEXE et sur les valeurs des distances focales.

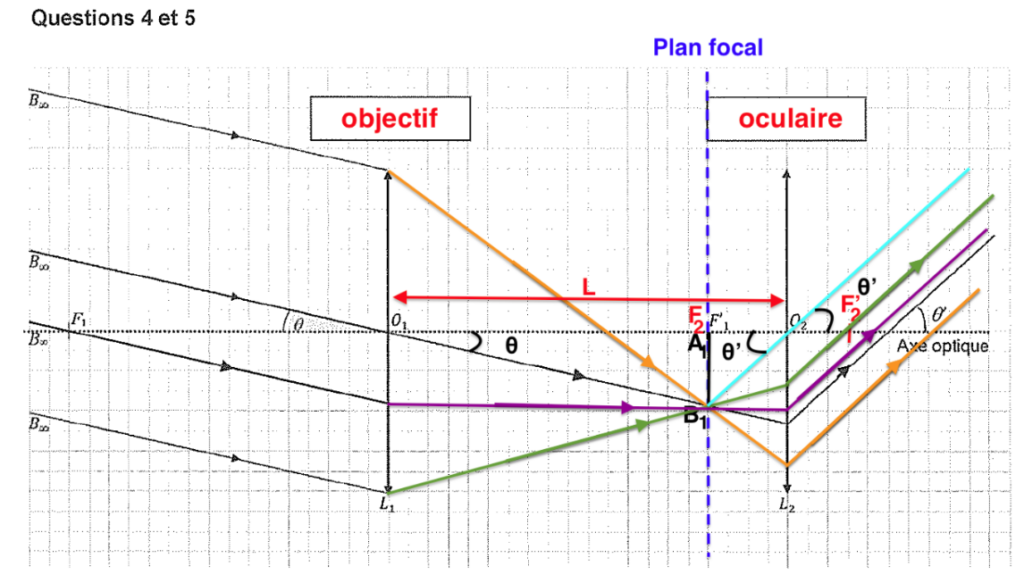
$$L=f_{ob}^\prime+f_{oc}^\prime$$

Pour $f_{oc}^\prime=12\ mm$
$$L=3,10+12\times {10}^{-3}$$
$$L=3,11m$$

Pour $f_{oc}^\prime=40\ mm$
$$L=3,10+40\times {10}^{-3}$$
$$L=3,14m$$

La longueur L de la lunette est comprise entre 3,11 m et 3,14 m.

Partie C ‒ Limites d’observation de la lunette astronomique

Le grossissement de la lunette n’est pas une donnée suffisante pour être assuré d’observer correctement Titan.

Tache d’Airy

Document 2 ‒ Pouvoir de résolution d’un instrument d’optique

Le pouvoir de résolution est lié à la capacité à discerner les détails à travers un système optique (microscope, télescope, lunette, œil…). Il est caractérisé par un angle a.

Pour une lunette, il a pour expression :

$$\alpha=\frac{1,22\times\lambda}{d_{ob}}$$

où l est la longueur d’onde du faisceau incident et d_ob le diamètre de l’objectif.

La lunette astronomique permet de distinguer deux points à condition que l’écart angulaire θ’ entre ces deux points soit supérieur ou égal à l’angle a (voir figures ci-dessous)

10. Nommer le phénomène physique qui limite le pouvoir de résolution de la lunette.

Le phénomène physique qui limite le pouvoir de résolution est la diffraction.

Un critère retenu pour voir correctement Titan est de pouvoir distinguer ses pôles, repérés par les points A et B (schéma ci-contre).

11. Pour la longueur d’onde du visible λ = 550 nm et pour un grossissement G = 260, vérifier que la lunette permet d’observer Titan correctement.

$$\alpha=\frac{1,22\times \lambda}{d_{ob}}$$
$$\alpha=\frac{1,22\times 500\times {10}^{-9}}{260\times {10}^{-3}}$$
$$\alpha=2,34\times {10}^{-6}\ rad$$

Pour un grossissement $G=260$, calculons l’angle sous lequel Titan est vu avec la lunette :
$$G=\frac{\theta^\prime}{\theta}$$
$$\theta^\prime=G\times \theta$$
$$\theta^\prime=260\times 3,6\times {10}^{-6}$$
$$\theta^\prime=9,4\times {10}^{-4}\ rad$$

$$\theta^\prime>\alpha$$ : les deux points peuvent être discernés : la lunette permet d’observer Titan correctement.

12. Expliquer pourquoi il est préférable d’utiliser des lunettes avec un objectif ayant un grand diamètre d’ouverture.

$$\alpha=\frac{1,22\times \lambda}{d_{ob}}$$
α est inversement proportionnel au diamètre d’ouverture d_ob. Plus d_ob est grand, plus α est petit et plus il est possible de distinguer deux points avec une lunette astronomique.

Partie D ‒ Autour de Saturne

Les anneaux de Saturne semblent continus depuis la Terre. En réalité, ils sont constitués de morceaux de glace et de poussières dont la taille maximale est de l’ordre de quelques centaines de mètres. Chacun de ces morceaux, tout comme les lunes en orbite autour de Saturne, obéissent aux lois du mouvement d’un satellite dans un champ de gravitation.

Données

• Rayon de Saturne :  R_S = 58,2×10³ km
• Rayon intérieur du premier anneau : r_int = 6,69×10⁴ km
• Rayon extérieur du premier anneau : r_ext = 7,45×10⁴ km
• Rayon extérieur du dernier anneau : R_ext = 1,36×10⁵ km
• Rayon de l’orbite de Janus : R_J = 1,51×10⁵ km
• Constante de gravitation universelle : G = 6,67×10^-11 m³·km^-1·s^-2

La vitesse v, constante, d’un satellite de masse m en orbite circulaire autour de Saturne est donnée par la relation :

$v=\sqrt{\frac{G\times M_S}{r}}$     (relation 1)

Où r est le rayon constant de l’orbite du satellite et M_S la masse de Saturne.

13. Retrouver la relation 1 en utilisant la deuxième loi de Newton et la loi d’interaction gravitationnelle.

$$\overrightarrow{F_{S/satellite}}=G\ .\frac{M_S\times M_{satellite\ }}{r^2}{\overrightarrow{u}}_N$$

Système : satellite de Saturne
Référentiel : saturnocentrique supposé galiléen.

D’après la 2nd loi de Newton :

$$\Sigma\overrightarrow{F_{ext}}=M_{satellite\ }\overrightarrow{a}$$

$$\overrightarrow{F_{S/satellite}}=M_{satellite\ }\overrightarrow{a}$$

$$G\ \times \frac{M_S\times M_{satellite\ }}{r^2}{\overrightarrow{u}}N=M{satellite\ }\overrightarrow{a}$$

$$\overrightarrow{a}=G\ \times \frac{M_S}{r^2}{\overrightarrow{u}}_N$$

 
Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme:
$$\overrightarrow{a}=\frac{v^2}{r}{\overrightarrow{u}}_N+\frac{dv}{dt}{\overrightarrow{u}}_T$$

L’accélération étant unique, par identification :
$$\frac{v^2}{r}=G\ \times \frac{M_S}{r^2}$$

$$v^2=G\ \times \frac{M_S}{r}$$
$$v=\sqrt{G\ \times \frac{M_S}{r}}$$
$$v=\sqrt{\frac{{G\ \times M}_S}{r}}$$

14. Montrer que l’expression de la vitesse du satellite permet de retrouver la troisième loi de Kepler qui relie la période T du satellite au rayon r de son orbite :  T² = k r³  avec $ k=\frac{4\pi^2}{G\times M_S}$

La période de révolution est :
$$T=\frac{Périmètre\ d’un \ cercle}{vitesse}$$
$$T=\frac{2\pi r}{v}=\frac{2\pi r}{\sqrt{\frac{{G\ \times M}_S}{r}}}=2\pi r\sqrt{\frac{r}{{G\ .M}_S}}$$
$$T=2\pi\sqrt{r^2\frac{r}{{G\times M}_S}}$$
$$T=2\pi\sqrt{\frac{r^3}{{G\ \times M}_S}}$$
$$T^2=\left(2\pi\sqrt{\frac{r^3}{{G\ \times M}_S}}\right)^2$$
$$T^2=4\pi^2{\sqrt{\frac{r^3}{{G\ \times M}_S}}}^2$$
$$T^2=4\pi^2\frac{r^3}{{G\ \times M}_S}$$
$$T^2=\frac{4\pi^2}{{G\ \times M}_S}\times r^3$$
$$T^2=k \times r^3$$

Avec
$$k=\frac{4\pi^2}{{G\ \times M}_S}$$
L’expression de la vitesse du satellite permet de retrouver la troisième loi de Kepler.

15. Déterminer la masse de Saturne sachant que la période de révolution de Janus est de 17h.

$${T_J}^2=\frac{4\pi^2}{{G\ \times M}_S}\times {R_J}^3$$
$${T_J}^2\times M_S=\frac{4\pi^2}{G}\times {R_J}^3$$
$$M_S=\frac{4\pi^2}{G\times {T_J}^2}\times {R_J}^3$$
$$M_S=\frac{4\pi^2}{6,67\times {10}^{-11}\times \left(17\times 60\times 60\right)^2}\times \left(1,51\times {10}^5\times {10}^3\right)^3$$
$$M_S=5,4\times {10}^{26}\ kg$$

16. Justifier qualitativement que tous les corps du premier anneau ne tournent pas à la même vitesse autour de Saturne.

Le premier anneau est limité par un rayon intérieur et un rayon extérieur.
Or la vitesse dépend du rayon
$$\mathbf{v}=\sqrt{\frac{{\mathbf{G}\ \times \mathbf{M}}_\mathbf{S}}{\mathbf{r}}}$$
Tous les corps du premier anneau n’ayant pas le même rayon d’orbite, ne tournent pas à la même vitesse autour de Saturne.

17. Déterminer le nombre de tours effectués par la bordure interne du premier anneau, située à la distance r_int, pendant que la bordure externe du dernier anneau, située à R_ext, réalise un tour complet.

Comparons les périodes de révolutions d’un corps tournant sur le rayon intérieur du premier anneau et d’un corps tournant sur le rayon extérieur du dernier anneau.

D’après la question 14. :
$$T=2\pi\sqrt{\frac{r^3}{{G\ \times M}S}}$$
$$T{ext}=2\pi\sqrt{\frac{{R_{ext}}^3}{{G\ \times M}S}}$$
$$T{int}=2\pi\sqrt{\frac{{r_{int}}^3}{{G\ \times M}_S}}$$

$$\frac{T_{ext}}{T_{int}}=\frac{2\pi\sqrt{\frac{{R_{ext}}^3}{{G\ \times M}S}}}{2\pi\sqrt{\frac{{r{int}}^3}{{G\ \times M}S}}}$$
$$\frac{T{ext}}{T_{int}}=\sqrt{\frac{\frac{{R_{ext}}^3}{{G\ \times M}S}}{\frac{{r{int}}^3}{{G\ \times M}S}}}$$
$$\frac{T{ext}}{T_{int}}=\sqrt{\frac{{R_{ext}}^3}{{G\ \times M}S}\times \frac{{G\ \times M}S}{{r{int}}^3}}$$
$$\frac{T{ext}}{T_{int}}=\sqrt{\frac{{R_{ext}}^3}{{r_{int}}^3}}$$
$$\frac{T_{ext}}{T_{int}}=\sqrt{\left(\frac{R_{ext}}{r_{int}}\right)^3}$$
$$\frac{T_{ext}}{T_{int}}=\sqrt{\left(\frac{1,36\times {10}^5\times {10}^3}{6,69\times {10}^4\times {10}^3}\right)^3}$$
$$\frac{T_{ext}}{T_{int}}=2,90$$

La période de révolution de la bordure du premier anneau est environ 3 fois supérieure à La période de révolution de la bordure externe effectue.

Ainsi, la bordure du premier anneau effectue environ 3 tours pendant que la bordure externe effectue un tour complet.

ANNEXE A RENDRE AVEC LA COPIE

EXERCICE I

Questions 4 et 5