Enseignement scientifique première
Durée 1h – 10 points – Thème « Son et musique, porteurs d’information »
[latexpage]
Partie 1. Masse et fréquence
On dispose de trois marteaux M1, M2 et M3 de masses respectives m1 = 0,24 kg, m2 = 0,48 kg et m3 = 1,44 kg.
L’expérience consiste à les laisser tomber sur une enclume. Un logiciel d’acquisition enregistre le signal sonore émis.
On désigne respectivement par f1, f2 et f3 les fréquences fondamentales des sons émis par les marteaux M1, M2 et M3 lors de l’expérience.
Document 1 : Spectres des fréquences des sons émis lors de la chute des marteaux
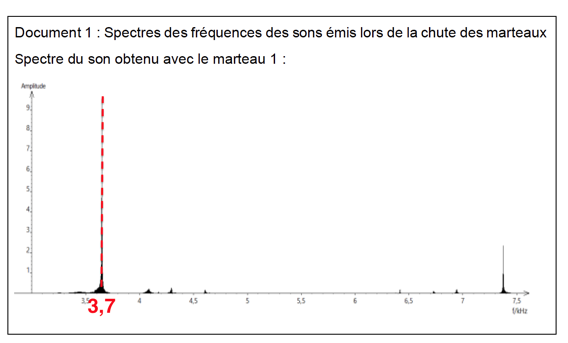
Spectre du son obtenu avec le marteau 1 :
Spectre du son obtenu avec le marteau 2 :

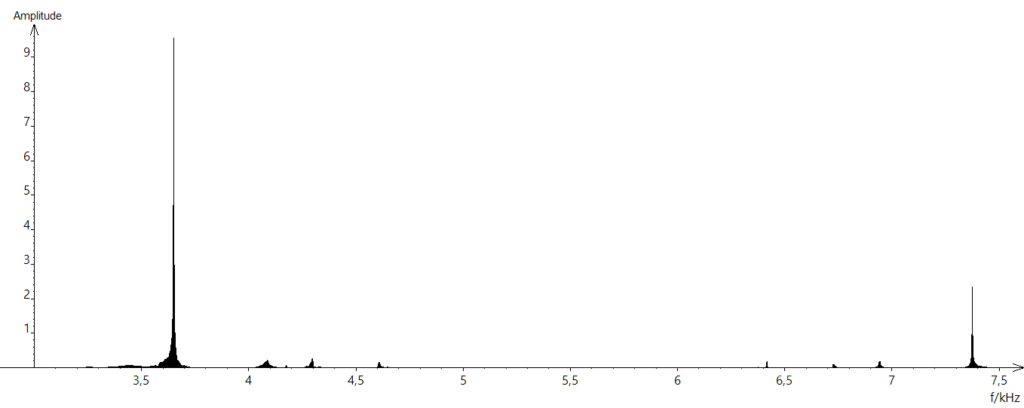
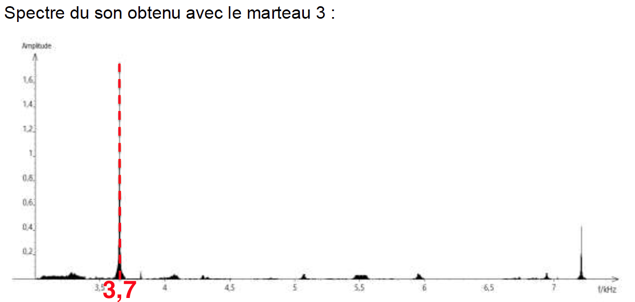
Spectre du son obtenu avec le marteau 3 :
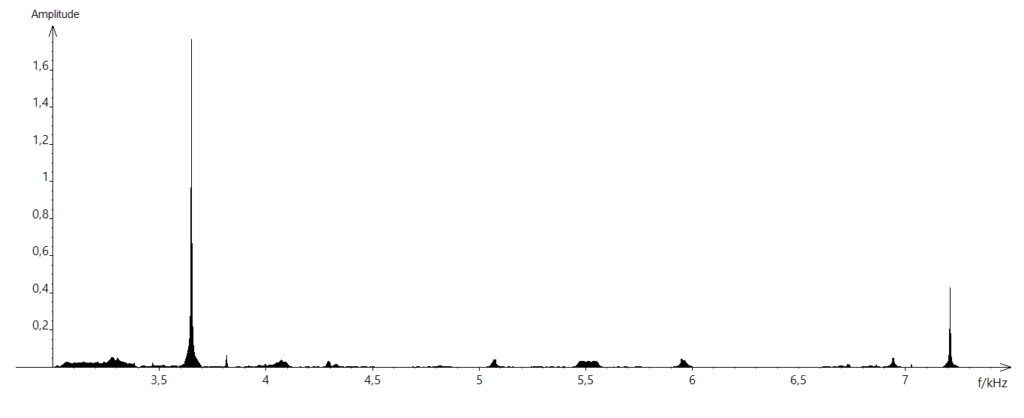
- Lire sur le document 1 les fréquences fondamentales f1, f2, et f3 des sons émis lors de l’expérience et noter leurs valeurs sur la copie.
f1=3,7 khz
f2=3,7 khz
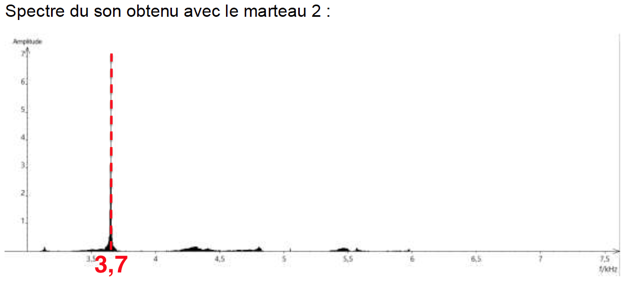
f3=3,7 khz
2. Comparer ces fréquences. La masse du marteau influe-t-elle sur la fréquence fondamentale du son émis ?
Ces fréquences sont identiques. On en déduit que La masse du marteau n’influe pas sur la fréquence fondamentale du son émis.
Partie 2. Construction d’une gamme
On souhaite construire une gamme musicale en harmonie avec la note obtenue en tapant sur l’enclume de la partie 1. On admet que cette fréquence vaut environ 3600 Hz.
3. Cette note, jugée trop aigüe, doit être diminuée de plusieurs octaves pour obtenir une fréquence proche de 440 Hz, qui correspond à la fréquence du La3 servant communément de référence. Combien d’octaves séparent la note obtenue en tapant sur l’enclume et le La3 ?
\[\frac{3600}{440}\approx 8\]
Huit octaves séparent la note obtenue en tapant sur l’enclume et le La3.
4. Dans une gamme de douze notes au tempérament égal (aussi appelée gamme tempérée), la fréquence de chaque note est obtenue en multipliant la fréquence de la note précédente par la racine douzième de deux, notée 12√2 ou 21/12.
| 𝐹 ← ⋯ Pour i allant de … à … Afficher F 𝐹 ← ⋯ Fin Pour |
4-a- Recopier et compléter l’algorithme ci-dessous pour qu’il permette de construire la gamme de douze notes au tempérament égal à partir de la note de fréquence F = f0.
| 𝐹 ← f0 Pour i allant de … à … Afficher F 𝐹 ← F×12√2 Fin Pour |
4-b- Donner la valeur de B dans le tableau des fréquences ci-dessous :
| Note 0 | Note 1 | Note 2 | Note 3 | Note 4 | Note 5 | Note 6 | Note 7 | Note 8 | Note 9 | Note 10 | Note 11 | Note 11 | |
| Fréquence 𝑓 (Hz) | 455 =𝑓0 | 482 | 511 | 541 | 573 | 607 | A | 682 | 723 | 765 | 811 | 859 | 910 |
| Rapport 𝑓/𝑓0 | 1 | 21/12 | 22/12 | 23/12 | 24/12 | 25/12 | B | 27/12 | 28/12 | 29/12 | 210/12 | 211/12 | 2 |
\[B=2^{\frac{6}{12}}\]
4-c- Expliquer pourquoi A2 = 682 × 607 puis donner la valeur de A.
D’une part :
\[A=607\times 2^{\frac{1}{12}}\]
D’autre part :
\[682=A\times 2^{\frac{1}{12}}\]
\[A\times 2^{\frac{1}{12}}=682\]
\[A=\frac{682}{2^{\frac{1}{12}}}\]
D’où :
A2=A×A
A\[^2=607\times 2^{\frac{1}{12}}\times \frac{682}{2^{\frac{1}{12}}}\]
\[A^2=607\times 682\]
\[A=\sqrt{607\times 682}\]
A=643
5. On rappelle que la quinte juste introduite pour construire les gammes de Pythagore est exactement 3/2.
Déterminer la note de la gamme qui forme avec la note 0 l’intervalle le plus proche de la quinte juste.
\[f=\frac{3}{2}\times f_0}\]
\[f=\frac{3}{2}\times 455}\]
f=682 Hz
| Note 0 | Note 1 | Note 2 | Note 3 | Note 4 | Note 5 | Note 6 | Note 7 | Note 8 | Note 9 | Note 10 | Note 11 | Note 11 | |
| Fréquence 𝑓 (Hz) | 455 =𝑓0 | 482 | 511 | 541 | 573 | 607 | A | 682 | 723 | 765 | 811 | 859 | 910 |
| Rapport 𝑓/𝑓0 | 1 | 21/12 | 22/12 | 23/12 | 24/12 | 25/12 | B | 27/12 | 28/12 | 29/12 | 210/12 | 211/12 | 2 |
La note de la gamme qui forme avec la note 0 l’intervalle le plus proche de la quinte juste est la note 7 de fréquence 682 Hz.
