Ballon sonde

E3C2 – 10 points – Durée 1h – calculatrice autorisée

Le 17 mars 1898, le premier ballon-sonde météorologique français était lancé depuis l’observatoire de Trappes, en région parisienne. Il emportait, dans un panier d’osier, un « météorographe », destiné à enregistrer la pression et la température en altitude. Aujourd’hui, les ballons-sondes sont toujours utilisés (figure 1). Ces radiosondages fournissent des informations sur l’état des premières couches de l’atmosphère (troposphère et stratosphère).

D’après : meteofrance.com 16/03/2018

Figure 1 : lâcher de ballon automatique © Météo-France, Pascal Taburet

Dans le cadre d’un atelier scientifique, des lycéens ont conçu un ballon-sonde constitué :

d’une enveloppe fermée remplie d’hélium ;
d’une nacelle contenant des appareils de mesure et un parachute.

Lors du lâcher, le ballon-sonde communique avec une station au sol. Des mesures de pression, température, position sont récoltées au cours de l’ascension.

L’objectif de cet exercice est de justifier le choix de valeur de la fréquence de télécommunication et de confronter certaines mesures réalisées à des modèles physiques.

Données :

la valeur de la célérité c des ondes électromagnétiques dans le vide ou dans l’air est supposée connue des candidats
masse(enveloppe) = 3,2 x 10² g ;
masse(nacelle)= 3,6 kg ;
masse(hélium)= 7,0 x 10² g ;
intensité du champ de pesanteur : g = 9,81 m.s^-2 ;
pression atmosphérique au niveau du sol : P₀ = 1,0 x 10³ hPa ;
volume initial du ballon : V₀ = 4,0 m³ ;
volume du ballon juste avant éclatement : V_max = 51 m³.

choix technique pour la télécommunication

Pour éviter les interférences avec d’autres systèmes, les lycéens doivent respecter les normes en vigueur. Leur ballon-sonde doit émettre des ondes électromagnétiques dans le domaine radioélectrique UHF (Ultra Hautes Fréquences), que l’union internationale des télécommunications a attribué au service de la météorologie.

Les lycéens ont choisi de régler la valeur de la fréquence d’émission de leur ballon-sonde à f = 403,2 MHz.

Figure 2 : différents domaines du spectre des ondes électromagnétiques

1.1. Citer un autre type d’ondes que les ondes électromagnétiques. En donner un exemple.

Les ondes mécaniques sont un autre type d’onde. Le son est un exemple d’onde mécanique

1.2. Exprimer la relation entre célérité c, longueur d’onde λ et fréquence f.

$\lambda =\frac{c}{f}$

1.3. Déterminer la valeur de la longueur d’onde des ondes émises par le ballon-sonde. Commenter le choix effectué par les lycéens par rapport aux normes de télécommunication.

$\lambda =\frac{c}{f}$

$\lambda =\frac{3,00.10^8}{403,2.10^6}=0,74\ m$

D’après le texte : « Leur ballon-sonde doit émettre des ondes électromagnétiques dans le domaine radioélectrique UHF (Ultra Hautes Fréquences), que l’union internationale des télécommunications a attribué au service de la météorologie »

Sur la figure 2 :

UHF est un domaine compris entre 10 cm et 1 m. La valeur choisie est comprise dans cet intervalle.

2. Décollage du ballon-sonde

On considère le ballon juste après le décollage, étudié dans le référentiel terrestre supposé galiléen. On néglige les frottements exercés par l’air.

Le système {ballon + nacelle + hélium} est soumis à deux forces :

son poids, noté ;
la poussée d’Archimède, notée , verticale, dirigée vers le haut telle que sa norme F = 50 N.

2.1. Calculer la valeur de la masse m totale du système étudié.

Système {ballon + nacelle + hélium}

$m_{systeme}=m_{ballon}+m_{nacelle}+m_{hélium}$

$m_{systeme}=3,2.10^2+3,6.10^3+ 7,0.10^2$

$m_{systeme}=4,62.10^3g=4,62\ Kg$

2.2. Calculer la valeur du poids du système {ballon + nacelle + hélium}.

$P_{systeme}=m_{systeme}\times g$

$P_{systeme}=4,62\times 9,81=45,3\ N$

2.3. Représenter les forces exercées sur le système {ballon + nacelle + hélium} modélisé par un point matériel noté S (échelle : 10 N ↔ 1 cm).

F : la poussée d’Archimède, elle est verticale et dirigée vers le haut.

P : le poids, elle est verticale et dirigée vers le bas

échelle : 10 N ↔ 1 cm

F=50 N soit 5 cm

P=45,3 N soit 4,5 cm

2.4. En déduire le vecteur représentant la somme des forces appliquées sur le système et donner les caractéristiques de ce vecteur (direction, sens, norme).

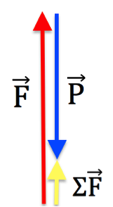
La somme des forces est verticale et dirigée vers le haut . Sa norme se mesure sur le schéma : 0,5 cm soit 5N (échelle : 10 N ↔ 1 cm).

Le ballon possède une trajectoire verticale ascendante. Les lycéens ont calculé la vitesse du ballon-sonde à partir des mesures de positions. La vitesse est V₁ = 1,1 m.s^-1à t₁ = 1,0 s et V₃ = 3,2 m.s^-1 à t₃ = 3,0 s.

2.5. Calculer la variation de la valeur de la vitesse entre les instants t₁ et t₃.

$\Delta v=v_{3}-v_{1}$

$\Delta v=3,2-1,1=2,1m.s^{-1}$

2.6. Montrer que cette variation est cohérente avec les caractéristiques de la somme des forces appliquées sur le système.

$\Sigma \vec{F}=m\times \frac{\Delta \vec{v}}{\Delta t}}$

Les deux vecteurs ont la même direction et le même sens. Ainsi la somme des forces est verticale et dirigée vers le haut.

Calculons la norme :

$\Sigma F=m\times \frac{\Delta v}{\Delta t}}$

$\Sigma F=4,62\times \frac{2,1}{3,0-1,0}}=4,9N$

Cette valeur est proche de la valeur trouvée à la question 2.4

Ainsi cette variation cohérente avec les caractéristiques de la somme des forces appliquées sur le système.

3. Éclatement

Dans cette partie, on considère que l’enveloppe du ballon-sonde est parfaitement souple et extensible de sorte que la pression de l’hélium à l’intérieur est constamment égale à la pression atmosphérique.

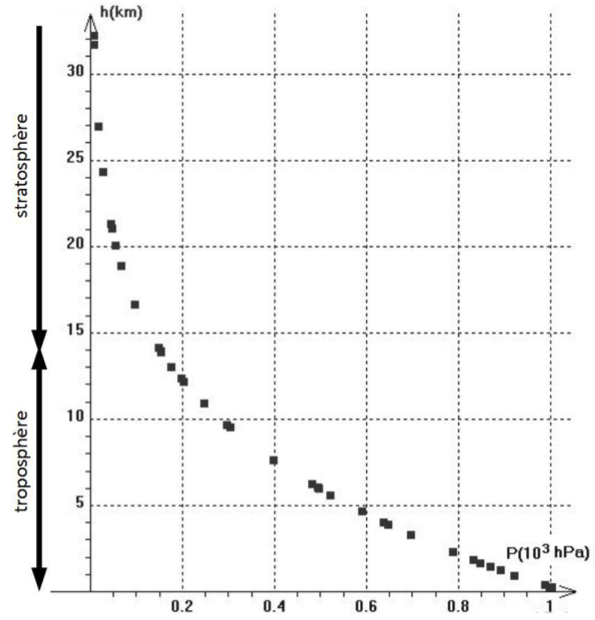
Figure 3 : Relevé de pression dans la troposphère et la stratosphère pour
différentes altitudes h. (D’après : Concours Centrale-Supélec, TSI, 2008.)

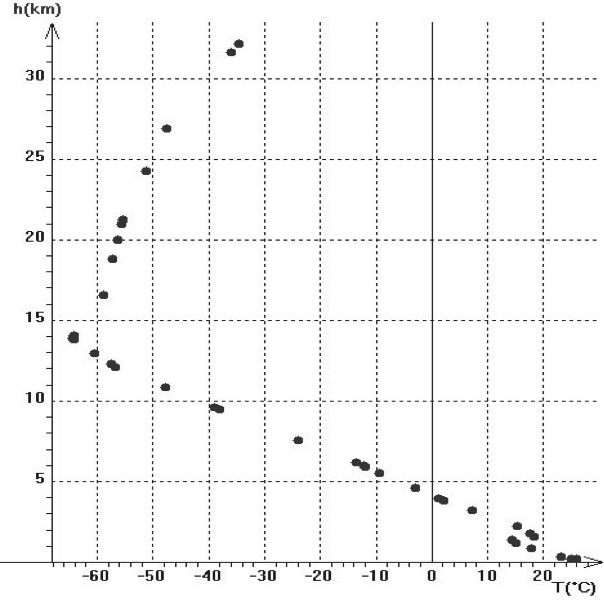
Figure 4 : Relevé de température dans la troposphère et la stratosphère pour différentes altitudes h. (D’après : Concours Centrale-Supélec, TSI, 2008.)

3.1. À l’aide de la figure 3, expliquer comment varie la pression dans le ballon sonde lorsque l’altitude augmente.

D’après la figure 3, lorsque l’altitude augmente, la pression dans le ballon sonde diminue.

3.2. Énoncer la loi de Mariotte relative au produit de la pression P par le volume V d’un gaz pour une quantité de matière donnée et une température constante.

Pour une quantité de gaz constante, à une température constante le produit de la pression p et du volume V est constant : P.V=Constante

3.3. À l’aide de la loi de Mariotte, indiquer comment varie qualitativement le volume du ballon au cours de son ascension. Déterminer ensuite l’altitude maximale atteinte par le ballon au moment de l’éclatement.

$P_{\max }\times V_{\max }=P_{0}\times V_{0}$

$P_{\max }=\frac{P_{0}\times V_{0}}{V_{\max }}$

$P_{\max }=\frac{1,0.10^3\times 4,0}{51}=78\ hPa=0,078.10^3hPa$

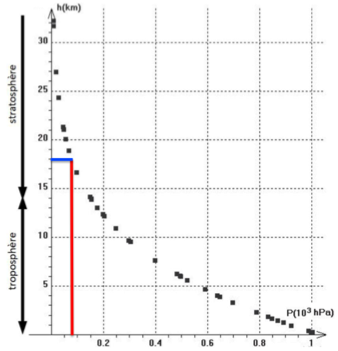
Graphiquement, cette pression correspond à une altitude de 18 km.

3.4. En réalité le ballon a atteint une altitude de 31 km, elle est supérieure à celle prévue dans la question précédente. Proposer une explication.

La loi de Mariotte est valable pour une température constante. Or d’après la figure 4, la température varie en fonction de l’altitude. Ainsi notre hypothèse de départ est erronée. C’est pourquoi l’altitude réelle est différente de celle calculée précédemment.