Capteur d’arrosage capacitif

Bac Nouvelle Calédonie 2023 Sujet 1

Exercice 3 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°23-PYCJ1NC1

Sujet et corrigé

EXERCICE III – CAPTEUR D’ARROSAGE CAPACITIF (6 points)

Figure 1 : Photographie libre de droit d’un capteur d’humidité

Cet exercice ne s’intéresse qu’à l’étude de la mesure par le capteur de l’humidité réalisé à l’aide d’un condensateur. Tous les autres aspects de gestion de l’arrosage sont volontairement ignorés.

Partie A – Étude de la capacité du capteur en fonction de l’humidité

Le capteur d’humidité comprend un condensateur plan pouvant être schématisé de la manière suivante (figure 2) :

Figure 2 : Représentation schématique d’un condensateur plan

La capacité d’un tel condensateur est exprimée par la relation suivante : $C=\frac{\varepsilon_0,\varepsilon_r,S}{\ell}$ .

Les grandeurs physiques apparaissant dans cette équation sont respectivement :

• 𝐶 la capacité du condensateur en farads (F) ;
• 𝜖₀ la permittivité du vide, l’une des constantes fondamentales de la physique ;
• 𝜖_r la permittivité relative du milieu, caractéristique variable d’un environnement à un autre (grandeur sans unité) ;
• 𝑆 la surface des armatures du condensateur plan qui se font face ;
• 𝓁 la distance entre les deux armatures.

Le principe du capteur réside dans le fait que la capacité du condensateur change en fonction de la proportion d’eau présente dans le sol.

A.1. La permittivité de l’air est 𝜖_r,air = 1,0 alors que celle de l’eau est 𝜖_r,eau = 80. En déduire, parmi l’air et l’eau, le milieu pour lequel la capacité du condensateur sera la plus grande.

$$C=\frac{\epsilon_0\epsilon_rS}{l}$$
La capacité du condensateur est proportionnelle à 𝜖r la permittivité relative du milieu.
$$\epsilon_{r,air}=1,0$$
$$\epsilon_{r,eau}=80$$
$$\epsilon_{r,eau}>\epsilon_{r,air}$$
Ainsi :
$$C_{eau}>C_{air}$$
La capacité du condensateur sera la plus grande dans l’eau que dans l’air.

A.2. Justifier alors que, pour une même charge électrique 𝑞 portée par une armature du condensateur, la tension électrique aux bornes de celui-ci est plus faible quand il est plongé dans l’eau que quand il est laissé à l’air libre.

$$q=C\times U_C$$
$$C\times U_C=q$$
$$U_C=\frac{q}{C}$$
la tension électrique aux bornes du condensateur est inversement proportionnelle à sa capacité C.
$$C_{eau}>C_{air}$$
$${U_C}{eau}<{U_C}{air}$$ : la tension électrique aux bornes du condensateur est plus faible quand il est plongé dans l’eau que quand il est laissé à l’air libre.

Partie B – Étude de la charge d’un condensateur

Le capteur est connecté à un microcontrôleur. Dès que le microcontrôleur est mis en route, cela déclenche la charge du condensateur qui compose le capteur alors que ce dernier est encore dans l’air.

Le système est modélisé par le circuit représenté ci-après (figure 3) comportant un condensateur de capacite 𝐶_air en série avec un générateur idéal de tension, ayant pour tension à ses bornes 𝐸, et une résistance de valeur 𝑅.

On considère que le condensateur est initialement déchargé.

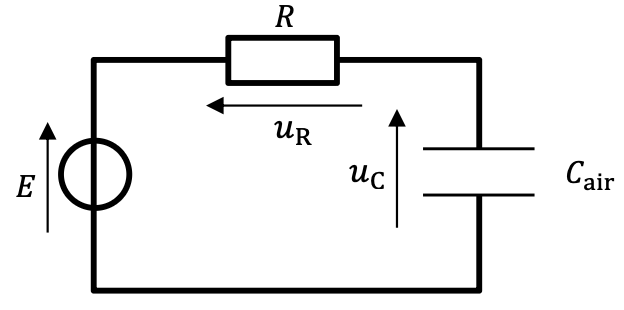
Figure 3 : Circuit en série comprenant un générateur, une résistance 𝑅 et un condensateur 𝐶_air

B.1. Établir, pour le circuit de la figure 3, la relation entre 𝐸, 𝑢_𝑅(𝑡) et 𝑢_𝐶(𝑡).

D’après la loi d’additivité des tensions ou loi des mailles :
$$u_C(t)+u_R(t)=E$$

B.2. Donner la relation mathématique entre l’intensité du courant 𝑖(𝑡) et la charge électrique 𝑞(𝑡) qui traverse une portion de circuit. Préciser les unités de chacune des grandeurs.

$$i(t)=\frac{dq_{(t)}}{dt}$$
Avec :
i(t) : l’intensité du courant en Ampère (A)
q(t) la charge électrique en coulomb (C)

B.3. Montrer alors que l’équation différentielle qui régit l’évolution de la tension 𝑢_𝐶 aux bornes du condensateur est :

$$ \frac{du_C(t)}{dt}+\frac{1}{R \times C_{\text{air}}},u_C(t)=\frac{E}{R \times C_{\text{air}}} $$

$$u_C(t)+u_R(t)=E$$

$$u_C(t)+u_R(t)=E$$

or $$u_R(t)=R\times i$$
$$u_C(t)+R\times i\ =E$$

Or
$$i(t)=\frac{dq_{(t)}}{dt}$$

$$u_C(t)+R\times\frac{dq_{(t)}}{dt}\ =E$$

Or
$$q(t)=C_{air}\times U_C(t)$$

D’ou
$$u_C(t)+R\times\frac{dC_{air}\times u_C(t)}{dt}\ =E$$

$$u_C(t)+R{\times C}{air}\frac{du_C(t)}{dt}=E$$
On divise par $$R{\times C}{air}$$
$$\frac{u_C(t)}{R{\times C}{air}}+\frac{dU_C(t)}{dt}=\frac{E}{R{\times C}{air}}$$
$$\frac{dU_C(t)}{dt}+\frac{u_C(t)}{R{\times C}{air}}=\frac{E}{R{\times C}{air}}$$
$$\frac{dU_C(t)}{dt}+\frac{1}{R{\times C}{air}}u_C(t)=\frac{E}{R{\times C}{air}}$$

B.4.1. Montrer que $ u_C(t)=E \times \left(1-e^{-\frac{t}{\tau}}\right)$ est solution de l’équation différentielle à condition que 𝜏 = 𝑅 × 𝐶_air .

Vérifions que la solution de cette équation différentielle est de la forme :
$$u_C\left(t\right)=E\times\left(1-e^{-\frac{t}{\tau}}\right)$$

-Dérivons $U_C\left(t\right)$ :

$$\frac{du_C(t)}{dt}=E\times -1\times -\frac{1}{\tau}\times e^{-\frac{t}{\tau}}$$
$$\frac{du_C(t)}{dt}=\frac{E}{\tau}\times e^{-\frac{t}{\tau}}$$

-Remplaçons $U_C\left(t\right)$ et $\frac{dU_C(t)}{dt}$ dans l’équation :
$$\frac{du_C(t)}{dt}+\frac{1}{R{\times C}{air}}u_C(t)=\frac{E}{R{\times C}{air}}$$

$$\frac{E}{\tau}e^{-\frac{t}{\tau}}+\frac{E\left(1-e^{-\frac{t}{\tau}}\right)}{R{\times C}{air}}=\frac{E}{R{\times C}{air}}$$
$$\frac{E}{\tau}e^{-\frac{t}{\tau}}+\frac{E}{R{\times C}{air}}-\frac{Ee^{-\frac{t}{\tau}}}{R{\times C}{air}}=\frac{E}{R{\times C}{air}}$$
$$Ee^{-\frac{t}{\tau}}\left(\frac{1}{\tau}-\frac{1}{R{\times C}{air}}\right)=0$$

Un produit de facteur est nul si un des facteurs est nul :
$$\frac{1}{\tau}-\frac{1}{R{\times C}{air}}=0$$
$$\frac{1}{\tau}=\frac{1}{R{\times C}{air}}$$
$$\tau=R{\times C}_{air}$$

Ainsi, $$u_C\left(t\right)=E\times\left(1-e^{-\frac{t}{\tau}}\right)$$ est solution de l’équation différentielle à condition que $$\tau=R{\times C}_{air}$$.

B.4.2. Nommer le produit des grandeurs 𝑅 et 𝐶_air .

Le produit des grandeurs 𝑅 et 𝐶_air est appelé la constante de temps $$\tau$$.

B.5. Montrer qu’une fois avoir attendu un temps suffisamment long, la charge du condensateur vaut 𝑄_chargé = 𝐶_air × 𝐸.

$$u_C\left(t\right)=E\times\left(1-e^{-\frac{t}{\tau}}\right)$$
Une fois avoir attendu un temps suffisamment long $t\rightarrow\infty$
$$u_C\left(t\rightarrow\infty\right)=E\times\left(1-e^{-\frac{\infty}{\tau}}\right)$$
$$u_C\left(t\rightarrow\infty\right)=E\times\left(1-0\right)$$
$$u_C\left(t\rightarrow\infty\right)=E$$

Or
$$U_C=\frac{q}{C}$$

$$U_C(t\rightarrow\infty)=\frac{Q_{chargé}}{C_{air}}$$

Ainsi :
$$\frac{Q_{chargé}}{C_{air}}=E$$
$$Q_{chargé}=E\times C_{air}$$

PARTIE C – Utilisation en situation du capteur

Le moniteur série associé au microcontrôleur permet de récupérer la valeur lue sur le pin A0 (ou broche A0) de connexion du capteur sur le microcontrôleur.

Lorsque le capteur est placé dans l’air, la valeur obtenue, 595, est reportée ligne 5 du script fourni sur la figure 4.

Ensuite, le capteur est plongé uniquement dans l’eau : la valeur obtenue sur le moniteur série est de 217.

Une fois ces deux valeurs déterminées, le capteur est planté dans la terre d’un pot de plante verte : la valeur alors mesurée est comprise entre les valeurs minimale et maximale préalablement trouvées.

1 /*
2 * Script permettant d’obtenir une mesure relative de l’humidité
3 */
4
5 const int sec = 595; // la constante « sec » enregistre la valeur lue lorsque le capteur est dans l’air
6 const int eau = ; // À COMPLÉTER. Définir la constante « eau » qui enregistre la valeur lue lorsque le capteur est dans l’eau
7
8 void setup()
9 {
10 Serial.begin(9600);
11 }
12
13 void loop()
14 {
15 int valeur_exp = analogRead(A0); // Le capteur est branché sur le pin A0.
16
17 int pourcentage_humidite = ; // À COMPLÉTER. Définir une variable entière : le pourcentage d’humidité relative
18
19 Serial.print(« Le pourcentage d’humidité est : « ); // Ces trois lignes affichent sur le moniteur série la valeur de
20 Serial.print(pourcentage_humidite); // l’humidité sous forme d’un pourcentage. Par exemple :
21 Serial.println( » % »); // « Le pourcentage d’humidité est : 40% »
22
23 delay(1000); // Permet d’attendre 1 seconde avant la prochaine mesure
24 }

Figure 4 : Code du microcontrôleur pour la mesure de l’humidité relative du milieu

C.1. Recopier puis compléter la ligne 6 afin d’y faire figurer la valeur mesurée par le capteur dans le cas où il est uniquement dans l’eau.

6 const int eau =217; // À COMPLÉTER. Définir la constante « eau » qui enregistre la valeur
lue lorsque le capteur est dans l’eau

C.2. Expliquer pourquoi la valeur mesurée par le capteur une fois mis dans le pot de la plante sera forcément comprise entre 217 et 595.

Lorsque le capteur est placé dans l’air, la valeur obtenue est 595.
Lorsque le capteur est placé dans l’eau, la valeur obtenue est 217.
La terre ne peut pas être plus sèche que l’air ni plus humide que l’eau. Ainsi la valeur mesurée par le capteur une fois mis dans le pot de la plante sera forcément comprise entre 217 et 595.

C.3. Proposer une expression littérale permettant de déterminer le pourcentage d’humidité relative quand le capteur est en cours d’utilisation dans un pot en fonction des variables « valeur_exp », « sec » et « eau ».

$$Pourcentage\ d’humidité\ relative=\frac{«valeur_exp»-«sec»}{«eau»-«sec»}\times 100$$

C.4. Donner alors le code à écrire à la ligne 17 qui réalise le calcul de la valeur pour la variable « pourcentage_humidite ».

17        int pourcentage_humidite = (valeur_exp- sec)/(eau- sec)*100  ; // À COMPLÉTER. Définir une variable entière : le pourcentage d’humidité relative