Bac Amérique du nord 2025 Sujet 2
Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°25-PYCJ2AN1
Sujet et corrigé
Le combustible utilisé dans les réacteurs nucléaires est de l’uranium enrichi. Après trois ou quatre ans d’utilisation en moyenne, ce combustible est retiré du réacteur. 95% de ce combustible usé est de l’uranium qui peut faire l’objet d’un nouvel enrichissement en vue de la fabrication d’un nouveau combustible. Une autre partie (1%) est du plutonium qui peut être utilisé dans la fabrication d’un autre combustible appelé MOX. Les 4% restant sont les produits de fissions et les actinides mineurs et constituent des déchets ultimes.
Source : d’après l‘ANDRA « 6 questions pour mieux comprendre la gestion des déchets radioactifs à haute activité »
Le combustible MOX est un combustible nucléaire constitué de plutonium 239 et d’uranium appauvri retirés des réacteurs nucléaires après une première utilisation. Cela participe au recyclage des déchets nucléaires. La moitié des réacteurs nucléaires français utilise en partie du combustible MOX. Les futurs réacteurs pourront utiliser 100 % de MOX.
Source : d’après Wikipédia
L’objectif de cet exercice est d’étudier l’intérêt du combustible MOX.
Données :
- L’âge de la Terre est estimé à 4,5 milliards d’années ;
- Masse molaire du plutonium 239 : 239 g·mol-1 ;
- Nombre d’Avogadro : NA = 6,02 × 1023 mol-1 ;
- Temps de demi-vie t1/2 de différents noyaux radioactifs (Tableau 1) :
| Éléments | Uranium | Uranium | Plutonium | Neptunium | Baryum | Plutonium | Krypton |
| Noyaux radioactifs | $^{238}_{92}\mathrm{U}$ | $^{235}_{92}\mathrm{U}$ | $$^{239}{94}\mathrm{Pu}$$ | $^{235}_{93}\mathrm{Np}$ | $^{140}_{56}\mathrm{Ba}$ | $^{235}_{94}\mathrm{Pu}$ | $^{93}_{36}\mathrm{Kr}$ |
| Demi-vie (t1/2) | 4,5×109 ans | 7,04×108 ans | 24 110 ans | 396 jours | 12,8 jours | 25 min | 1,3 s |
Q.1. Donner la composition du noyau d’uranium 235.
Composition du noyau d’uranium 235 ${_{92}^{235}}U$ :
- 92 protons
- 235 − 92 = 143 neutrons
Q.2. Indiquer, en justifiant la réponse, le ou les noyau(x) radioactif(s) isotope(s) de l’uranium 235 parmi ceux présentés dans le tableau 1.
Des noyaux isotopes possèdent le même nombre de protons Z et un nombre de neutrons N différents.
Le noyau radioactif isotope de l’uranium 235 est l’uranium 238 : ${_{92}^{235}}U$.
Q.3. Expliquer pourquoi l’uranium 238 est toujours présent à l’état naturel depuis l’origine de la Terre, contrairement au plutonium 239.
Au bout de 7 demie vie, plus de 99% des atomes radioactifs se sont désintégrés.
$$7\ t_{1/2}=7\times24\ 110=1,68\times{10}^5\ ans$$
Au bout de cent soixante-huit mille ans il reste moins de 1% des atomes initialement présents.
Or la Terre est âgée de 4,5 milliards d’années.
Ainsi, il ne reste plus de plutonium 239 à l’état naturel.
L’uranium 238 à une demie vie de 4,5 milliards années soit l’âge de la Terre. Il reste donc la moitié des noyaux d’uranium 238 initialement présents à l’origine de la Terre.
L’équation de la réaction de la fission du noyau d’uranium 235, percuté par un neutron, en krypton 93, en baryum 140 et en neutrons, noté 1n, s’écrit :
$$^{235}_{92}\mathrm{U} + ^{1}_{0} n \rightarrow\ ^{93}_{36}\mathrm{Kr} +\ ^{140}_{56}\mathrm{Ba} + 3^{1}_{0} n$$
Q.4. Expliquer en quoi ce type de réaction nucléaire peut être qualifié de réaction en chaîne.
$$^{235}_{92}\mathrm{U} + ^{1}_{0} n \rightarrow\ ^{93}_{36}\mathrm{Kr} +\ ^{140}_{56}\mathrm{Ba} + 3^{1}_{0} n$$
Cette réaction de fission a besoin d‘un neutron. Or trois neutrons sont produits. Ils pourront à leur tour causer une réaction de fission.
C’est pourquoi ce type de réaction nucléaire peut être qualifié de réaction en chaîne.
Quant à lui, le plutonium 239 contenu dans le combustible usé est issu des noyaux d’uranium 238 qui, par capture d’un neutron, peuvent se transformer en uranium 239. L’uranium 239 peut ensuite subir deux désintégrations β- successives conduisant au plutonium 239.
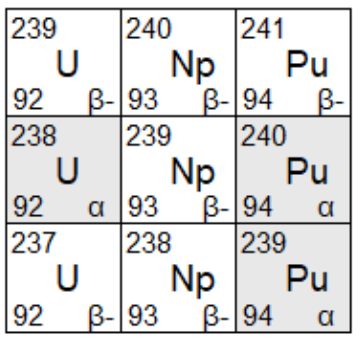
Document 1. Extrait du diagramme N/Z indiquant le type de radioactivité des radionucléides
Q.5. Écrire, à l’aide du diagramme N/Z du document 1, les trois équations des réactions successives permettant de passer de l’uranium 238 au plutonium 239 puis donner le nom de la particule émise lors d’une désintégration β–.
Le plutonium 239 contenu dans le combustible usé provient de l’uranium 238 :
$${_{92}^{238}}U+{_0^1}n\longrightarrow {_{92}^{239}}U$$
Puis désintégrations β− successives :
$${_{92}^{239}}U\longrightarrow {_{93}^{239}}Np+{_{-1}^0}e$$
$${_{94}^{239}}Np\longrightarrow {_{94}^{239}}Pu+{_{-1}^0}e$$
Le plutonium 239 se désintègre suivant l’équation :
$$^{239}_{94}\mathrm{Pu} \rightarrow\ ^{235}_{92}\mathrm{U} +\ ^{4}_{2}\mathrm{He}$$
Q.6. Indiquer à quel type de radioactivité correspond cette désintégration.
$${_{94}^{239}}Pu\longrightarrow {_{92}^{235}}U+{_2^4}He$$
Cette désintégration crée un noyau d’hélium ${_2^4}He$ : c’est une désintégration alpha.
On donne la loi de décroissance radioactive : N(t) = N0·e–λt où N0 est le nombre de noyaux à l’instant t = 0 s et λ est la constante radioactive du noyau radioactif considéré.
Q.7. Établir l’expression de la constante radioactive λ en fonction du temps de demi-vie t1/2. En déduire que la valeur de la constante radioactive du plutonium 239 est 9,1 × 10-13 s-1.
t_{1/2} est la durée au bout de laquelle le nombre de noyau radioactif (ou l’activité) a été divisée par 2.
$$N(t_{1/2})=\frac{N_0}{2}$$
Or
$$N(t_{1/2})=N_0\times e^{-\lambdat_{1/2}}$$
Ainsi
$$N_0\times e^{-\lambda t_{1/2}}=\frac{N_0}{2}$$
$$e^{-\lambda t_{1/2}}=\frac{1}{2}$$
$$ln\left(e^{-\lambda t_{1/2}}\right)=ln\left(\frac{1}{2}\right)$$
$$-\lambda t_{1/2}=-ln\left(2\right)$$
$$\lambda=\frac{ln\ 2}{t_{1/2}}$$
$$\lambda=\frac{ln\ 2}{24\ 110\times 365,25\times 24\times 60\times 60}$$
$$\lambda=9,1\times {10}^{-13}\ s^{-1}$$
Données :
- L’activité A d’un échantillon radioactif est le nombre de désintégrations par seconde (en becquerel (Bq), avec 1 Bq = 1 s-1) et elle est liée au nombre N de noyaux radioactifs présents dans l’échantillon par la relation : A(t) = λ·N(t).
- Classification des déchets radioactifs (Tableau 2) :
| TEMPS DE DEMI-VIE | ||||
| Vie très courte (demi-vie < 100 jours) | Vie courte (demi-vie ≤ 31 ans) | Vie longue (demi-vie > 31 ans) | ||
| ACTIVITE MASSIQUE * | Très faible activité TFA (< 100 Bq·g-1) | Gestion par décroissance radioactive sur le site de production puis évacuation dans les filières conventionnelles | Stockage de surface (au Centre Industriel de Regroupement, d’Entreposage et de Stockage – CIRES) | |
| Faible activité FA (< 105 Bq·g-1) | Stockage de surface (au centre de stockage de l’Aube) | Stockage de faible profondeur (à l’étude) | ||
| Moyenne activité MA (< 106 Bq·g-1) | ||||
| Haute activité HA (> 106 Bq·g-1) | Pas encore de filière opérationnelle (stockage réversible profond à l’étude) | |||
* L’activité massique est l’activité rapporté à 1 g d’échantillon D’après andra.fr
Q.8. Montrer, à l’aide du tableau 2, l’intérêt du MOX, en analysant comment sont gérés à l’heure actuelle les déchets de la catégorie à laquelle appartient le plutonium 239.
Le candidat est invité à prendre des initiatives et à présenter sa démarche. Toute démarche pertinente, même non aboutie, sera valorisée.
Calculons l’activité massique du MOX (l’activité massique est l’activité rapporté à 1 g d’échantillon) :
$$A=\lambda\times N$$
Or
$$n=\frac{N}{N_a}$$
$$\frac{N}{N_a}=n$$
$$N=n\times N_a$$
D’où
$$A=\lambda\times n\times N_a$$
Or
$$n=\frac{m}{M}$$
D’où
$$A=\lambda\times \frac{m}{M}\times N_a$$
$$A=9,1\times {10}^{-13}\times \frac{1}{239}\times 6,02\times {10}^{23}$$
$$A=2,3\times {10}^9\ Bq{.g}^{-1}$$
A > 106 Bq·g-1 : c’est une Haute activité massique à vie longue (demi-vie 24 110 > 31 ans), il n’y a pas encore de filière opérationnelle (stockage réversible profond à l’étude) d’où l’intérêt de réutiliser le plutonium 239 pour faire du MOX.
