Comprendre les nuages

Bac Liban 2023 Sujet 2

Exercice 1 – (11 points) –  Durée 1h56 – Calculatrice autorisée

Sujet n°23-PYCJ2LI1

EXERCICE 1 : COMPRENDRE LES NUAGES (11 POINTS)

La physique des nuages est l’étude des processus de formation et d’évolution des nuages et des précipitations qui les accompagnent. Les nuages sont formés de microscopiques gouttelettes. La formation et la stabilité d’un nuage dépendent notamment des mouvements verticaux de l’air dans celui-ci.

Dans une première partie, on étudie l’un des phénomènes permettant au nuage de ne pas tomber. Dans la deuxième et la troisième partie, on s’intéresse à un satellite permettant d’étudier les nuages. Dans la quatrième partie, on interroge le bien-fondé d’une expérience visant à influer sur la météo.

A. Nuage et précipitations

Pourquoi les nuages ne tombent-ils pas ?

Les nuages sont constitués de gouttelettes d’eau de très petit diamètre (de 10 à 100 µm) qui demeurent en suspension dans l’air.

Pour répondre à l’éternelle question « pourquoi les nuages ne tombent-ils pas ? », il faut en premier lieu savoir que la formation des nuages implique le plus souvent des mouvements ascendants d’air, c’est-à-dire des mouvements de l’air vers le haut. En raison de leur faible masse, les gouttelettes entrant dans la constitution du nuage n’ont pas besoin de forces de grande intensité pour être maintenues en équilibre ou être entraînées dans un mouvement ascendant. […]

Finalement, l’état d’équilibre ou de mouvement vertical (ascendance ou chute, sous forme de pluie éventuellement) se ramène à l’étude du bilan entre deux forces colinéaires opposées : le poids de la gouttelette et la résultante verticale des forces d’agitation de l’air.

D’après Météorologie, 100 expériences pour comprendre la météo de Y. Corboz.

Pour mieux comprendre ce qui permet au nuage de rester en suspension, on s’intéresse à une gouttelette d’eau présente dans ce nuage. On modélise la situation de la gouttelette de la façon suivante :

• la gouttelette est supposée sphérique de rayon r = 10 µm ;
• volume d’une sphère :

$$V=\frac{4}{3}\cdot\pi\cdot r^3$$

• la gouttelette n’est soumise qu’à son poids $\overrightarrow{P}$ et à une force verticale $\overrightarrow{F}$  exercée par l’air, dirigée vers le haut ;
• la gouttelette est supposée initialement immobile dans le référentiel terrestre supposé galiléen ;

• la valeur de la force exercée par l’air sur la gouttelette s’exprime de la façon suivante :

F = k · η · r · v

k : coefficient sans unité ; k = 18,8

η : viscosité de l’air ; η = 15×10^-6 kg·m^-1·s^-1

r : rayon de la goutte (en m)

v : vitesse de l’air dans un référentiel lié à la gouttelette (en m·s^-1)

Données :

• intensité du champ de pesanteur : g = 9,8 N·kg^-1 ;
• masse volumique de l’eau à 20 °C : ρ_eau = 1000 kg·m^-3_.

Q.1. Montrer que la valeur P du poids de la goutte est environ 4,1×10^-11 N.

$$
P=m\times g
$$
Or
$$
\rho_{eau}=\frac{m}{V}
$$
$$
m=\rho_{eau}\times V
$$
D’ou
$$
P=\rho_{eau}\times V\times g
$$

Or
$$
V=\frac{4}{3}\times \pi\times r^3
$$
D’ou
$$
P=\rho_{eau}\times\frac{4}{3}\times \pi\times r^3\times g
$$
$$
P=1000\times\frac{4}{3}\times \pi\times\left(10\times{10}^{-6}\right)^3\times9,8
$$
$$
P=4,1\times{10}^{-11}N
$$

Q.2. Déterminer la valeur F de la force verticale ascendante exercée par l’air sur la gouttelette pour une vitesse verticale de l’air de 0,10 m·s^-1.

$$
F=k\times\eta\times r\times v
$$
$$
F=18,8\times15\times{10}^{-6}\times10\times{10}^{-6}\times0,10
$$
$$
F=2,8\times{10}^{-10}\ N
$$

Q.3. En déduire si la goutte monte, tombe ou reste immobile. Justifier.

La force verticale descendante à pour valeur $P=4,1\times{10}^{-11}N$
La force verticale ascendante à pour valeur $F=2,8\times{10}^{-10}\ N=28\times{10}^{-11}\ N$
La force verticale ascendante est supérieure à la force verticale descendante : la goutte monte.

Différents phénomènes (notamment des collisions) peuvent amener le rayon des gouttelettes à augmenter, provoquant leur chute, sous forme de pluie.

On suppose que la vitesse verticale ascendante de l’air reste inchangée.

Q.4. En exploitant les réponses aux questions précédentes, déterminer le rayon minimum que doit posséder une gouttelette pour tomber.

Toute démarche cohérente, même incomplète, sera valorisée.

Pour tomber, il faut que la force verticale descendante $P$ soit supérieure à la force verticale ascendante $F$ :
$$
P>F
$$
$$
\rho_{eau}\times\frac{4}{3}\times \pi\times r^3\times g>k\times\eta\times r\times v
$$
$$
\rho_{eau}\times\frac{4}{3}\times \pi\times r^2\times g>k\times\eta\times v
$$
$$
r^2>\frac{k\times\eta\times v}{\rho_{eau}\times\frac{4}{3}\times \pi\times g}
$$
$$
r>\sqrt{\frac{k\times\eta\times v}{\rho_{eau}\times\frac{4}{3}\times \pi\times g}}
$$

$$
r>\sqrt{\frac{18,8\times15\times{10}^{-6}\times0,10}{1000\times\frac{4}{3}\times \pi\times9,8}}
$$
$$
r>2,6\times{10}^{-5}\ m
$$
$$
r>26\times{10}^{-6}\ m
$$
$$
r>26\ \mu m
$$

Pour tomber, une gouttelette doit posséder un rayon minimum de 26 μm.

B. Earthcare, un satellite pour étudier les nuages

EarthCARE (Earth Clouds, Aerosols and Radiation Explorer) est un satellite d’observation de l’atmosphère terrestre faisant partie du programme Living Planet de l’ESA (European Space Agency). L’un des objectifs de cette mission est d’améliorer notre compréhension du bilan radiatif de la Terre et de ses effets sur le climat. Son lancement est prévu pour 2023. Le satellite effectuera environ 16 fois le tour de la Terre chaque jour.

D’après Wikipédia.

Données :

• constante de gravitation universelle : G = 6,67×10^-11 N·m²·kg^-2 ;
• masse de la Terre : M_T = 5,97×10²⁴ kg ;
• rayon de la Terre : R_T = 6,37×10³ km ;
• on considère que le satellite EarthCARE (noté S, de masse M_S) supposé ponctuel est en mouvement circulaire autour de la Terre à une altitude h = 390 km.

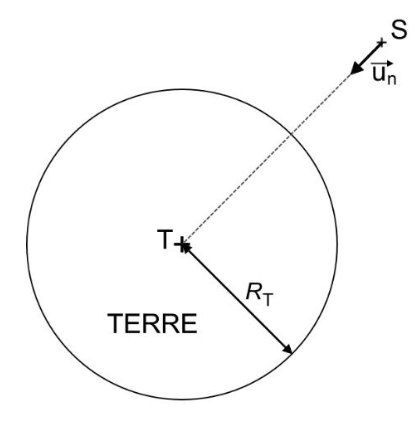
Q.5. Exprimer la force d’interaction gravitationnelle $\overrightarrow{F_{T/S}}$ que la Terre exerce sur le satellite, en fonction notamment du vecteur unitaire $\overrightarrow{u_{n}}$ , de la masse de la Terre M_T, de la masse du satellite M_S, du rayon de la Terre R_T et de l’altitude h.

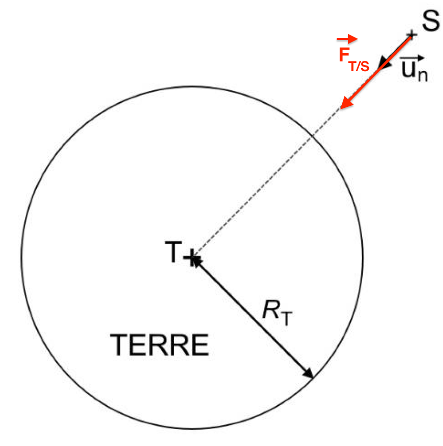
Q.6. En appliquant la seconde loi de Newton et en utilisant le repère de Frenet, montrer que le mouvement du satellite est uniforme.

Système : satellite
Référentiel : géocentrique supposé galiléen.

D’après la 2nd loi de Newton :

$$
\Sigma\overrightarrow {F_{ext}}=M_s\overrightarrow {a}
$$

$$
\overrightarrow {F_{T/S}}=M_s\overrightarrow {a}
$$

$$
G\ \times\frac{M_S\times M_T}{\left(R_T+h\right)^2}{\overrightarrow {u}}_N=M_s\overrightarrow {a}
$$

$$
\overrightarrow {a}=G\ \times\frac{M_T}{\left(R_T+h\right)^2}{\overrightarrow {u}}_N
$$

Pour un mouvement circulaire, dans le repère de Frenet, le overrightarrow teur accélération est de la forme :
$$
\overrightarrow {a}=\frac{v^2}{R_T+h}{\overrightarrow {u}}_N+\frac{dv}{dt}{\overrightarrow {u}}_T
$$

L’accélération étant unique, par identification :
$$
\frac{dv}{dt}=0
$$
donc la vitesse est constante : le mouvement est uniforme

Q.7. Montrer que la valeur de la vitesse v du satellite est donnée par la relation :

$$v=\sqrt{\frac{G \times M_T}{R_T+h}}$$

$$
\overrightarrow {a}=G\ \times\frac{M_T}{\left(R_T+h\right)^2}{\overrightarrow {u}}_N
$$
Pour un mouvement circulaire, dans le repère de Frenet, le overrightarrow teur accélération est de la forme:
$$
\overrightarrow {a}=\frac{v^2}{R_T+h}{\overrightarrow {u}}_N+\frac{dv}{dt}{\overrightarrow {u}}_T
$$

L’accélération étant unique, par identification :
$$
\frac{v^2}{R_T+h}=G\ \times\frac{M_T}{\left(R_T+h\right)^2}
$$
$$
v^2=G\ \times\frac{M_T}{R_T+h}
$$
$$
v=\sqrt{G\ \times\frac{M_T}{R_T+h}}
$$
$$
v=\sqrt{\frac{G\ \times M_T}{R_T+h}}
$$

Q.8. Déduire des questions précédentes que la période de révolution du satellite est donnée par la relation :

$$T=2\pi\sqrt{\frac{\left(R_T+h\right)^3}{G\times M_T}}$$

La période de révolution est :
$$
T=\frac{\text{Périmètre d’un cercle}}{\text{vitesse}}=2\pi Rv=2\pi\frac{R_T+h}{\sqrt{G\ \times\frac{M_T}{R_T+h}}}
$$
$$
T=2\pi\sqrt{\left(R_T+h\right)^2\frac{\left(R_T+h\right)}{G\ \times M_T}}
$$
$$
T=2\pi\sqrt{\frac{\left(R_T+h\right)^3}{G\ \times M_T}}
$$

Q.9. Calculer la valeur de la période de révolution T et déterminer si cette valeur est en accord avec la phrase d’introduction : « Le satellite effectuera environ 16 fois le tour de la Terre chaque jour. »

$$
T=2\pi\sqrt{\frac{\left(R_T+h\right)^3}{G\ \times M_T}}
$$
$$
T=2\pi\sqrt{\frac{\left(6,37\times{10}^3\times{10}^3+390\times{10}^3\right)^3}{6,67\times{10}^{-11}\times5,97\times{10}^{24}}}
$$
$$
T=5,53\times{10}^3\ s
$$

Le satellite effectue un tour en $5,53\times{10}^3\ s$.

1 tour	$5,53\times{10}^3\ s$
N tours	$1\ jour=24\times60\times60\ s$

$$
N=\frac{24\times60\times60\times1}{5,53\times{10}^3}
$$
$$
N=15,6\ tours\approx16\ tours
$$
La valeur la période de révolution $T$ est en accord avec  la phrase d’introduction : « Le satellite effectuera environ 16 fois le tour de la Terre chaque jour. »

C. Radar profileur de nuage

Le satellite Earthcare, en passant au-dessus d’un nuage, pourra faire des analyses de ce nuage grâce à des instruments embarqués. L’un de ces instruments est un radar profileur de nuage, nommé Cloud Profiling Radar (CPR) dont le rôle est notamment d’étudier les mouvements verticaux des gouttelettes dans le nuage.

Le radar CPR envoie vers le nuage des ondes électromagnétiques. Les gouttelettes (dont le diamètre est de l’ordre de 10 à 100 µm) présentes dans le nuage renvoient une partie de ces ondes vers le satellite. Le signal reçu par le satellite est analysé.

Pour obtenir un signal exploitable, la longueur d’onde des ondes électromagnétiques émises par le CPR doit être supérieure à dix fois celle du diamètre des gouttelettes.

D’après Wikipédia.

Données : la longueur d’onde λ (en m), la fréquence f (en Hz) et la célérité d’une onde c (en m·s^-1) sont liées par la relation :

$$\lambda=\frac{c}{f}$$

Le CPR utilise des ondes électromagnétiques de fréquence f_e = 94,05 × 10⁹ Hz.

Q.10. Déterminer si les ondes électromagnétiques utilisées par le CPR permettent d’obtenir un signal exploitable. Justifier la réponse.

Pour obtenir un signal exploitable, la longueur d’onde des ondes électromagnétiques émises par le
CPR doit être supérieure à dix fois celle du diamètre des gouttelettes.

Calculons la longueur d’onde des ondes électromagnétiques émises par le CPR :
$$
\lambda=\frac{c}{f_e}
$$
$$
\lambda=\frac{3,00\times{10}^8}{94,05\times{10}^9}
$$
$$
\lambda=3,2\times{10}^{-3}\ m
$$

Les gouttelettes ont un diamètre qui est de l’ordre de 10 à 100 μm.
Dix fois le diamètre des gouttelettes :
$$
10\ d=10\times100\ \mu m=10\times100\times{10}^{-6}=1,0\times{10}^{-3}m
$$

$\lambda>10\ d$ : le signal est donc exploitable.

Le satellite EarthCARE est situé à 390 km d’altitude à la verticale d’un nuage. Il se déplace à la vitesse v = 7,5×10³ m·s^-1 par rapport au sol. Le nuage de dimension horizontale d’environ 1 km est immobile par rapport au sol et situé à une altitude moyenne de 2 km.

Q.11. Vérifier que la distance parcourue par le satellite durant le temps d’un aller-retour des ondes électromagnétiques entre le satellite et le nuage est très inférieure à la longueur du nuage. On négligera l’épaisseur du nuage.

Le satellite EarthCARE est situé à 390 km d’altitude à la verticale d’un nuage. Le nuage est situé à une altitude moyenne de 2 km.

Distance entre le satellite et le nuage :
$$
390-2=388\ km
$$

Distance aller-retour entre le satellite et le nuage :
$$
2\times388\ km=776\ km
$$

Calculons le temps d’un aller-retour des ondes électromagnétiques entre le satellite et le nuage :
$$
c=d_{aller-retour}\Delta t
$$
$$
\Delta t=\frac{d_{aller-retour}}{c}
$$
$$
\Delta t=\frac{776\times{10}^3}{3,00\times{10}^8}
$$
$$
\Delta t=2,58\times{10}^{-3}\ s
$$

Calculons la distance parcourue par le satellite durant le temps d’un aller-retour des ondes électromagnétiques entre le satellite et le nuage :
$$
v=\frac{d}{\Delta t}
$$
$$
d=v\times\Delta t
$$
$$
d=7,5\times{10}^3\times2,58\times{10}^{-3}
$$
$$
d=19\ m
$$

$$
d\ll2\ km
$$

La distance parcourue par le satellite durant le temps d’un aller-retour des ondes électromagnétiques entre le satellite et le nuage est de 19m. Elle est très inférieure à la longueur du nuage.

D. Une expérience contestée

En février 2021, divers journaux ont rapporté une expérience scientifique étonnante. Une équipe de l’université chinoise de Qinghai vient de tester l’effet d’un son très puissant : sous l’influence des ondes acoustiques émises à 160 dB, les précipitations auraient augmenté.

La mesure du niveau sonore de 160 dB a été réalisée à 1,0 m du haut-parleur.

Dans un article en ligne du journal anglais Dailymail du 5 février 2021, un journaliste relate avec enthousiasme cette expérience et affirme que les ondes sonores utilisées sont à peine audibles.

Données :

–     le niveau d’intensité sonore L (en dB) est défini par :

$$L=10\log\left(\frac{I}{I_0}\right)$$

I et I₀ sont exprimés en W·m^-2 ; I₀ = 1,0×10^-12 W·m^-2 ;

• l’intensité sonore I (en W·m^-2) est liée à la puissance sonore P (en W) rayonnée par la source, qui se répartit au cours de la propagation sur une surface d’aire S (en m²) :

$$I=\frac{P}{S}$$

avec S = 4 π · d ² où d (en m) est la distance qui sépare le récepteur de la source ;

• échelle de niveau d’intensité sonore (en dB) :

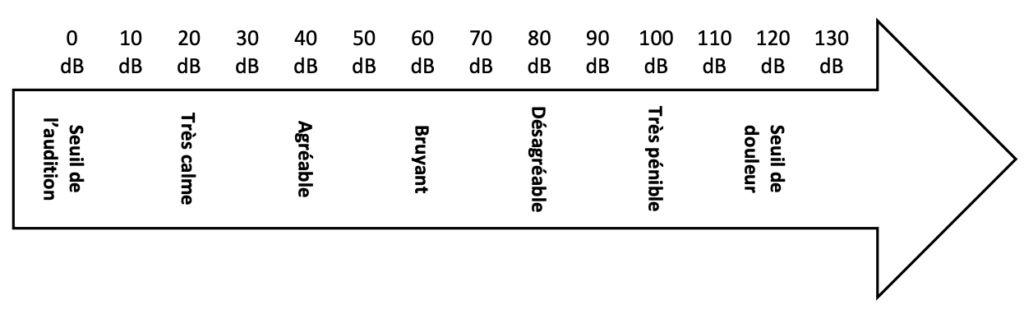
Pendant l’expérience réalisée par l’université chinoise de Qinghai, une personne se place à une distance d du haut-parleur.

Q.12. Estimer la distance d minimale pour qu’une personne ne subisse pas de gêne liée au bruit du haut-parleur. Commenter le point de vue du journaliste.

Les hypothèses formulées par le candidat pour modéliser la situation devront être explicitées. La démarche suivie devra être clairement exposée et les calculs devront être détaillés.

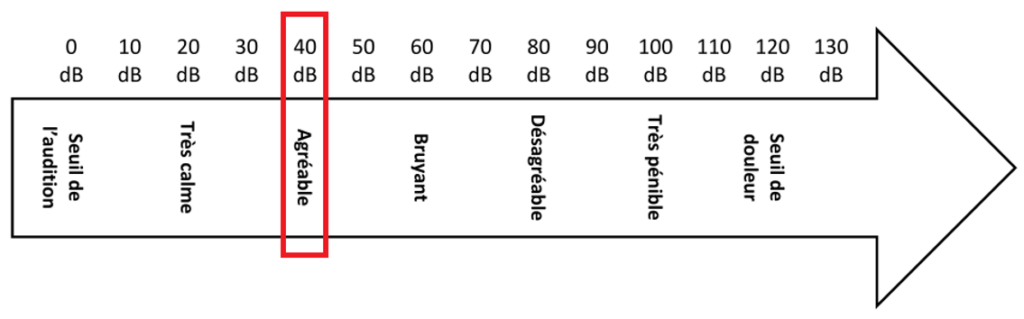
Pour une personne ne subisse pas de gêne liée au bruit du haut-parleur, le bruit doit être agréable soit 40 dB.
$$
I=\frac{P}{S}
$$
Or
$$
S=4\pi d^2
$$
$$
I=\frac{P}{4\pi d^2}
$$

D’ou
$$
P=I\times4\pi d^2
$$

La puissance est la même pour $d_1$ et $d_2$ :
$$
I_2\times4\pi d_2^2=I_1\times4\pi d_1^2
$$

$$
d_2^2=\frac{I_1\times d_1^2}{I_2}
$$
$$
d_2=\sqrt{\frac{I_1\times d_1^2}{I_2}}
$$
$$
d_2=\sqrt{\frac{I_1}{I_2}}\times d_1
$$

Or
$$
L=10\log\left(\frac{I}{I_0}\right)
$$
$$
10\log\left(\frac{I}{I_0}\right)=L
$$
$$
\log\left(\frac{I}{I_0}\right)=\frac{L}{10}
$$
$$
\frac{I}{I_0}={10}^\frac{L}{10}
$$
$$
I=I_0\times{10}^\frac{L}{10}
$$
$$
I_1=I_0\times{10}^\frac{L_1}{10}
$$
$$
I_2=I_0\times{10}^\frac{L_2}{10}
$$

D’ou
$$
d_2=\sqrt{\frac{I_1}{I_2}}\times d_1
$$
$$
d_2=\sqrt{\frac{I_0\times{10}^\frac{L_1}{10}}{I_0\times{10}^\frac{L_2}{10}}}\times d_1
$$
$$
d_2=\sqrt{\frac{{10}^\frac{L_1}{10}}{{10}^\frac{L_2}{10}}}\times d_1
$$
$$
d_2=\sqrt{\frac{{10}^\frac{160}{10}}{{10}^\frac{40}{10}}}\times1,0
$$
$$
d_2=1,0\times{10}^6\ m
$$
$$
d_2=1,0\times{10}^3\ km
$$
$$
d_2=1000\ km
$$

Le journaliste pouvait entendre le son jusqu’à 1000 km. Quand il affirme que les ondes sonores utilisées sont à peine audibles il devait soit se trouver dans un autre pays soit il souffre de surdité pour en pas l’avoir entendu.