De l’or pour lutter contre les bactéries

Sujet avec enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h12 – 12 points – Thème « Une longue histoire de la matière »

Les antibiotiques sont des substances chimiques capables de tuer les bactéries ou d’empêcher leur reproduction.

La surutilisation des antibiotiques depuis la maîtrise de leur extraction et de leur synthèse a conduit à l’apparition de souches bactériennes résistantes aux antibiotiques connus. La lutte contre la résistance aux antibiotiques est devenue un enjeu majeur de santé publique ces dernières années. Dans ce contexte, les nano- antibiotiques, composés de nanoparticules d’or à la surface desquelles sont greffés des antibiotiques, présentent souvent des propriétés exceptionnelles, allant même jusqu’à contourner les mécanismes de résistance bactérienne.

Illustration d’un nano-antibiotique

Source : d’après https://theses.hal.science

Dans cet exercice, on cherche à étudier la structure des nanoparticules d’or et leur utilisation dans la lutte contre les bactéries.

On rappelle que l’or est l’élément chimique de symbole Au. C’est un métal précieux de couleur jaune et présentant un fort éclat.

Document 1 : Un nano-objet constitué d’or

Image au microscope électronique du nano-objet

Modèle atomique simplifié du nano- objet (chaque sphère correspond à un atomed’or)

Source : d’après https://rtflash.fr

Une nanoparticule est un nano-objet dont la dimension caractéristique est inférieure à 100 nm.

Source : d’après https://biologiedelapeau.fr

Graphique 1 donnant le nombre d’atomes d’or Nor dans une nanoparticule en fonction de son rayon r en nm : N_or= f (r)

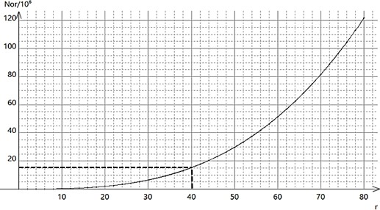
Source : d’après synthese-de-nanoparticule-dor-et-leur-caracterisation-par-granulometrie-

laser.pdf (univ-tlemcen.dz)

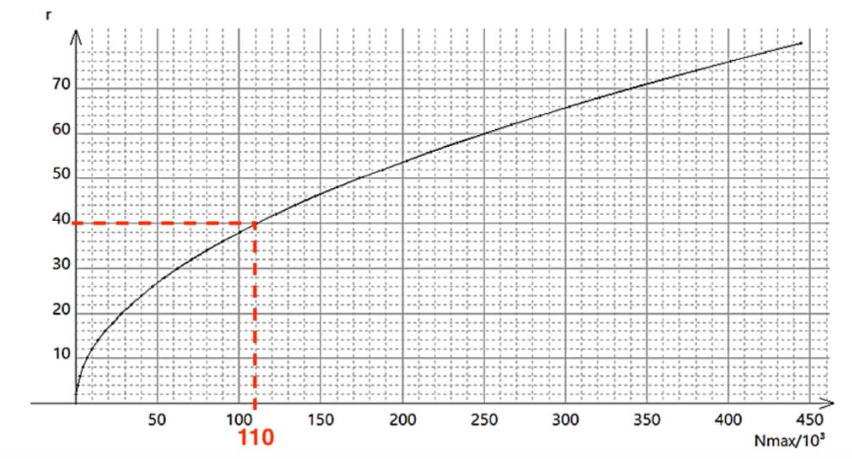
Graphique 2 donnant le rayon r de la nanoparticule en nm en fonction du nombre maximum Nmax d’atomes d’or utiles en surface : r = f (Nmax)

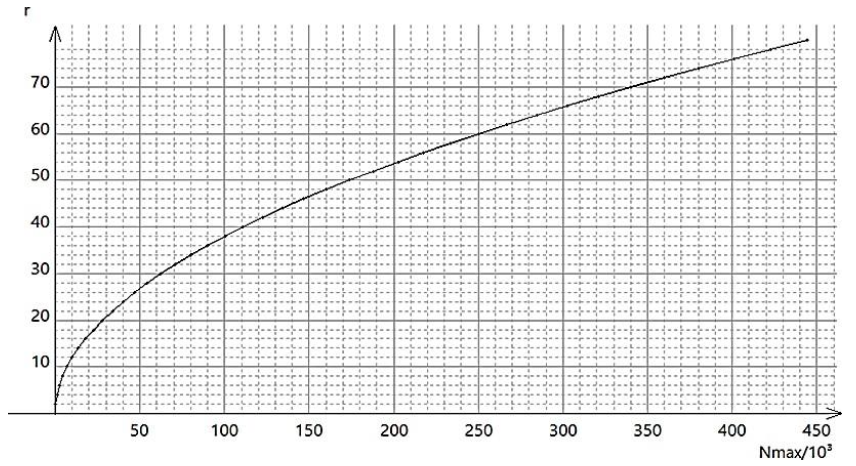
Un atome utile en surface est un atome sur lequel on peut greffer un antibiotique.

Source : d’après synthese-de-nanoparticule-dor-et-leur-caracterisation-par-granulometrie-laser.pdf (univ-tlemcen.dz)

Document 2 : Organisation microscopique d’une nanoparticule d’or

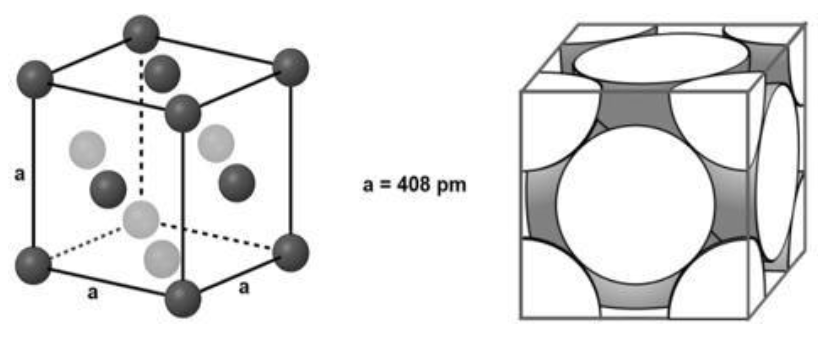
À l’état microscopique, les nanoparticules d’or sont organisées selon un réseau dont les mailles élémentaires sont dites « cubiques faces centrées ». Une maille élémentaire de ce type est représentée ci-dessous de deux manières en perspective cavalière.

Outil pour dénombrer les entités dans une maille :

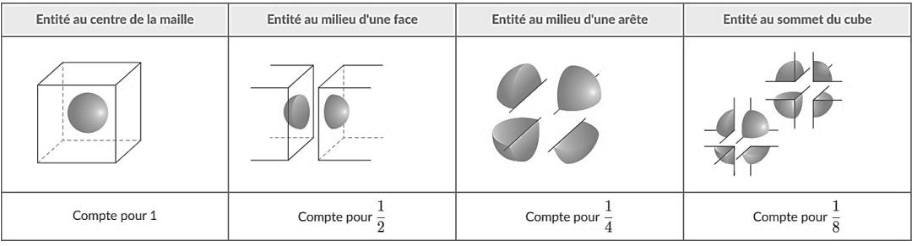
Source : d’après https://www.lelivrescolaire.fr/page/5737687

Données :

Masse d’un atome d’or : 3,27×10^-25 kg
1 g = 10^-3 kg
1 cm = 10^-2 m
1 nm = 10^-9 m
1 pm = 10^-12 m
Volume d’un cube d’arête a : V = a³

Document 3 : Action de nanoparticules Ampicilline-Or sur quelques souches bactériennes

L’ampicilline est un antibiotique qui peut être greffé sur des nanoparticules d’or.

*Efficacité de l’ampicilline sur différentes souches bactériennes*
Souche bactérienne	CMI Ampicilline (μg·mL^-1)	CMI Ampicilline greffée sur nanoparticule d’or (μg·mL^-1)
Escherichia coli (souche 1)	125	15,6
Escherichia coli (souche 2)	250	62,5
Staphylococcus aureus	125	7,8
Bacillus subtilis	31	7,8
Flavobacterium devorans	250	125

1 – Vérifier que le nano-objet photographié au document 1, sur lequel les atomes sont clairement visibles, est bien une nanoparticule et que celle-ci relève de l’état cristallin.

D’après le document 1 : « Une nanoparticule est un nano-objet dont la dimension caractéristique est inférieure à 100 nm. »

A l’aide de la photographie, calculons son rayon :

Schéma	Réel
1 cm	2 nm
4,1 cm	r

$r=\frac{4,1\times2}{1}$

r=8,2 nm

r<100 nm : c’est bien une nanoparticule.

De plus, les atomes sont assemblés de manière régulière : c’est caractéristique de l’état cristallin.

Ainsi, ce nano-objet photographié au document 1 est bien une nanoparticule et que celle-ci relève de l’état cristallin.

2 – Justifier l’appellation « cubique faces centrées » de la maille élémentaire représentée au document 2.

Un cristal est dit cubique à faces centrées lorsque les nœuds de son réseau sont situés :

aux huit sommets d’un cube ;
au centre de chacune des faces de ce cube.

La maille élémentaire représentée au document 2 contient bien un atome sur chaque sommet du cube et un atome sur chaque face : c’est un cristal cubique faces centrées.

3 – Montrer que cette maille élémentaire contient 4 atomes d’or et calculer leur masse totale.

Il y a 8 atomes sur les sommets qui sont dans 1/8 de la maille.

Il y a 6 atomes sur les faces qui sont dans 1/2 de la maille.

$N=8\times\frac{1}{8}+6\times\frac{1}{2}=4$

Il y a 4 atomes d’or dans une maille.

La masse d’un atome d’or est de 3,27×10^-25 kg

Pour une maille :

$m_{maille}=4\timesm_{atome}$

$m_{maille}=4\times3,27\times{10}^{-25}$

$m_{maille}=1,31\times{10}^{-24}\ Kg$

4 – Calculer le volume de cette maille élémentaire.

$V_{maille}=a^3$

$V_{maille}=\left(408 \times {10}^{-12}\right)^3$

$V_{maille}=6,79 \times {10}^{-29}\ m^3$

5 – Déduire des questions 3- et 4- que la masse volumique d’une maille élémentaire de nanoparticule d’or est égale à celle de l’or métallique à savoir 19,3 g·cm^-3.

$\rho=\frac{m_{maille}}{V_{maille}}$

$\rho=\frac{1,31 \times {10}^{-24}}{6,79 \times {10}^{-29}}$

$\rho=19\ 293\ Kg.m^{-3}$

Calcul pour avoir la masse volumique en g·cm^-3 :

$\rho=\frac{m_{maille}}{V_{maille}}$

$\rho=\frac{1,31 \times {10}^{-24} \times {10}^3}{6,79 \times {10}^{-29}\times{10}^6}$

$\rho=19,\ 3\ g.{\rm cm}^{-3}$

Ainsi, la masse volumique d’une maille élémentaire de nanoparticule d’or est égale à celle de l’or métallique à savoir 19,3 g·cm^-3.

6 – Une nanoparticule d’or, sur laquelle des antibiotiques peuvent être greffés, a un rayon moyen de 40 nm. Le graphique 1 du document 1 nous indique qu’une telle nanoparticule est constituée de 15×10⁶ atomes d’or. À l’aide du graphique 2, préciser dans ce cas le nombre d’atomes d’or utiles en surface.

Pour un rayon moyen de 40 nm, le graphique 2 du document 1 nous indique qu’une telle nanoparticule est constituée de 110×10³ atomes d’or utiles en surface.

7- Calculer le pourcentage d’atomes d’or utiles en surface d’une nanoparticule de 40 nm de diamètre.

$P=\frac{N_{atomes\ dor\ utiles\ en\ surface}}{N_{atomes\ dor}}$

$P=\frac{110 \times {10}^3}{15 \times {10}^6}$

P=0,0069

P=0,69 %

8 – Louis Pasteur, pionnier de la microbiologie, a affirmé : « Dans la nature, le rôle de l’infiniment petit est infiniment grand ». Commenter cette affirmation en analysant le cas des nanoparticules d’or greffées d’ampicilline, illustré par les documents de l’exercice.

Le document 3 nous montre qu’avec une nanoparticule d’or, la plus petite concentration en antibiotique nécessaire pour bloquer la croissance d’une souche bactérienne diminue.

Ainsi, en utilisant une particule infiniment petite, elle produit des effets infiniment grands.