Des écoulements sanguins

Nouvelle Calédonie 2025 Sujet 1

Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ1NC1

EXERCICE 2 – DES ÉCOULEMENTS SANGUINS (5 points)

Le but de cet exercice est d’étudier deux situations d’écoulement du sang dans le système veineux constitué d’artères, de veines et de capillaires.

La sténose aortique est une pathologie cardiaque consistant en un rétrécissement du diamètre de la valve aortique. Celle-ci se trouve entre le ventricule gauche du cœur et le principal vaisseau du corps humain, l’aorte.

Par ailleurs, la communication entre artère et veine se fait par un réseau de plusieurs millions de capillaires.

Partie A – Mise en évidence d’une sténose aortique Données :

Relation de Bernoulli : elle est valable pour un fluide parfait (sans viscosité) et incompressible, en écoulement permanent (indépendant du temps). On considère que le fluide n’est soumis qu’aux forces de pression et de pesanteur.

D’après cette relation, pour deux points A et B situés le long d’une même ligne de courant (voir figure 1) :

$$P_A+\rho \times g \times z_A+\frac{1}{2}\times \rho \times v_A^2=P_B+\rho \times g \times z_B+\frac{1}{2}\times \rho \times v_B^2$$

P désigne la pression en un point et s’exprime en pascals (Pa), r est la masse volumique du fluide en kg·m–3, g est l’intensité de la pesanteur en N·kg^–1 et z représente l’altitude du point considéré et s’exprime en mètres (m).

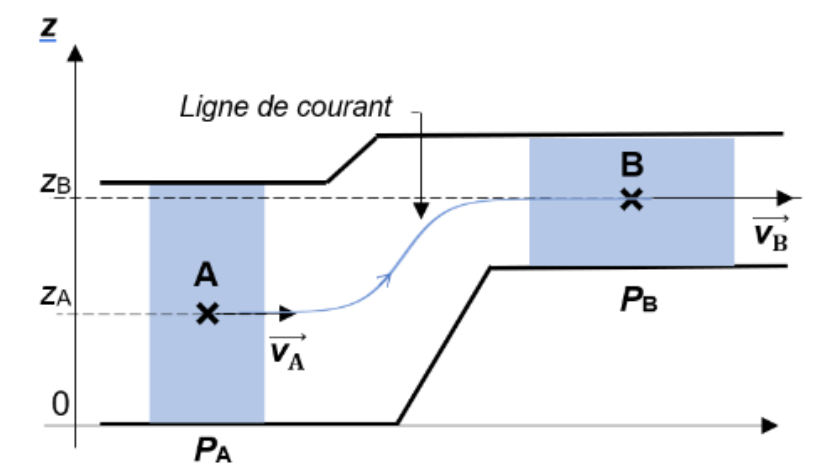
Figure 1 – Exemple de situation avec une ligne de courant représentée

1 mmHg correspond à la différence de pression entre deux points situés dans une colonne de mercure immobile et séparés d’une altitude de 1 millimètre.
En statique des fluides, dans la relation de Bernoulli : v_A = v_B = 0,00 m·s^–1.
Masse volumique du sang : r(sang) = 1,05 ×10³ kg·m^–3.
Masse volumique du mercure : r(Hg) = 13,6×10³ kg·m^–3.
Intensité de la pesanteur terrestre : g = 9,81 N·kg^–1.

Pour modéliser la situation d’une sténose aortique, on considère que la valve aortique est une succession de cylindres de diamètres dA et dB comme représentée figure 2.

On supposera ici que le sang est un fluide parfait en écoulement horizontal permanent.

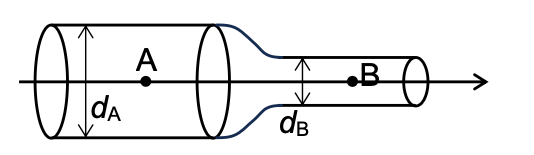
Figure 2 – Modélisation d’une valve aortique

1. À l’aide de la relation de Bernoulli appliquée à la statique des fluides, montrer que 1,00 mmHg correspond à une différence de pression de 133 Pa.

À l’aide de la relation de Bernoulli calculons une différence de pression :
$P_A+\frac{1}{2}\times\rho\times v_A^2+\rho\times g\times z_A=P_B+\frac{1}{2}\times\rho\times v_B^2+\rho\times g\times z_B$
$P_A-P_B=\frac{1}{2}\times\rho\times v_B^2+\rho\times g\times z_B-\frac{1}{2}\times\rho\times v_A^2-\rho\times g\times z_A$
$P_A-P_B=\frac{1}{2}\times\rho\times v_B^2-\frac{1}{2}\times\rho\times v_A^2+\rho\times g\times z_B-\rho\times g\times z_A$
$P_A-P_B=\frac{1}{2}\times\rho\times\left(v_B^2-v_A^2\right)+\rho\times g\times\left(z_B-z_A\right)$

D’après le sujet : « 1 mmHg correspond à la différence de pression entre deux points situés dans une colonne de mercure immobile et séparés d’une altitude de 1 millimètre. »
Immobile : $v_A=v_B=0\ m.s^{-1}$
Séparés d’une altitude de 1 millimètre : $z_B-z_A=1\ mm$
Colonne de mercure : $\rho=\rho\left(Hg\right)$

$P_A-P_B=\frac{1}{2}\times13,6\times10^3\times\left(0^2-0^2\right)+13,6\times10^3\times9,81\times\left(1\times10^{-3}\right)$
$P_A-P_B=133\ Pa$

Un rétrécissement aortique serré est défini par :

une vitesse maximale du sang de valeur supérieure à 4 m·s^–1 en sortie de valve aortique ;
une différence de pression supérieure à 50 mmHg à travers la valve aortique (selon les recommandations européennes) ;
et une surface de la section de la valve aortique au niveau du rétrécissement (point B) inférieure à 1 cm².

Lors d’un examen auprès d’un patient susceptible de présenter un rétrécissement aortique, on mesure, par échographie Doppler, les valeurs des vitesses de l’écoulement du sang aux points A et B situés sur une même ligne de courant. On obtient :

v_A = 1,0 m·s^–1 et v_B = 4,2 m·s^–1.

2. Déterminer la différence de pression P_A – P_B en pascals, puis en mmHg.

$P_A-P_B=\frac{1}{2}\times\rho\times\left(v_B^2-v_A^2\right)+\rho\times g\times\left(z_B-z_A\right)$
$z_A=z_B$
$P_A-P_B=\frac{1}{2}\times\rho\times\left(v_B^2-v_A^2\right)+\rho\times g\times\left(0\right)$
$P_A-P_B=\frac{1}{2}\times\rho\times\left(v_B^2-v_A^2\right)$
$P_A-P_B=\frac{1}{2}\times1,05\times10^3\times\left({4,2}^2-{1,0}^2\right)$
$P_A-P_B=8,7\times10^3\ Pa$

D’après la question précédente : 1,00 mmHg correspond à une différence de pression de 133 Pa

1,00 mmHg	133 Pa
$P_A-P_B$	$8,7\times10^3\ Pa$

$P_A-P_B=\frac{8,7\times10^3\times1,00}{133}$
$P_A-P_B=65\ mmHg$

Afin de déterminer la surface de la section de la valve aortique au niveau du rétrécissement (point B), on mesure par échographie le diamètre d_A à l’entrée de la valve aortique. Pour le patient précédent, on obtient : d_A = 20,2 mm.

3. Justifier, à l’aide des résultats et des données précédentes, que le patient analysé a un rétrécissement aortique serré.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti : la démarche est évaluée et nécessite d’être correctement présentée.

Un rétrécissement aortique serré est défini par :
– une vitesse maximale du sang de valeur supérieure à 4 m·s–1 en sortie de valve aortique ;
– une différence de pression supérieure à 50 mmHg à travers la valve aortique (selon les recommandations européennes) ;
– et une surface de la section de la valve aortique au niveau du rétrécissement (point B) inférieure à 1 cm2.

Calculons surface de la section de la valve aortique au niveau du rétrécissement (point B) :
Conservation du débit volumique :
$D_{V(B)}=D_{V(A)}$
$S_B\times v_B=S_A\times v_A$
$S_B=\frac{S_A\times v_A}{v_B}$

Or
$S_A=\pi\times r_A^2$
$S_A=\pi\times\left(\frac{d_A}{2}\right)^2$

D’où
$S_B=\frac{\pi\times\left(\frac{d_A}{2}\right)^2\times v_A}{v_B}$
$S_B=\frac{\pi\times\left(\frac{20,2\times10^3}{2}\right)^2\times1,0}{4,2}$
$S_B=7,6\times10^{-5}\ m^2$
$S_B=0,76\ cm^2$

Pour notre patient :
La vitesse maximale du sang de valeur supérieure à 4 m·s–1 car $v_B=4,2\ m.s^{-1}$
La différence de pression supérieure à 50 mmHg car $P_A-P_B=65\ mmHg$
La surface de la section de la valve aortique au niveau du rétrécissement (point B) inférieure à 1 cm2 : $S_B=0,76\ cm^2$

Les trois conditions sont remplies : le patient analysé a un rétrécissement aortique serré.

Partie B – Écoulement de Poiseuille

Le sang est un fluide réel et, dans divers cas, sa viscosité n’est pas négligeable.

Pour qu’un fluide réel s’écoule entre deux points, une différence de pression doit s’appliquer entre ces points.

Dans le cas d’un écoulement de Poiseuille dans une conduite cylindrique horizontale de longueur L et de diamètre d, la différence de pression DP est proportionnelle au débit volumique D_v du fluide dans la conduite :

$$|\Delta P|=R\times D_v \quad avec \quad R=\frac{64\times L\times \eta}{\pi\times d^4}$$

η est la viscosité du fluide, R la résistance à l’écoulement de la conduite et |Δ𝑃| est la valeur absolue de la variation de pression Δ𝑃.

On considère la situation simplifiée de la figure 3 ci-contre.

Du sang parcourt une artère, se divise dans un réseau de plusieurs millions de capillaires, supposés identiques et situés à une altitude voisine, puis rejoint une veine.

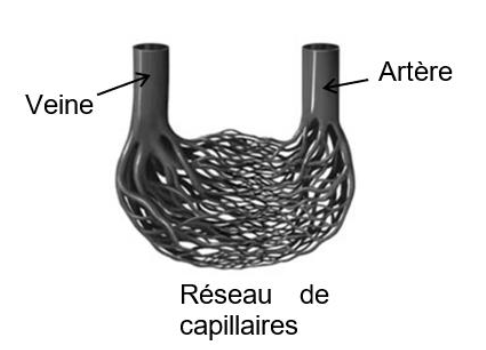
Figure 3 – Répartition du sang dans les capillaires

D’après www.concours-agro-veto.net

On considérera que la résistance à l’écoulement du sang est uniquement due aux capillaires.

Données :

Pression au sein de l’artère : P₁ = 16,0 × 10³ Pa.
Pression au sein de la veine : P₂ = 1,3 × 10³ Pa.
Résistance à l’écoulement d’un capillaire : R = 1,0×10¹⁶ S.I.

4. Expliquer pourquoi la résistance à l’écoulement du sang dans un capillaire est très supérieure à celle dans une artère ou dans une veine.

D’après le sujet la résistance à l’écoulement de la conduite est définie par :
$$R=\frac{64\times L\times\eta}{\pi\times d^4}$$
La résistance à l’écoulement est inversement proportionnelle au diamètre puissance 4.
Or le diamètre d’un capillaire est inférieur à celui d’une artère ou d’une veine.
Ainsi, la résistance à l’écoulement du sang dans un capillaire est très supérieure à celle dans une artère ou dans une veine.

5. Calculer le débit volumique du sang dans un capillaire.

$\Delta P=R\times D_v$
$R\times D_v=\Delta P$
$D_v=\Delta P R$
$D_v=\frac{\left|16,0\times10^3-1,0\times10^3\right|}{1,0\times10^{16}}$
$D_v=1,5\times10^{-12}\ m^3\cdot s^{-1}$

Dans l’artère, le débit volumique du sang est de 5 × 10^{– 6} m³·s^–1.

6. Montrer que le nombre N_C de capillaires parcourus par le sang est en accord avec la partie de phrase soulignée dans le texte introductif à gauche de la figure 3.

D’après le sujet : « Du sang parcourt une artère, se divise dans un réseau de plusieurs millions de capillaires, supposés identiques et situés à une altitude voisine, puis rejoint une veine. »

1 capillaire	$1,5\times10^{-12}\ m^3\cdot s^{-1}$
N_C capillaires	$5\times10^{-6}\ m^3\cdot s^{-1}$

Calculons le nombre de capillaires :

$N_c=\frac{5\times10^{-6}\times1}{1,5\times10^{-12}}$
$N_c=3,3\times10^6$

Il y’a 3,3 millions de capillaires.
Ainsi, le nombre $N_C$ de capillaires parcourus par le sang est en accord avec la partie de phrase soulignée dans le texte introductif à gauche de la figure 3 (plusieurs millions de capillaires).