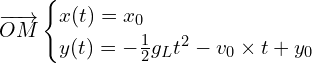Bac Centres étrangers 2021 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ1G11
Mots-clés : deuxième loi de Newton, mouvement dans un champ uniforme.
Au XVIIème siècle, Galilée a établi que la vitesse d’un objet en chute libre est indépendante de la masse de cet objet : lâchés avec des conditions initiales identiques, deux objets quelconques ont le même mouvement de chute libre.
Une vérification expérimentale spectaculaire a été réalisée sur la Lune par l’astronaute David Scott en 1971. Scott a utilisé un marteau et une plume qu’il a lâchés simultanément d’une même hauteur avec une vitesse initiale nulle. Les deux objets ont touché le sol lunaire au même instant.
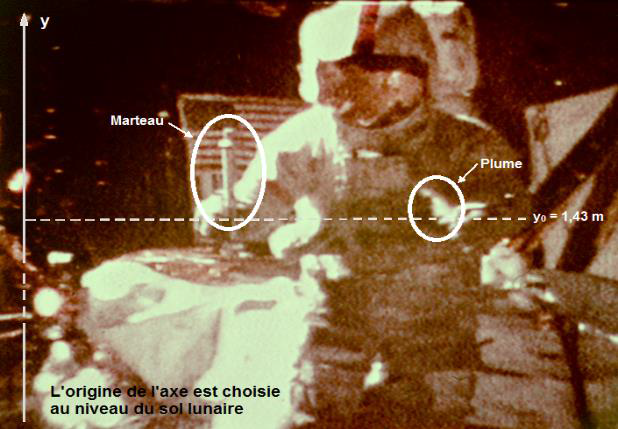
https://nssdc.gsfc.nasa.g
Outre cette vérification de la loi de la chute des corps, cette expérience permet également d’estimer la masse de la Lune en utilisant les lois de la mécanique de Newton.
L’objet de cet exercice est de retrouver la masse de la Lune en analysant le mouvement de l’un des deux corps lâchés par Scott. On s’intéresse au mouvement du système {marteau}.
Données
- Constante de gravitation universelle : G = 6,67 × 10−11 N ⋅ m2 ⋅ kg−2.
- Rayon de la Lune : R𝐿 = 1,74 × 106 m.
- Masse de la Lune : 𝑀𝐿 = 7,34 × 1022 kg.
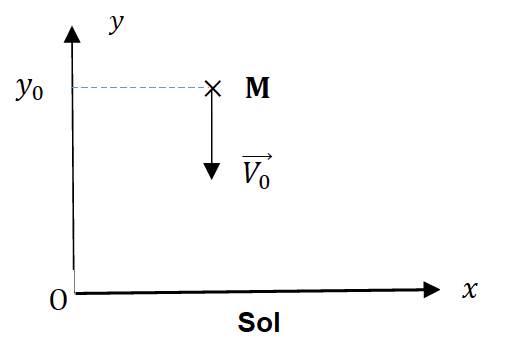
Le mouvement du centre de masse du marteau est étudié dans un référentiel lunaire supposé galiléen. L’origine du repère est choisie au niveau du sol lunaire.
Le pointage des positions du marteau débute à un instant choisi comme origine des dates lorsque le marteau se trouve à 1,43 m du sol. Il a alors une vitesse ![]() verticale, dirigée vers le bas.
verticale, dirigée vers le bas.
Le mouvement du marteau est vertical suivant l’axe (Oy).
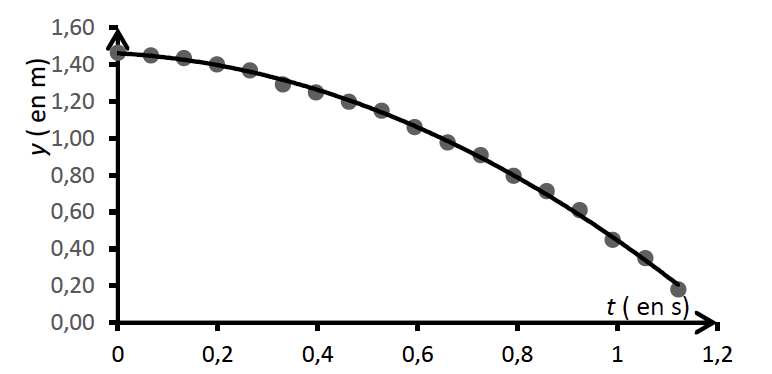
Le pointage des positions successives occupées par le marteau a permis de réaliser un graphe représentant ces positions, repérées par des points, en fonction du temps.
Le tableur utilisé permet de modéliser la courbe y = f(t) représentant l’évolution temporelle des positions par une parabole d’équation : y = At2+ Bt+C
avec :
- A = − 0,865 m⋅s−2,
- B = − 0,15 m⋅s−1,
- C = 1,43 m.
- y en mètre
- t en seconde
Questions préliminaires
1. Compte tenu de la faible valeur de la hauteur initiale, on considère que la distance entre le centre de la Lune et le marteau tout au long de sa chute est égale au rayon de la Lune R𝐿. Donner l’expression vectorielle de la force gravitationnelle ![]() modélisant l’action exercée par la Lune sur le marteau en fonction de la masse de la Lune 𝑀𝐿, de la masse du marteau 𝑚, du rayon de la Lune R𝐿 et d’un vecteur unitaire
modélisant l’action exercée par la Lune sur le marteau en fonction de la masse de la Lune 𝑀𝐿, de la masse du marteau 𝑚, du rayon de la Lune R𝐿 et d’un vecteur unitaire ![]() orienté du centre de la Lune vers la surface lunaire. Représenter cette force sur un schéma, sans souci d’échelle.
orienté du centre de la Lune vers la surface lunaire. Représenter cette force sur un schéma, sans souci d’échelle.
2. Par approximation, on peut assimiler le champ de gravitation lunaire ![]() à la surface de la Lune au champ de pesanteur sur la Lune
à la surface de la Lune au champ de pesanteur sur la Lune ![]() .
.
Montrer que l’expression du champ de pesanteur ![]() , au lieu où se trouve le marteau sur la Lune, s’écrit :
, au lieu où se trouve le marteau sur la Lune, s’écrit :
![]()
3. Montrer que, pendant la chute, le vecteur accélération du marteau ![]() vérifie :
vérifie :
![]()
Réponse :
Système {marteau}
Référentiel lunaire supposé galiléen
D’après la deuxième loi de newton :
![]()
![]()
![]()
![]()
Or
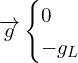
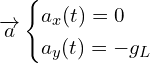
Problème à résoudre
En s’appuyant sur les questions préliminaires et sur la modélisation de l’évolution temporelle des positions fournie par le tableur, déterminer la masse de la Lune 𝑀𝐿.
L’analyse des données, la démarche suivie ainsi que les calculs doivent être correctement présentés et justifiés.
Un regard critique sera porté sur le résultat et des propositions seront faites sur les causes possibles d’un éventuel écart avec la valeur de référence fournie.
Le candidat est invité à présenter sa démarche même si elle n’est pas complètement aboutie.
Réponse :
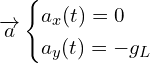
![]()
On intègre le système d’équation précédent :
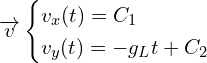
Pour trouver les constantes, on utilise ![]() :
:
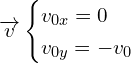
d’ou
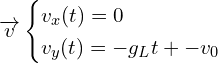
![]()
On intègre le système d’équation précédent :
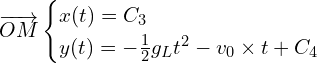
Pour trouver les constantes, on utilise ![]()
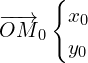
d’ou