Bac Centres étrangers 2024 Sujet 1
Exercice 3 – (6 points) – Durée 1h03 – Calculatrice autorisée
Sujet n° 24-PYCG22BIS
Sujet et corrigé
EXERCICE 3 – DÉTERMINATION DE LA VALEUR DU CHAMP DE PESANTEUR À LA SURFACE DE LA LUNE (6 points)
Apollo 14 (31 janvier 1971 – 9 février 1971) est la huitième mission habitée du programme Apollo et la troisième à se poser sur la Lune. Il s’agit de la première mission dont le lieu d’atterrissage a été sélectionné non en fonction de contraintes techniques, mais pour son intérêt géologique.
(https://fr.wikipedia.org/wiki/Apollo_14)
Le 6 février 1971, l’astronaute Alan Shepard s’essaya au golf à la surface de la Lune. Après deux tentatives infructueuses du fait de la gêne créée par sa combinaison spatiale, le troisième essai propulsa la balle de telle sorte qu’elle ne fut retrouvée qu’en 2021, grâce à une analyse numérique poussée du film original de la mission. Il fut alors établi que la balle n’avait pas parcouru des kilomètres et des kilomètres, mais seulement 36 m ! (https://sciencepost.fr/balle-de-golf-alan-shepard-lune-apollo-14/)
À partir des informations disponibles sur ce tir, il a aussi été possible d’estimer que la balle était partie avec une vitesse initiale 𝑉0 = 30 km ⋅ h−1 et avec un angle initial 𝜃 = 25°.
L’objectif de cet exercice est de montrer que les caractéristiques de ce tir permettent d’obtenir une estimation de la valeur du champ de pesanteur à la surface de la Lune, noté 𝑔L.
La balle de golf est modélisée par un point matériel de masse 𝑚 = 46,0 g évoluant dans le champ de pesanteur lunaire 𝑔⃗⃗⃗L. Du fait de l’absence d’air, la balle ne subit aucune force autre que son poids.
Le mouvement de la balle est étudié dans le système d’axes (Ox ; Oy). À la date 𝑡 = 0 s, elle est placée à l’origine du repère O.
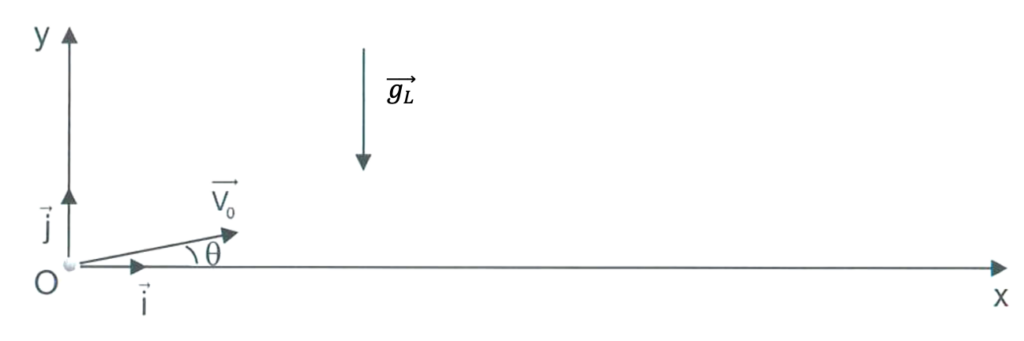
Étude du mouvement et détermination du champ de pesanteur lunaire
Q1. À partir d’une loi dont on donnera le nom, exprimer les composantes du vecteur accélération $\overrightarrow{a}$ dans le repère (Ox ; Oy).
Système {balle de golf}
Référentiel sol lunaire supposé galiléen
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{P}=m\overrightarrow{a}$$
$$m\overrightarrow{g_L}=m\overrightarrow{a}$$
$$\overrightarrow{g_L}=\overrightarrow{a}$$
Or
$$\overrightarrow{g_L}\begin{pmatrix}0 \\ -g_L\end{pmatrix}$$
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$\overrightarrow{a}\begin{pmatrix}a_x(t)=0 \\ a_y(t)=-g_L\end{pmatrix}$$
Q2. En déduire les équations horaires 𝑥(𝑡) et 𝑦(𝑡) du mouvement de la balle.
$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=C_1 \\ v_y(t)=-g_L \times t + C_2\end{pmatrix}$$
Pour trouver les constantes, on utilise $\overrightarrow{v_0}$
$$\overrightarrow{v_0}\begin{pmatrix}v_{0x}=v_0 \times \cos(\theta) \\ v_{0y}=v_0 \times \sin(\theta)\end{pmatrix}$$
d’ou
$$\overrightarrow{v}\begin{pmatrix}v_x(t)=v_0 \times \cos(\theta) \\ v_y(t)=-g_L \times t + v_0 \times \sin(\theta)\end{pmatrix}$$
$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0 \times \cos(\theta) \times t + C_3 \\ y(t)=-\frac{1}{2}\times g_L \times t^2 + v_0 \times \sin(\theta) \times t + C_4\end{pmatrix}$$
Pour trouver les constantes, on utilise $\overrightarrow{OG_0}$
$$\overrightarrow{OG_0}\begin{pmatrix}x_0=0 \\ y_0=0\end{pmatrix}$$
d’ou
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0 \times \cos(\theta) \times t \\ y(t)=-\frac{1}{2}\times g_L \times t^2 + v_0 \times \sin(\theta) \times t\end{pmatrix}$$
La portée du tir correspond à la distance 𝑥P entre l’origine du mouvement O et le point d’impact au sol. La durée du vol, 𝑡vol, est le temps écoulé entre le tir et le moment où la balle retombe au sol.
Q3. À partir des équations horaires du mouvement établies à la question Q2, montrer, en détaillant soigneusement le raisonnement, que 𝑡vol, la durée du vol de la balle, peut s’exprimer :
$$ t_{vol}=\frac{2\times v_0\times\sin(\theta)}{g_L} $$
La durée $t_{vol}$ est la durée nécessaire pour que le système atteigne le sol : $y(t_{vol})=0$
$$y(t_{vol})=-\frac{1}{2}\times g_L \times t_{vol}^2 + v_0 \times \sin(\theta) \times t_{vol}$$
$$0=-\frac{1}{2}\times g_L \times t_{vol}^2 + v_0 \times \sin(\theta) \times t_{vol}$$
$$0=\left(-\frac{1}{2}\times g_L \times t_{vol}+v_0 \times \sin(\theta)\right)\times t_{vol}$$
Un produit de facteur est nul si et seulement si un de ses facteur est nul :
$t_{vol}=0\ s$ qui correspond au temps du départ
$$-\frac{1}{2}\times g_L \times t_{vol}+v_0 \times \sin(\theta)=0$$
$$-\frac{1}{2}\times g_L \times t_{vol}=-v_0 \times \sin(\theta)$$
$$\frac{1}{2}\times g_L \times t_{vol}=v_0 \times \sin(\theta)$$
$$t_{vol}=\frac{2\times v_0 \times \sin(\theta)}{g_L}$$
Q4. À partir des mêmes équations horaires du mouvement, déterminer une autre expression du temps de vol 𝑡vol en fonction de la portée du tir 𝑥P, de la vitesse initiale de la balle 𝑉0, et de l’angle de tir 𝜃.
La durée $t_{vol}$ est la durée nécessaire pour que le système atteigne le sol : $x(t_{vol})=x_p$
$$x(t_{vol})=v_0 \times \cos(\theta) \times t_{vol}$$
$$x_p=v_0 \times \cos(\theta) \times t_{vol}$$
$$v_0 \times \cos(\theta) \times t_{vol}=x_p$$
$$t_{vol}=\frac{x_p}{v_0 \times \cos(\theta)}$$
Q5. En déduire, en détaillant le raisonnement, que l’expression du champ de pesanteur lunaire 𝑔L peut s’écrire :
$$ g_L=\frac{2\times v_0^2\times\cos(\theta)\times\sin(\theta)}{x_p} $$
Les deux temps de vol trouvés aux Q3 et Q4 sont égaux :
$$t_{vol}=\frac{2\times v_0 \times \sin(\theta)}{g_L}$$
$$t_{vol}=\frac{x_p}{v_0 \times \cos(\theta)}$$
Ainsi :
$$\frac{2\times v_0 \times \sin(\theta)}{g_L}=\frac{x_p}{v_0 \times \cos(\theta)}$$
$$\frac{g_L}{2\times v_0 \times \sin(\theta)}=\frac{v_0 \times \cos(\theta)}{x_p}$$
$$g_L=\frac{v_0 \times \cos(\theta)\times 2\times v_0 \times \sin(\theta)}{x_p}$$
$$g_L=\frac{2\times v_0^2 \times \cos(\theta)\times \sin(\theta)}{x_p}$$
On suppose que la balle s’est arrêtée là où elle a touché le sol (elle n’a pas roulé). Autrement dit :
𝑥P = 36 m
Q6. Calculer la valeur numérique de 𝑔L en précisant son unité.
$$g_L=\frac{2\times v_0^2 \times \cos(\theta)\times \sin(\theta)}{x_p}$$
$$g_L=\frac{2\times\left(\frac{30}{3,6}\right)^2\times \cos(25)\times \sin(25)}{36}$$
$$g_L=1,5\ m.s^{-2}$$
On souhaite comparer cette valeur à celle obtenue à partir des caractéristiques de la Lune en appliquant la loi de la gravitation universelle. Cette dernière permet d’exprimer le champ de pesanteur lunaire 𝑔L0 en fonction de la constante de gravitation universelle 𝐺, de la masse de la Lune 𝑀L et du rayon de la lune 𝑅L selon l’expression :
$$ g_L=\frac{2\times v_0^2\times\cos(\theta)\times\sin(\theta)}{x_p} $$
Q7. Calculer la valeur numérique de 𝑔L0 en utilisant les données ci-après.
- Masse de la Lune : 𝑀L = 7,34 × 1022 kg
- Rayon de la lune : 𝑅L = 1740 km
- Constante de gravitation universelle : 𝐺 = 6,67 × 10−11 m3 ∙ kg−1 ∙ s−2
$$g_{L0}=\frac{G\times M_L}{R_L^2}$$
$$g_{L0}=\frac{6,67\times 10^{-11}\times 7,34\times 10^{22}}{\left(1740\times 10^3\right)^2}$$
$$g_{L0}=1,62\ m.s^{-2}$$
Q8. Comparer la valeur du champ de pesanteur lunaire 𝑔L0 obtenue à partir de la loi de gravitation universelle à celle obtenue à partir du tir de golf d’Alan Shepard.
La valeur du champ de pesanteur lunaire $g_{L0}$ obtenue à partir de la loi de gravitation universelle et celle obtenue à partir du tir de golf d’Alan Shepard sont proches.
