Centres étrangers 2022 Sujet 2
Exercice A – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ2G11
Sujet et corrigé
Mots clés: lunette afocale, grossissement
Dans cet exercice, on se propose d’examiner comment il a été possible historiquement de déterminer le diamètre de la planète Jupiter grâce à des observations réalisées avec des lunettes astronomiques.
La distance entre la Terre et Jupiter étant connue, il est possible de déterminer le diamètre D de Jupiter si on connait son diamètre apparent αJ vu à l’œil nu depuis la Terre (Figure 1 ci- dessous).
Le diamètre apparent de Jupiter αJ a été déterminé par le physicien néerlandais Huygens.
DOCUMENT : observations de Jupiter par Huygens en juin 1684.
Dans un premier temps, Huygens raconte qu’avec le grossissement utilisé, il voyait Jupiter à travers la lunette deux fois plus gros qu’il ne voyait la Lune à l’œil nu. Il estimait le grossissement de sa lunette à 164. Le diamètre apparent de la Lune à l’œil nu étant connu, il put estimer que celui de Jupiter était approximativement αJ = 10-4 radians.

Christian Huygens
(1629-1695)
Une semaine après, il imagina un dispositif permettant de déterminer plus précisément la valeur du diamètre apparent de Jupiter qu’il avait seulement estimée. Pour cela, Huygens eut l’idée d’insérer dans sa lunette, au niveau de l’image intermédiaire de Jupiter créée par l’objectif, un petit repère lui permettant alors de mesurer la taille de l’image intermédiaire. Il mesura ainsi l’image intermédiaire de Jupiter et trouva 2 millimètres. À partir de cette valeur, il put calculer le diamètre apparent de Jupiter et trouva 2·10-4 radians.
Le diamètre apparent 𝜶 d’un objet de diamètre AB = D est défini comme étant l’angle sous lequel il est observé.

Figure 1.
- Notations : on note 𝛼 l’angle sous lequel on voit l’objet à l’œil nu et 𝛼′ l’angle sous lequel on voit ce même objet à travers la lunette.
- Dans l’ensemble de cet exercice, tous les angles sont petits. Pour de tels angles, il est possible d’écrire tan 𝛼 = 𝛼 si 𝛼 est en radians.
Estimation du diamètre apparent de Jupiter αJ par comparaison avec la Lune
1. Rappeler la définition du grossissement G de la lunette en fonction de 𝛼 et 𝛼′.
$$G = \frac{\alpha^\prime}{\alpha}$$
2. En reprenant le premier paragraphe du DOCUMENT, montrer que :
$a_J= \frac{2 \alpha_L}{G}$
αJ étant le diamètre apparent de Jupiter, G le grossissement de la lunette et αL le diamètre apparent de la Lune à l’œil nu.
« Il voyait Jupiter à travers la lunette deux fois plus gros qu’il ne voyait la Lune à l’œil nu »
$\alpha_J^\prime = 2\alpha_L$
Or $G = \frac{\alpha_J^\prime}{\alpha_J}$
$$\alpha_J^\prime = G \times \alpha_J$$
Donc :
$$G \times \alpha_J = 2\alpha_L$$
$$\alpha_J = \frac{2\alpha_L}{G}$$
Huygens connaissait la valeur du diamètre apparent de la Lune à l’œil nu :
αL = 0,5°= 8,7 x 10-3 rad
3. Montrer que l’on retrouve la valeur du diamètre apparent de Jupiter trouvée dans un premier temps par Huygens.
$$\alpha_J = \frac{2\alpha_L}{G}$$
$$\alpha_J = \frac{2 \times 8,7 \times 10^{-3}}{164}$$
$$\alpha_J = 1,1 \times 10^{-4}\ rad$$
On retrouve $\alpha_J = 10^{-4}$ radians.
Modélisation de la lunette astronomique de Huygens
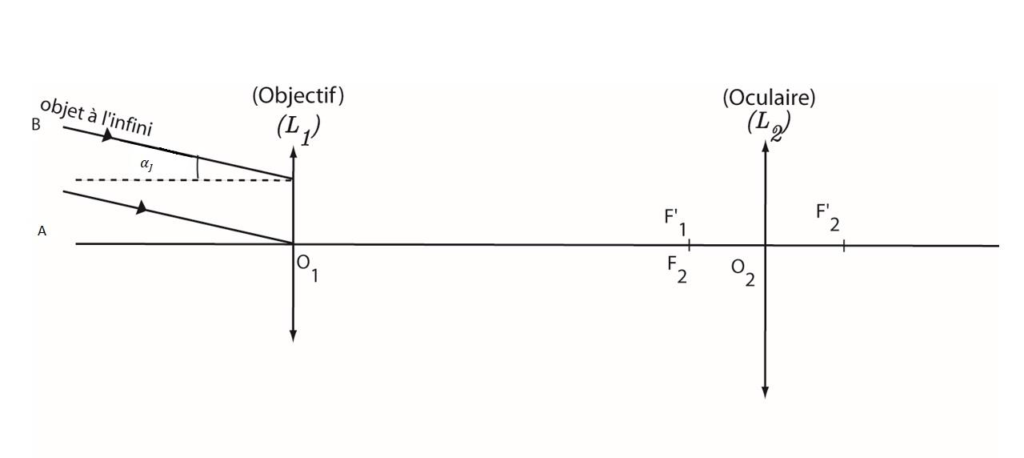
Afin de pouvoir exploiter la démarche présentée dans le deuxième paragraphe du DOCUMENT, et pour retrouver la valeur du grossissement de la lunette estimée par Huygens, on modélise la lunette astronomique par l’association d’une lentille convergente L1 de grande distance focale 𝑓’1 , appelée objectif et d’une lentille convergente L2 de petite distance focale 𝑓’2 , appelée oculaire.
Les deux lentilles sont placées de telle sorte que le foyer image F’1 de L1 coïncide avec le foyer objet 𝐹2 de L2. (Voir annexe page 15/15 à rendre avec la copie). L’ensemble des deux lentilles constitue un système afocal. Pour un tel système, l’image d’un objet situé à l’infini est située à l’infini.
On considère un objet AB situé « à l’infini », celui-ci représentant la planète Jupiter (Voir annexe page 15/15 à rendre avec la copie).
- Le point A est situé sur l’axe optique. Les rayons qui arrivent de A sont parallèles à l’axe optique.
- Le point B est situé hors axe optique. Les rayons issus de B sont parallèles entre eux et atteignent la lentille avec une inclinaison 𝛼𝐽 par rapport à l’axe optique.
4. Indiquer où se forme l’image intermédiaire A1B1 de l’objet AB formée par l’objectif. Justifier que l’ensemble des deux lentilles constitue effectivement un système afocal.
La lentille L1 donne de l’objet AB situé à l’infini une image $A_1B_1$ sur le foyer image $F_1^\prime$.
« Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini. »
Les deux foyers $F_1^\prime$ et $F_2$ sont confondus, ainsi la lentille L2 donne de l’objet $A_1B_1$ une image à l’infini.
La lunette est donc afocale.
Sur la figure donnée en annexe page 15/15 à rendre avec la copie :
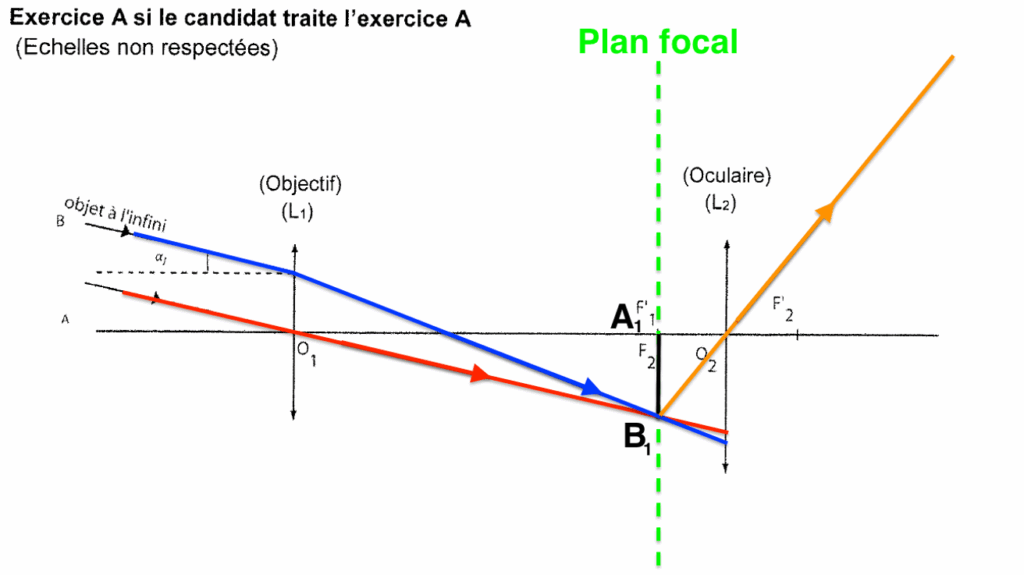
5. Construire l’image intermédiaire A1B1 de l’objet AB, situé « à l’infini », à travers la lentille L1.
Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 n’est pas dévié.
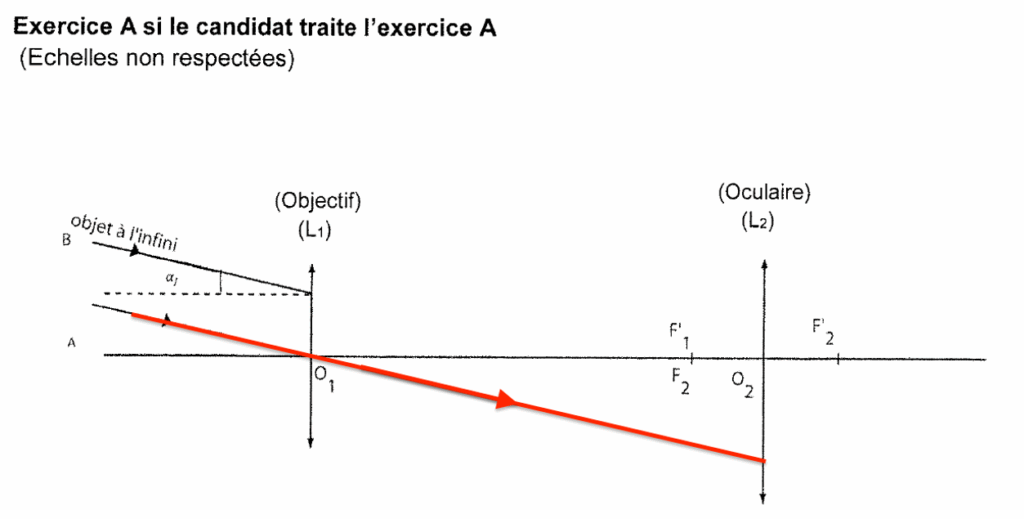
Position de B1 image intermédiaire de B : Comme l’objet AB est à l’infini, son image A1B1 est dans le plan focal image de l’objectif L1.
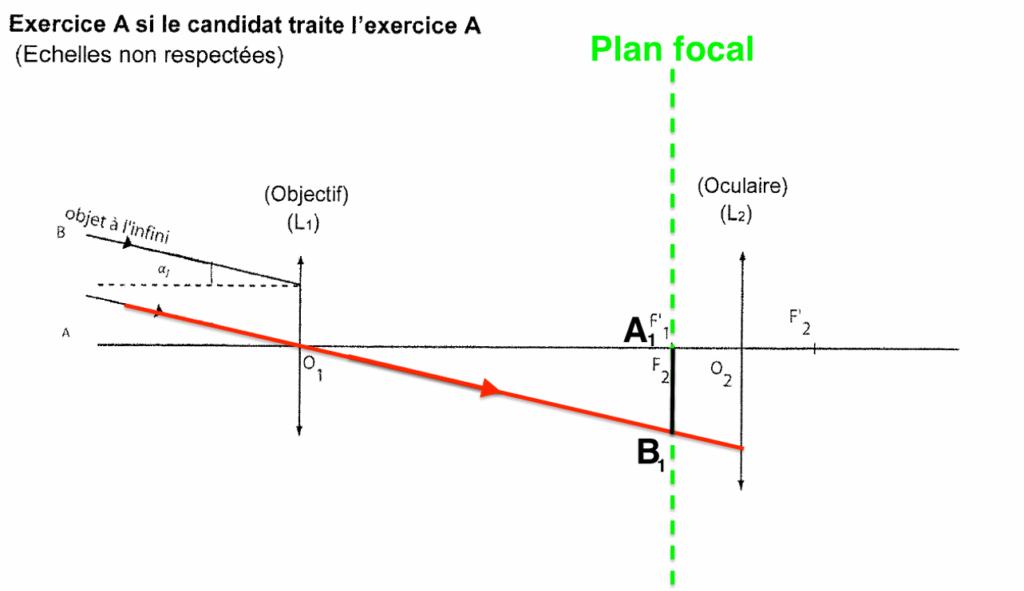
L’autre rayon lumineux issu de B est dévié vers B1.
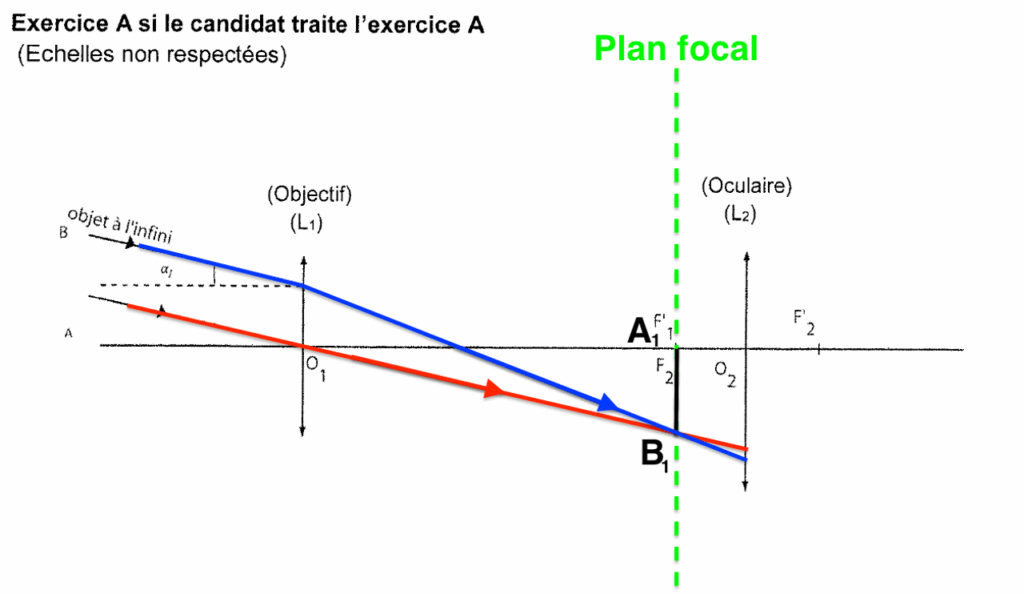
6. Représenter le faisceau émergent issu de B, situé « à l’infini », délimité par les deux rayons incidents déjà tracés, et traversant l’ensemble de la lunette afocale.
Pour les rayons émergeants de la lentille L2 :
- On trace un rayon issu de B1 passant par O2. Ce rayon ne sera pas dévié.
- De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L2 issue de B1 seront parallèles à ce rayon tracé.
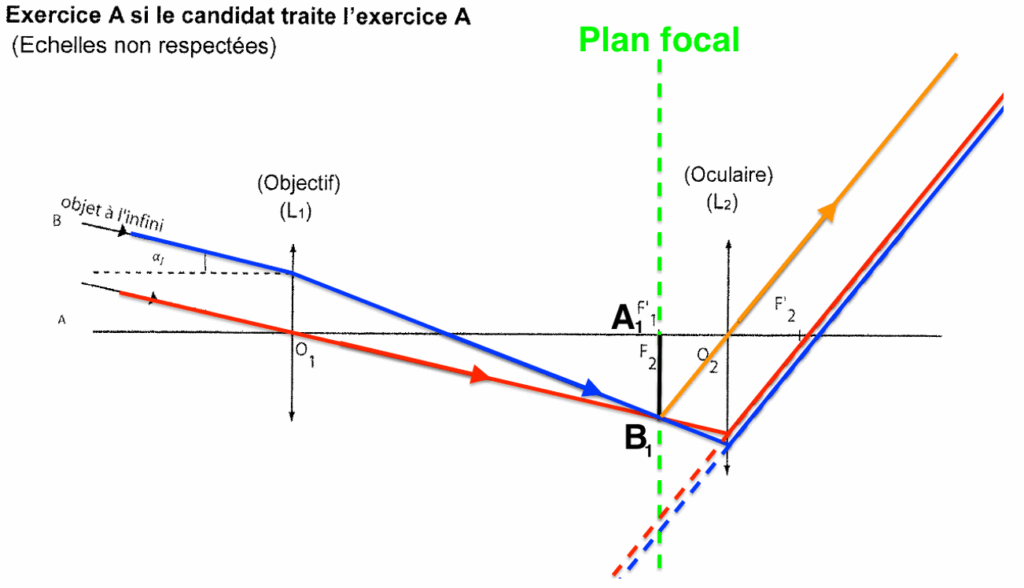
Le faisceau émergent (en sortie de l’oculaire) est incliné d’un angle 𝛼′ par rapport à l’axe optique.
7. Par des considérations géométriques, déterminer l’expression du grossissement G en fonction des distances focales 𝑓’1 et 𝑓’2.
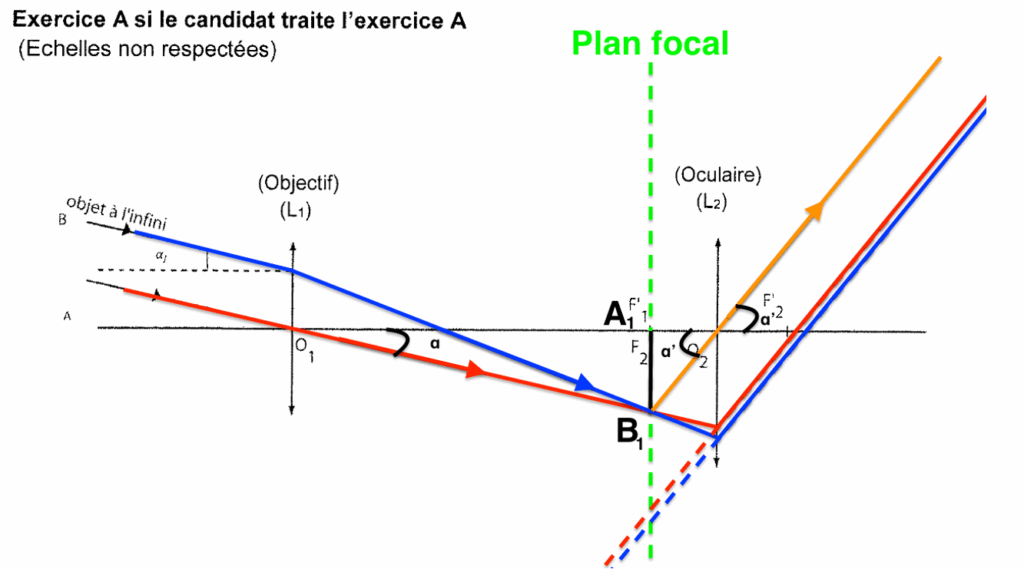
$$\tan(\alpha) \approx \alpha = \frac{A_1B_1}{f_1^\prime}$$
$$\tan(\alpha^\prime) \approx \alpha^\prime = \frac{A_1B_1}{f_2^\prime}$$
$$G = \frac{\alpha^\prime}{\alpha} = \frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}} = \frac{A_1B_1}{f_2^\prime} \times \frac{f_1^\prime}{A_1B_1} = \frac{f_1^\prime}{f_2^\prime}$$
$$G = \frac{f_1^\prime}{f_2^\prime}$$
Application à la lunette de Huygens
Les caractéristiques de la lunette de Huygens sont :
- Distance focale de l’objectif 𝑓’1= 10,35 m.
- Distance focale de l’oculaire 𝑓’2= 63 mm.
8. Expliquer le calcul effectué par Huygens, dans le deuxième paragraphe du DOCUMENT, pour obtenir la valeur de l’angle 𝛼𝐽 à partir de la taille de l’image intermédiaire.
$$\tan(\alpha_J) \approx \alpha_J = \frac{A_1B_1}{f_1^\prime}$$
$$\alpha_J = \frac{2 \times 10^{-3}}{10,35}$$
$$\alpha_J = 1,9 \times 10^{-4}\ rad$$
9. Calculer le grossissement de la lunette de Huygens et expliquer pour quelle raison la première détermination de 𝛼𝐽 présentée dans le premier paragraphe du DOCUMENT était nécessairement moins précise que celle présentée dans le second paragraphe.
$$G = \frac{f_1^\prime}{f_2^\prime}$$
$$G = \frac{10,35}{63 \times 10^{-3}}$$
$$G = 164$$
La détermination de $\alpha_J$ dans le deuxième paragraphe s’appuie sur la taille de l’image intermédiaire et la distance focale.
Ces deux valeurs se mesurent avec précision.
Dans le premier paragraphe, Huygens estime $\alpha_J$ à partir du diamètre apparent de la Lune.
Cette estimation est nécessairement moins précise que celle présentée dans le second paragraphe.
Diamètre de Jupiter
La distance Terre-Jupiter était connue à l’époque de Huygens. Cette distance a pour valeur moyenne 𝑑 = 7,80 x 108 km.
10. Calculer la valeur D du diamètre de Jupiter.
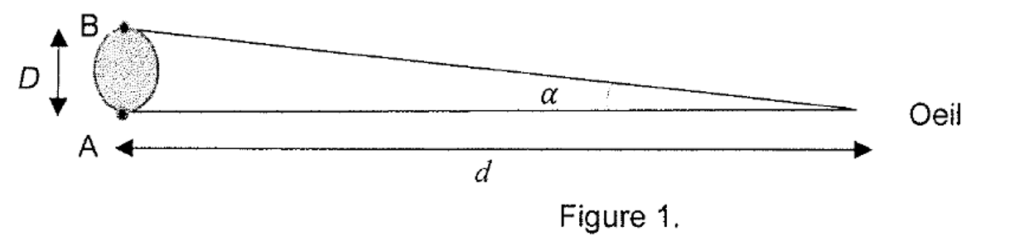
$$\tan(\alpha_J) \approx \alpha_J = \frac{D}{d}$$
$$\alpha_J = \frac{D}{d}$$
$$\alpha_J \times d = D$$
$$D = \alpha_J \times d$$
$$D = 1,9 \times 10^{-4} \times 7,80 \times 10^8$$
$$D = 1,5 \times 10^5\ km$$
annexe page 15/15 à rendre avec la copie
(Echelles non respectées)