Diamant et kimberlite

Enseignement scientifique première

Durée 1h – 10 points – Thème « Une longue histoire de la matière »

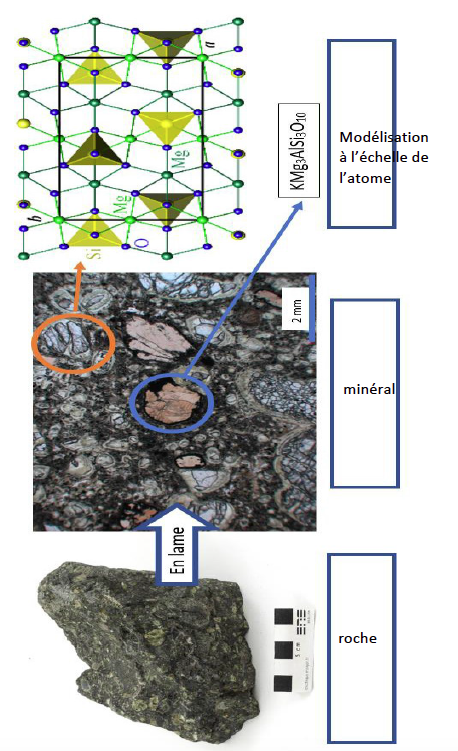
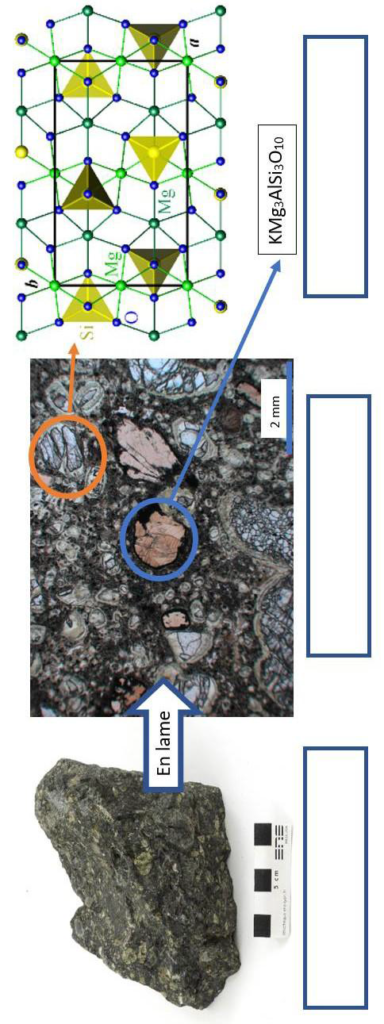
La kimberlite est une roche qui peut contenir des cristaux de diamant. Elle est issue du refroidissement d’une lave et doit son nom à la ville de Kimberley en Afrique du sud, où elle fut découverte pour la première fois.

Observation de la kimberlite

La kimberlite est présentée à différentes échelles sur le document réponse en annexe.

1 – Identifier les structures observées en inscrivant, parmi les propositions suivantes, les réponses dans les cadres prévus : « cellule », « roche », « organite », « minéral », modélisation à l’échelle de l’atome ».

2 – Cocher la proposition juste dans le QCM du document réponse à rendre avec la copie.

Un refroidissement rapide

Structure cristalline du diamant

Des diamants sont souvent présents dans la kimberlite sous forme d’inclusions. Le diamant est un minéral transparent composé de cristaux de carbone pur. Cette « pierre précieuse » est connue pour être le minéral le plus dur qui soit.

On cherche à savoir si, dans le cas du diamant, le carbone cristallise sous une forme cubique à face centrée.

Données :

Rayon d’un atome de carbone : 𝑟 = 70 pm.
Masse d’un atome de carbone : m = 2,0 x 10^-26 kg.

3. Étude d’un réseau cubique à faces centrées.

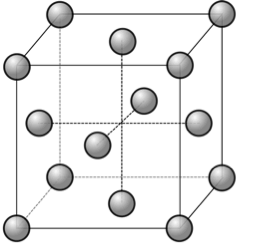
3-a Compléter le schéma de maille d’un réseau cubique à faces centrées présenté dans le document réponse en indiquant la position des atomes.

3-b Déterminer, en le justifiant, le nombre d’atomes présents à l’intérieur d’une maille.

Il y a 8 atomes sur les sommets qui sont dans 1/8 de la maille.

Il y a 6 atomes sur les faces qui sont dans 1/2 de la maille.

N=8×1/8+6×1/2=4

Il y a 4 atomes dans une maille.

Document 1. Vue d’une face du cube (réseau cubique à faces centrées)

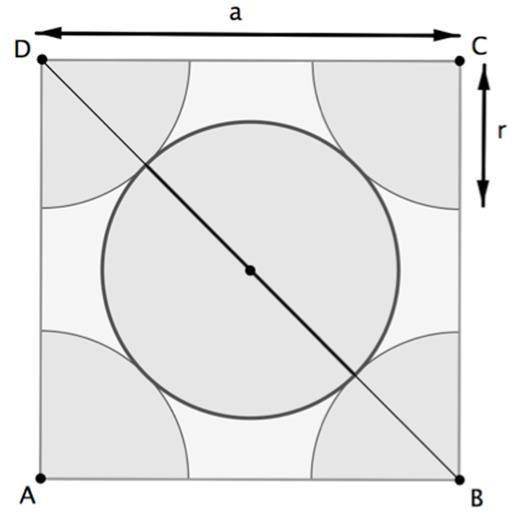
3-c Le paramètre de maille, noté a, est la longueur d’une arête du cube. Démontrer que a = 2√2𝑟.

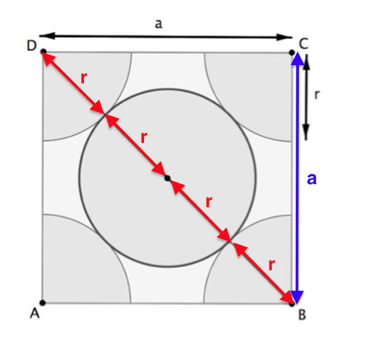
D’après le théorème de Pythagore :

$\left(4r\right)^2=a^2+a^2$

$16r^2=2a^2$

$2a^2=16r^2$

$a^2=\frac{16}{2}r^2$

$a^2=8r^2$

$a=\sqrt{8r^2}$

$a=2\sqrt{2}r$

3-d Montrer que la masse volumique 𝜌 qu’aurait le diamant, s’il possédait une structure cubique à faces centrées, vérifierait approximativement la formule

$\rho=0,18 \times \frac{m}{r^3}$

(avec m la masse d’un atome de carbone et r le rayon d’un atome de carbone modélisé par une sphère).

$\rho =\frac{m_{maille}}{V_{maille}}$

$m_{maille} =N \times m$

$V_{maille}=a^3$

$\rho =\frac{N \times m}{a^3}$

$\rho =\frac{4 \times m}{(2\sqrt{2}r)^3}$

$\rho =\frac{4 \times m}{16\sqrt{2}r^3}$

$\rho =\frac{4}{(16\sqrt{2}} \times \frac{ m}{r^3}$

$\rho =0,18 \times \frac{m}{r^3}$

4- La masse volumique du diamant est 3,51 x 103 kg.m-3. Indiquer si le diamant possède une structure cubique à faces centrées.

$\rho =0,18 \times \frac{m}{r^3}$

$\rho =0,18 \times \frac{2,0 \times10^{-26}}{(70 \times10^{-12})^3}$

$\rho =1,04 \times10^{4} Kg.m^{-3}$

La masse volumique du diamant est 3,51 x 10³ kg.m^-3 : elle est différente de celle calculée si le diamant possédait une structure cubique à faces centrées.

Le diamant ne possède pas une structure cubique à faces centrées.

Recherche de la profondeur de formation du diamant

Le carbone pur est présent dans la nature sous deux formes principales : le diamant, qui est transparent, et le graphite, qui est gris et opaque. En laboratoire, il est possible de fabriquer artificiellement du diamant à partir du graphite en modifiant les paramètres de pression et de température : le diamant peut être produit si la pression est comprise entre 5 et 12 GPa (sachant que 1 GPa = 1 x 10⁹Pa).

Document 2. Pression en fonction de la profondeur sous la surface terrestre

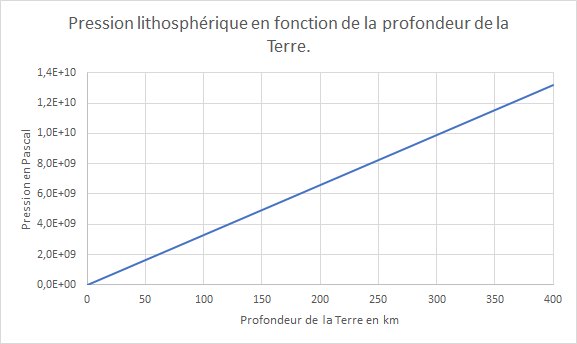
5- À l’aide du document 2, estimer la profondeur minimale à partir de laquelle les diamants peuvent se former.

Le diamant peut être produit si la pression est comprise entre 5 et 12 GPa (sachant que 1 GPa = 1 x 10⁹ Pa).

Au minimum la pression vaut 5 GPa = 5 x 10⁹ Pa

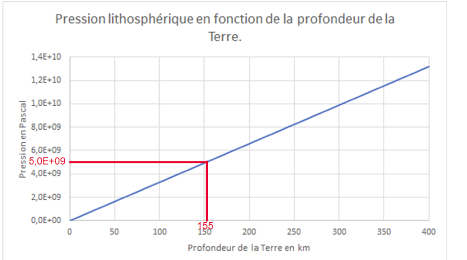
Graphiquement : la profondeur minimale à partir de laquelle les diamants peuvent se former est de 155 km.

Document réponse à rendre avec la copie

Diamant et kimberlite

Observation d’une kimberlite à différentes échelles

Question 2 (QCM)

Cocher la proposition exacte ci-dessous.

Lorsque les minéraux sont présents dans une pâte amorphe. Cela indique :

□ Un refroidissement rapide

□ Une forte pression

□ Un refroidissement lent

□ Une oxydation

Question 3a. Position des atomes dans la maille d’un réseau cubique à faces centrées

Compléter le schéma en indiquant la position des atomes de carbone dans la maille d’un réseau cubique à faces centrées.