Polynésie 2022 Sujet 1
Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 22-PYCJ1P01
Sujet et corrigé
Mots-clés : modèle optique, lunette astronomique, grossissement, diamètre apparent
Les scientifiques ont développé différents instruments d’optique telle que la lunette astronomique.
Dans cet exercice, nous allons nous intéresser au fonctionnement d’une lunette astronomique commerciale utilisée lors de l’observation de l’éclipse solaire du 10 juin 2021, l’observation du phénomène s’étant faite avec des lunettes de protection afin de ne pas altérer la vue.
Les objectifs de cet exercice sont de déterminer le grossissement de la lunette astronomique utilisée par un amateur lors de l’observation de l’éclipse solaire du 10 juin 2021 et de déterminer le diamètre approximatif de la Lune.
La lunette astronomique est un instrument afocal composé d’un tube principal contenant, à chacune de ses extrémités, une lentille convergente.
Le principe de cet instrument est de collecter la lumière émise par les astres, de la concentrer et de renvoyer à l’oeil une image agrandie de l’objet observé.
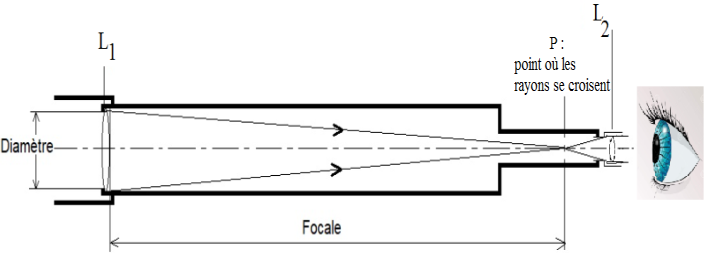
La figure 1 présente de façon simple la lunette de Galilée.
La lunette astronomique
1. Associer aux lentilles L1 et L2 les termes d’objectif et d’oculaire.
L1 : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet
L2 : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.
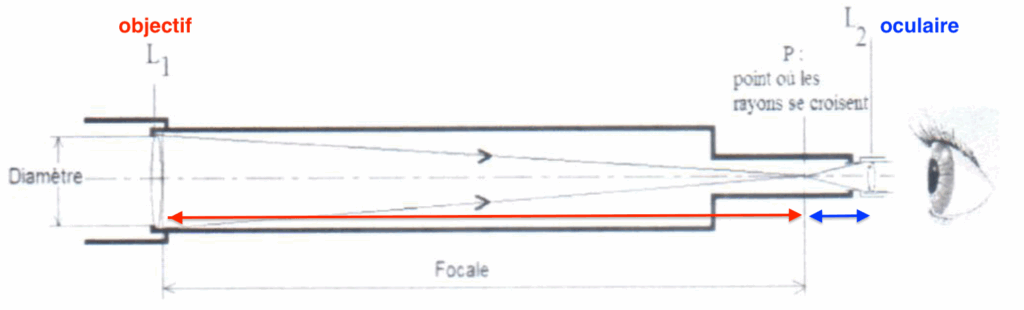
2. Pour la lentille L1, donner le nom scientifique du point P où les rayons se croisent.
Le nom du point $P$ où les rayons se croisent est le foyer image $F_1^\prime$ de la lentille $L_1$.
Données :
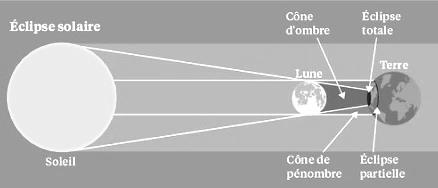
- L’éclipse solaire du 10 juin 2021 :
une éclipse solaire consiste en l’alignement des centres du Soleil, de la Lune et de la Terre. Le 10 juin 2021, la Lune s’est intercalée entre le Soleil et la Terre conformément à la figure ci-contre.
D’après : https://www.la-croix.com/Sciences-et-ethique/Sciences/Eclipse-quand-astre-cache-autre-2019-01-05-1200993316
Notice d’informations de la lunette astronomique utilisée lors de l’observation :
« La lunette informatisée utilisée est le compagnon idéal pour vos premières observations : la surface lunaire, Vénus et ses phases, Mars, Jupiter et ses 4 lunes, Saturne avec ses anneaux bien visibles et bien plus grâce à sa base de données intégrées dans la raquette de commande pour plus de 4 000 objets. Elle peut également être utilisée comme une longue-vue. »
Données techniques :
| Désignation | Lunette utilisée |
| Construction optique | Lentilles |
| Diamètre de l’objectif (en mm) | 102 |
| Focale de l’objectif (en cm) | 66 |
| Focale de l’oculaire (en mm) | 9,0 |
| Grossissement maximal | 73 × |
| Référence | ACEC298 |
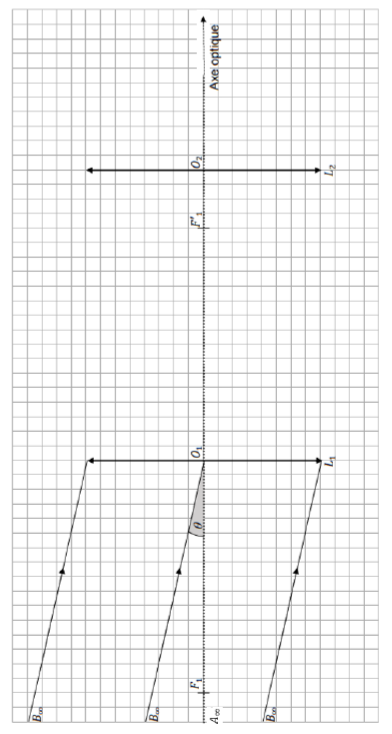
Le document réponse à rendre avec la copie représente l’observation de la Lune avec la lunette astronomique commerciale utilisée lors de l’éclipse du 10 juin 2021. Ce document est représenté sans souci d’échelle. La Lune, située à l’infini, est représentée par l’objet A∞B∞.
3. La lunette commerciale utilisée est afocale. Positionner, sur le document réponse à rendre avec la copie, le foyer principal objet F2 et le foyer principal image F2‘ de la lentille L2, sans souci d’échelle.
La lunette est afocale donc les deux foyers $F_1^\prime$ et $F_2$ sont confondus.
De plus $O_2F_2 = O_2F_2^\prime$.
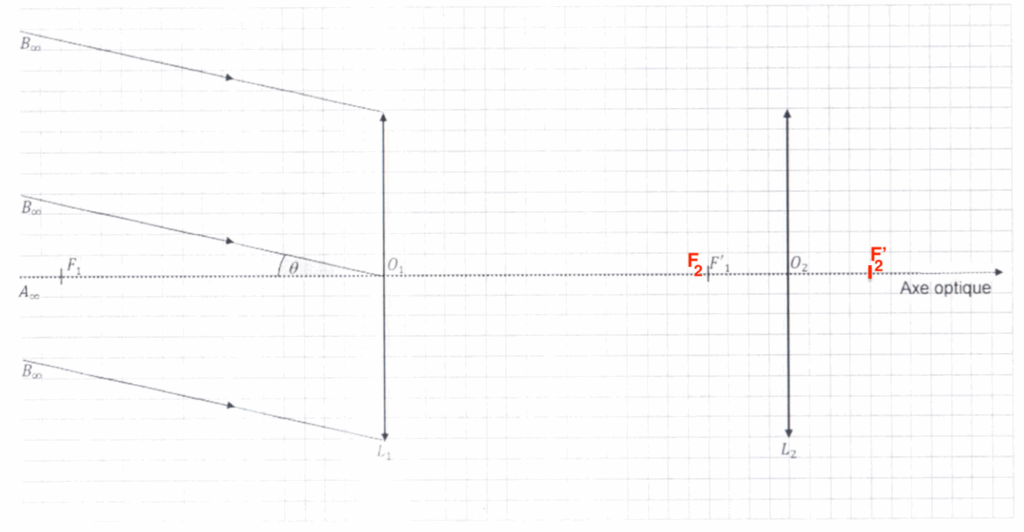
4. Indiquer comment le rayon lumineux issu de B∞ passant par le centre optique O1 traverse la lentille L1.
Le rayon lumineux issu de $B_\infty$ pénétrant dans la lunette par le centre optique $O_1$ de la lentille $L_1$ n’est pas dévié.
5. Sur le document réponse à rendre avec la copie, tracer le rayon lumineux issu de B∞ passant par le centre optique O1 de la lentille L1 permettant d’obtenir l’image intermédiaire A1B1.
Comme l’objet A∞B∞ est à l’infini, son image A1B1 est dans le plan focal image de l’objectif L1.
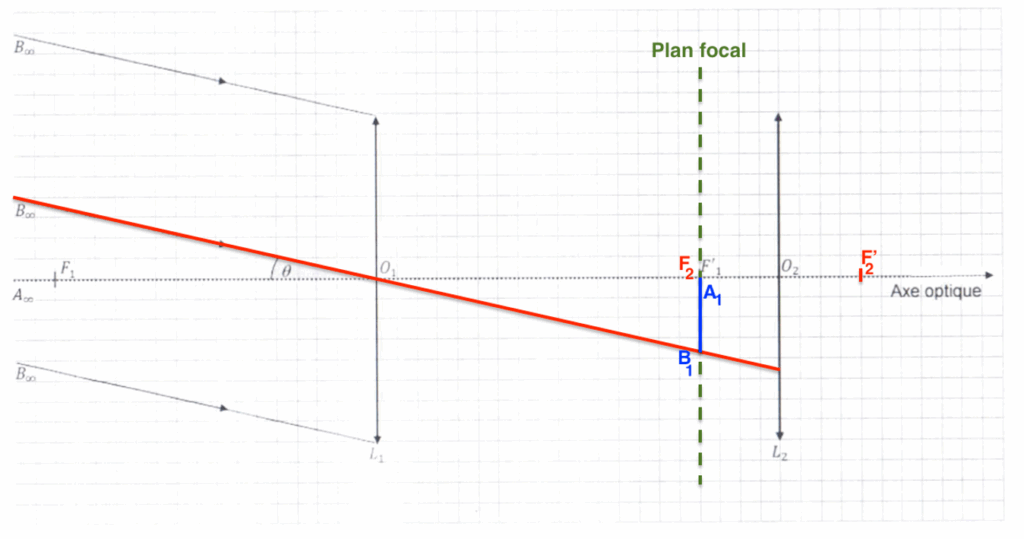
6. Donner les deux caractéristiques de l’image A1B1 obtenue.
L’image A1B1 est réelle et renversée.
7. Sur le document réponse à rendre avec la copie, tracer le rayon lumineux issu de B1 passant par le centre optique O2 de la lentille L2. On obtient alors l’image finale A2B2 de la Lune.
Pour le rayon émergeant de la lentille L2 :
On trace un rayon issu de B1 passant par O2. Ce rayon ne sera pas dévié.
De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi le rayon émergeant de la lentille L2 issue de B1 sera parallèle à ce rayon tracé.
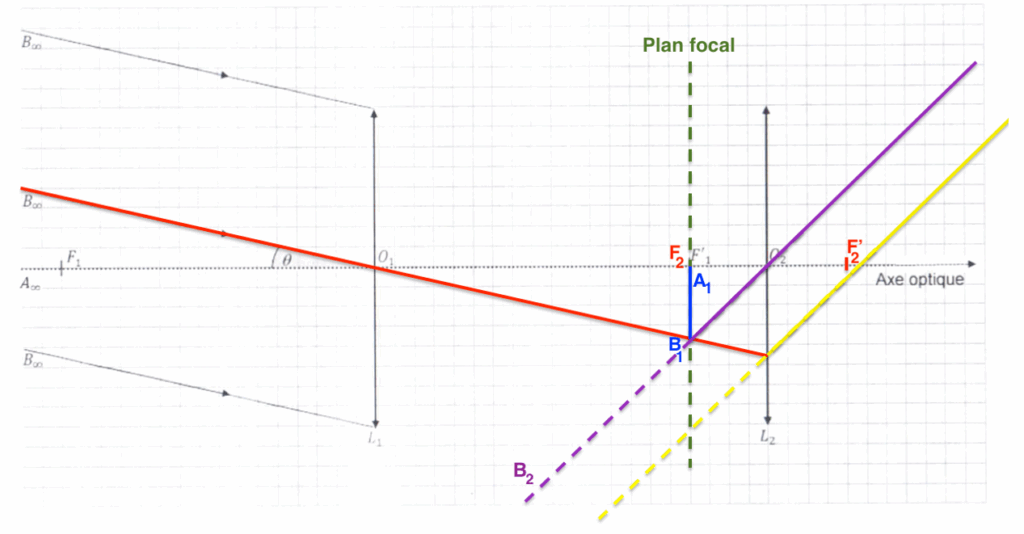
8. Sur le document réponse à rendre avec la copie, représenter le faisceau de rayons lumineux issu de l’objet B∞ passant par les bords de la lentille Lc puis la lentille L2.
Les rayons lumineux s’appuyant sur les bords de la lentille L1 sont issus de B. Ainsi, ils seront déviés vers B1.
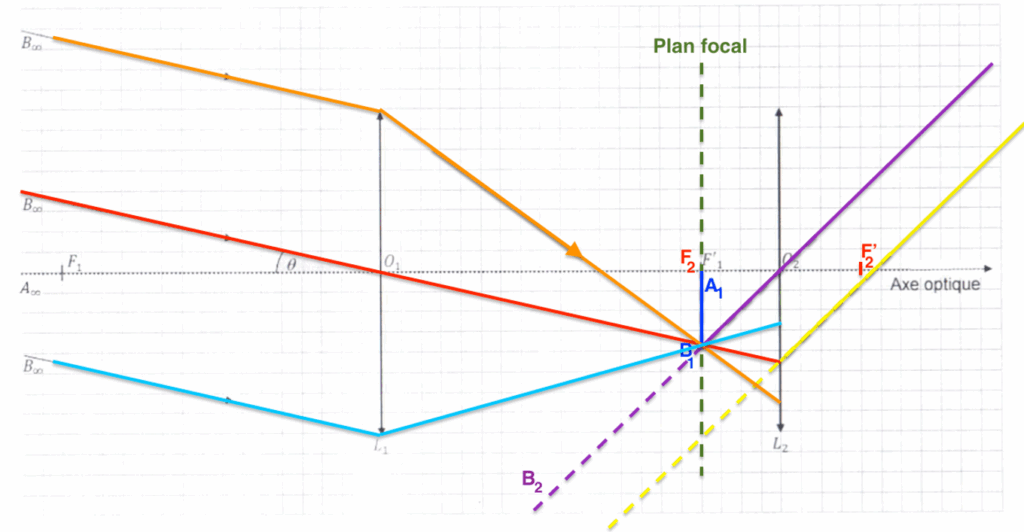
Pour leur sortie de la lunette par L2, les rayons seront parallèles aux autres rayons déjà tracés issus de B1 passant par la lentille L2.
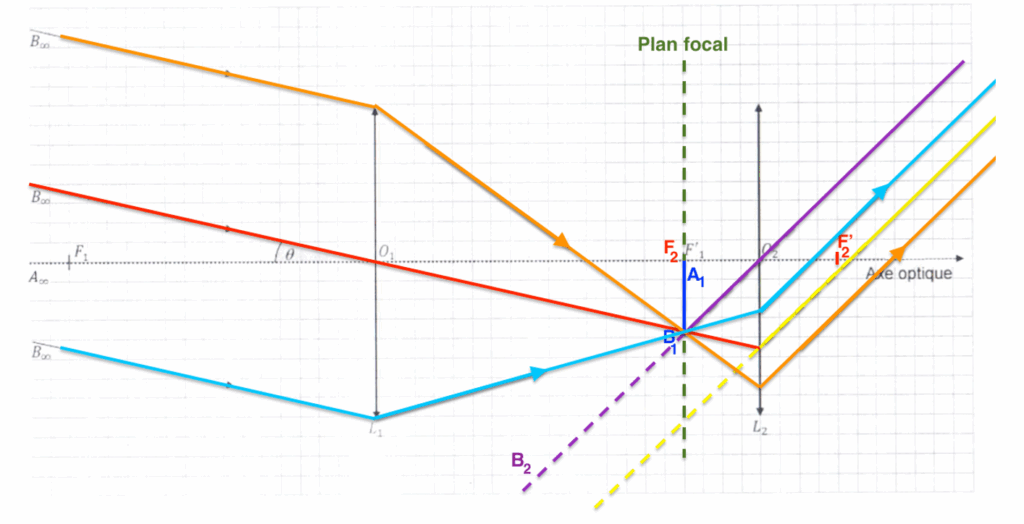
Grossissement de la lunette astronomique.
La Lune représentée par l’objet A∞B∞ est vue à l’œil nu sous l’angle θ, appelé diamètre apparent de la Lune.
9. Sur le document réponse à rendre avec la copie, positionner l’angle θ’ sous lequel est observée l’image finale de la Lune au travers de la lunette utilisée.
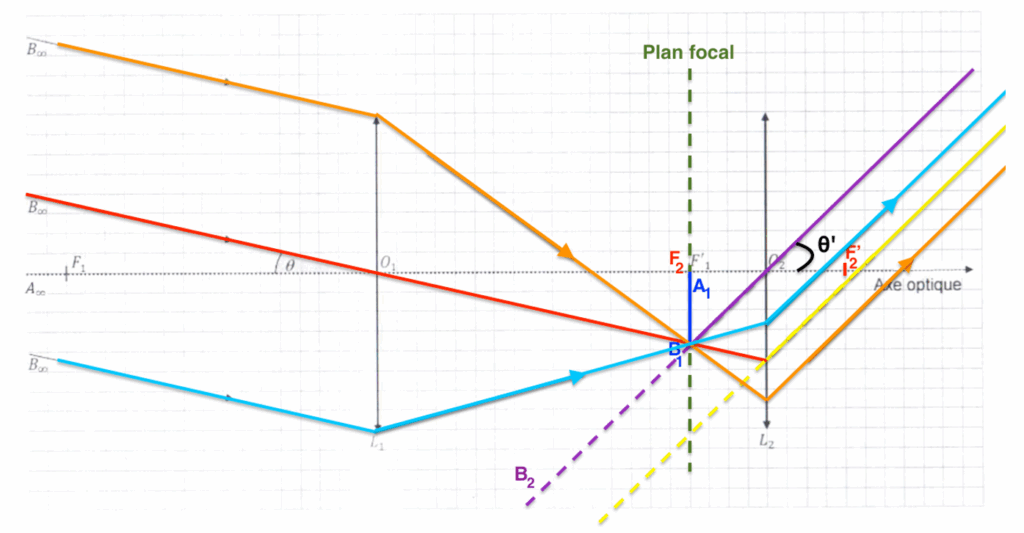
Le grossissement G de la lunette a pour expression : $G= \frac{\theta_1′}{\theta_2′} $ . Puisque les angles θ etθ’ sont petits, on acceptera, pour ces angles exprimés en radian, les approximations suivantes : tan θ = θ et tan θ’ = θ’.
10. Démontrer que le grossissement G s’exprime, également, par la relation $G= \frac{f_1′}{f_2′} $ où f1‘ représente la distance focale de l’objectif et f2‘ représente la distance focale de l’oculaire
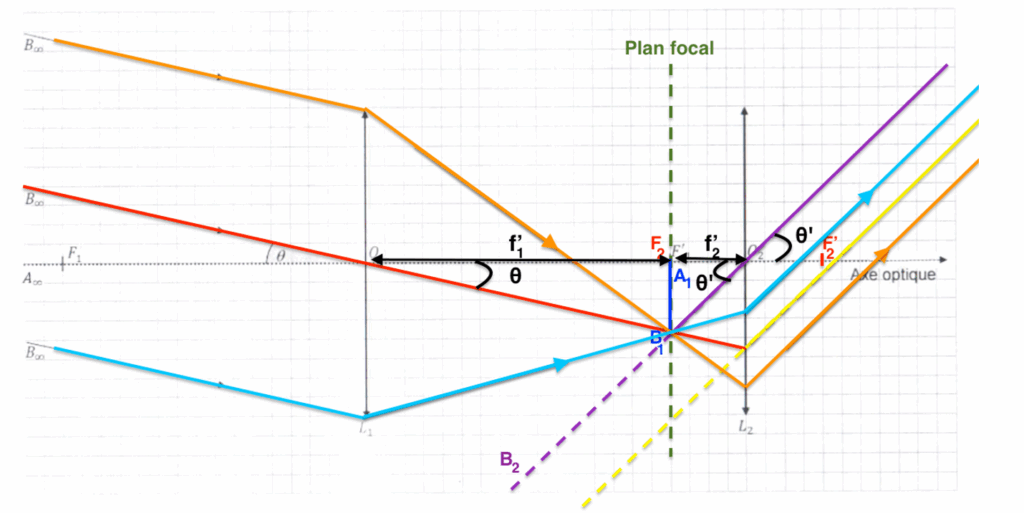
$$\tan\left(\theta\right)\approx\theta=\frac{A_1B_1}{f_1^\prime}$$
$$\tan\left(\theta^\prime\right)\approx\theta^\prime=\frac{A_1B_1}{f_2^\prime}$$
$$G=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times\frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$$
11. Calculer la valeur du grossissement G pour la lunette utilisée.
$$G=\frac{f_1^\prime}{f_2^\prime}$$
$$G=\frac{66{.10}^{-2}}{9,0{.10}^{-3}}$$
$$G=73$$
12. Comparer la valeur de G obtenue avec celle du fabriquant.
Le grossissement obtenu et celui indiqué par le fabriquant sont identiques.
L’observation de l’éclipse solaire du 10 juin 2021 peut se résumer simplement par le schéma ci-contre avec :
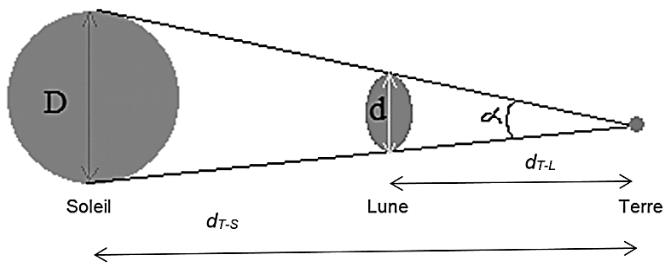
D : diamètre du soleil : 1,39×106 km
d : diamètre de la lune à déterminer
dT-L : distance Terre-Lune : 3,84×105 km
dT-S : distance Terre-Soleil : 1,50×108 km
α : diamètre apparent sous lequel un observateur voit la Lune et le Soleil lors de l’éclipse
Aux environs de midi ce jeudi 10 juin 2021, en levant les yeux au ciel, il sera possible d’observer – avec une protection adéquate – le disque du Soleil se faire recouvrir partiellement par la Lune. Ce phénomène appelé éclipse solaire a lieu lorsque la Lune se place entre le Soleil et la Terre, et que les trois sont alignés.
« … »
Dans le cas d’une éclipse totale, la Lune ayant un diamètre 400 fois plus petit que celui du Soleil, mais étant aussi 400 fois plus proche de la Terre, leurs deux diamètres coïncident et le recouvrement sera presque parfait. Mais ce type d’éclipse ne se produit que très rarement, car l’alignement entre le Soleil, la Lune et la Terre doit être parfait. Jeudi 10 juin, c’est une éclipse partielle de Soleil qui aura lieu. Ce phénomène se produit lorsque la Lune ne recouvre pas entièrement le Soleil, soit parce que son diamètre apparent est inférieur à celui du Soleil – on parle alors d’éclipse annulaire -, soit lorsque l’alignement n’est pas complètement parfait.
Extrait de la revue « Sciences et Avenir » du 7 juin 2021
Dans la question suivante, le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
13. Montrer que l’exploitation des données de l’éclipse solaire du 10 juin 2021 puis de l’extrait de la revue « Sciences et Avenir » du 7 juin 2021, pour déterminer le diamètre de la Lune, donne des valeurs similaires.
Déterminons le diamètre de la lune à l’aide des données de l’éclipse solaire du 10 juin 2021 :
D’après le théorème de Thales :
$$\frac{d}{D}=\frac{d_{T-L}}{d_{T-S}}$$
$$d=\frac{d_{T-L}}{d_{T-S}}\times D$$
$$d=\frac{3,84{.10}^5}{1,50{.10}^8}\times 1,39{.10}^6$$
$$d=3,56{.10}^3\ Km$$
Déterminons le diamètre de la lune à partir de l’extrait de la revue « Sciences et Avenir » du 7 juin 2021 :
$$d=\frac{D}{400}$$
$$d=\frac{1,39{.10}^6}{400}$$
$$d=3,48{.10}^3\ Km$$
Les deux valeurs trouvées sont similaires.
DOCUMENT RÉPONSE À RENDRE AVEC LA COPIE
EXERCICE B – ÉCLIPSE SOLAIRE DU 10 JUIN 2021
La figure a été réalisée sans soucis d’échelle.
Questions 3., 5., 7., 8. et 9. :