Enseignement scientifique première partie mathématique
Durée 0h48 – 12 points
Télécharger l’exercice en PDF :
Les parties A, B et D de cet exercice peuvent être traitées de façon indépendante.
Dans la partie C, on attend du candidat qu’il compare la pertinence des modèles étudiés dans les parties A et B.
Partie A
On injecte une dose de 1 gramme d’un médicament dans le sang d’un patient. On souhaite étudier la quantité de médicament présente dans le sang en fonction du temps. On sait que le médicament est progressivement éliminé par l’organisme de sorte que, chaque heure, la quantité de médicament présente dans le sang diminue de 30 %.
On modélise cette situation en notant, pour tout entier naturel 𝑛, 𝑢𝑛 la quantité de médicament (exprimée en grammes) qui est présente dans le sang du patient après 𝑛 heures écoulées depuis l’injection. Sous ces conditions, on a 𝑢0 = 1.
1- Justifier que, selon cette modélisation, 𝑢1 = 0,7 et 𝑢2 = 0,49 .
On admet alors que la suite (𝑢𝑛) est une suite géométrique de raison 0,7.
2- En déduire, pour tout entier naturel 𝑛, 𝑢𝑛 en fonction de 𝑛.
3- On sait que le médicament n’est plus actif lorsque la quantité présente dans le sang est strictement inférieure à 0,2 g. D’après cette modélisation, pendant quelle durée le médicament est-il actif ? Expliquer brièvement la démarche.
Partie B
Dans cette partie on suppose que la quantité de médicament présente dans le sang du patient (exprimée en grammes) peut être modélisée par la fonction 𝑓 définie sur l’intervalle [0 ; 12] par 𝑓(𝑡) = 0,7𝑡 où 𝑡 représente le temps écoulé depuis l’injection (exprimé en heures).
Ci-après, on donne la courbe représentative 𝐶𝑓 de la fonction 𝑓 dans un repère orthogonal du plan.
On a tracé en pointillés la droite tangente à 𝐶𝑓 au point A d’abscisse 3.
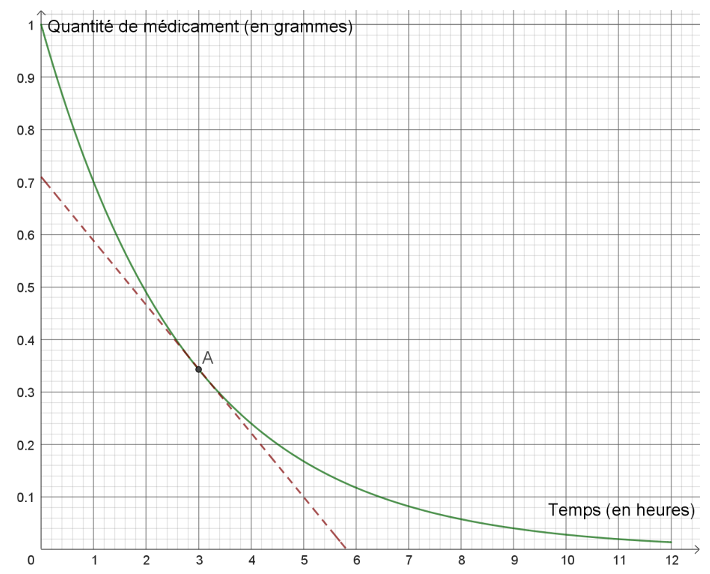
4- Avec la précision permise par le graphique, répondre aux deux questions suivantes :
4-a- Quelle est la quantité de médicament présente dans le sang trois heures après l’injection ?
4-b- Quelle est la valeur de 𝑓’(3)? Comment interpréter cette valeur dans le contexte de l’exercice ?
5-a- Recopier et compléter le tableau de valeurs ci-dessous à l’aide d’une calculatrice (on arrondira à 0,01).
| 𝑡 | 4 | 4,1 | 4,2 | 4,3 | 4,4 | 4,5 | 4,6 | 4,7 | 4,8 | 4,9 |
| 𝑓(𝑡) | 0,24 |
5-b- On rappelle que le médicament n’est plus actif lorsque la quantité présente dans le sang est strictement inférieure à 0,2 g.
Donner une valeur approchée à 0,1 du temps au bout duquel le médicament cesse d’être actif.
Partie C
On souhaite donner une indication précise sur la durée du principe actif du médicament.
6- D’après vous quel est le modèle le plus pertinent ? Justifier brièvement la réponse.
Partie D
Le médicament a pour but de faire baisser le taux de glycémie chez des patients ayant un taux de glycémie anormalement élevé. Afin de tester l’efficacité de ce médicament sur un groupe de patients (que l’on appellera « groupe-test » par la suite), on procède comme ceci : 60 % des patients de ce groupe reçoivent le médicament et les autres patients reçoivent un placebo.
À l’issue du traitement, on mesure leur taux de glycémie et les résultats sont les suivants :
- chez les patients ayant reçu le médicament, on observe une baisse du taux de glycémie dans 15 % des cas ;
- chez les patients ayant reçu le placebo, on n’observe aucune baisse du taux de glycémie dans 90 % des cas.
On choisit au hasard un patient du groupe-test et on note :
𝑀 l’événement « le patient a reçu le médicament »
$\overline{M}$ l’événement « le patient a reçu le placebo»
𝐵 l’événement « on observe chez le patient une baisse du taux de glycémie »
7- D’après les données ci-dessus, quelle est la valeur de 𝑃𝑀̅( 𝐵) ?
8- Calculer la probabilité 𝑃( $\overline{M}$ ∩ 𝐵) et interpréter ce résultat.
9- On admet que 𝑃(𝐵) = 0,13. On choisit au hasard un patient du groupe-test et on constate que son taux de glycémie a baissé. Quelle est la probabilité qu’il ait pris le placebo (on arrondira au centième) ?
10- À votre avis, peut-on considérer que ce test a prouvé l’efficacité du médicament ? Justifier.
