Émilie du Châtelet, Madame Pompon Newton

Bac Polynésie septembre 2024 Sujet 2

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ2PO3

Sujet et corrigé

EXERCICE 3 – ÉMILIE DU CHÂTELET, MADAME POMPON NEWTON (5 POINTS)

Madame Pompon Newton est le surnom donné à Émilie du Châtelet par Voltaire, son ami proche, en référence à sa coquetterie et à sa passion pour le travail de Newton. En effet, en utilisant un nouveau formalisme mathématique, elle traduit et commente l’œuvre de Newton Philosophiæ naturalis principia mathematica et ainsi permet la diffusion de la pensée de Newton dans toute l’Europe alors qu’elle est encore très peu connue à l’époque.

Voltaire écrit en préface : « cette traduction que les plus savants Hommes de France devaient faire et que les autres doivent étudier, une femme l’a entreprise et achevée à l’étonnement et à la gloire de son pays. […] On a vu deux prodiges : l’un, que Newton ait fait cet ouvrage ; l’autre, que Dame [Émilie du Châtelet] l’ait traduit et l’ait éclairci. »

L’objectif de cet exercice est d’étudier les trois lois de Newton en s’appuyant sur des extraits de cette traduction.

« Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état »

Figure 1. Extrait de Émilie du Châtelet, Principes mathématiques de la philosophie naturelle tome second, France, Édition Desaint, Saillant et Lambert, 1759.

Q1. Énoncer dans un langage plus actuel que celui de la figure 1 la première loi de Newton, aussi appelée principe d’inertie, ou donner les relations mathématiques qui la traduisent.

Dans un référentiel galiléen, le vecteur vitesse d’un système est constant si la somme vectorielle des forces qui s’exercent sur le système vaut le vecteur nul.

Relations mathématiques qui traduisent la première loi de Newton :
Si $\Sigma\vec{F_{ext}}=\vec{0}$ : $\vec{v}=\vec{constante}$

Un expérimentateur lâche dans l’air une plume et une boule de bowling d’une certaine hauteur. Dans l’air, la plume arrive en bas après la boule de bowling. La plume utilisée est photographiée figure 2.

Figure 2. Photographie de la plume.

Q2. Choisir, parmi les points A, B ou C de la figure 2, celui qui représente le centre de masse G de la plume.

Le point B de la figure 2 est celui qui représente le centre de masse G de la plume.

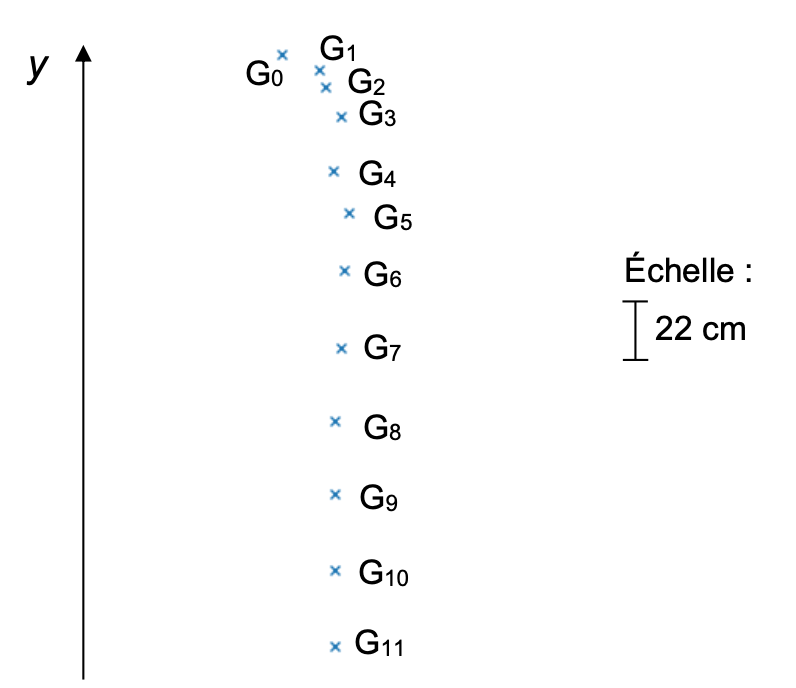
Figure 3. Chronophotographie du centre de masse G de la plume pour une chute dans l’air.

Dans la figure 3, l’intervalle de temps τ entre chaque point a une valeur égale à 0,085 s.

Q3. À l’aide la figure 3, calculer v₇ et v₉, les valeurs des vitesses aux points G₇ et G₉.

Deux formules pour calculer la vitesse instantanée :
Formule 1 :
$$v_i=\frac{G_iG_{i+1}}{\tau}$$
Formule 2 :
$$v_i=\frac{G_{i-1}G_{i+1}}{2\tau}$$

Avec la formule 1 :
$$v_7=\frac{G_7G_8}{\tau}$$

Schéma	Réel
0,7 cm	22 cm
0,95 cm	G7G8

$$G_7G_8=\frac{0,95\times22}{0,7}$$
$$G_7G_8=30\ cm$$

$$v_7=\frac{30\times{10}^{-2}}{0,085}$$
$$v_7=3,5\ m\cdot s^{-1}$$

$$v_9=\frac{G_9G_{10}}{\tau}$$

Schéma	Réel
0,7 cm	22 cm
0,95 cm	G9G10

$$G_9G_{10}=\frac{0,95\times22}{0,7}$$
$$G_9G_{10}=30\ cm$$

$$v_9=\frac{30\times{10}^{-2}}{0,085}$$
$$v_9=3,5\ m\cdot s^{-1}$$

Avec la formule 2 :
$$v_7=\frac{G_6G_8}{2\tau}$$

Schéma	Réel
0,7 cm	22 cm
1,9 cm	G6G8

$$G_6G_8=\frac{1,9\times22}{0,7}$$
$$G_6G_8=60\ cm$$

$$v_7=\frac{60\times{10}^{-2}}{2\times0,085}$$
$$v_7=3,5\ m\cdot s^{-1}$$

$$v_9=\frac{G_8G_{10}}{2\tau}$$

Schéma	Réel
0,7 cm	22 cm
1,9 cm	G8G10

$$G_8G_{10}=\frac{1,9\times22}{0,7}$$
$$G_8G_{10}=60\ cm$$

$$v_9=\frac{60\times{10}^{-2}}{2\times0,085}$$
$$v_9=3,5\ m\cdot s^{-1}$$

Dans la suite de l’exercice nous approximerons la portion du mouvement entre les points G₆ et G₁₁ comme étant rectiligne uniforme. De plus, nous considérerons comme négligeable l’effet de la poussée d’Archimède, exercée par l’air sur la plume, devant les autres forces.

Données :

• L’intensité de la pesanteur terrestre g a une valeur égale à 9,81 N·kg^–1 ;
• La masse m de la plume a une valeur égale à 0,985 g.

Q4. Dresser la liste des forces qui s’appliquent à la plume lors de sa chute dans l’air. Puis donner, dans la portion du mouvement entre les points G₆ et G₁₁, en justifiant, la relation mathématique qui les lie. À l’aide des données, déduire par un calcul la valeur f de la force de frottement.

Liste des forces qui s’appliquent à la plume lors de sa chute dans l’air :
Le poids $\vec{P}$
Les forces de frottements $\vec{f}$

D’après le sujet : « la portion du mouvement entre les points G6 et G11 comme étant rectiligne uniforme »
Le mouvement étant rectiligne uniforme, d’après la première loi de Newton :
$$\Sigma\vec{F_{ext}}=\vec{0}$$
$$\vec{P}+\vec{f}=\vec{0}$$
$$\vec{f}=-\vec{P}$$

Remarque : le signe moins indique que les forces ont des sens opposés.

D’où
$$f=P$$

Or
$$P=m\times g$$

D’ou
$$f=m\times g$$
$$f=0,985\times{10}^{-3}\times9,81$$
$$f=9,66\times{10}^{-3}\ N$$

Voici ce qu’écrit Émilie du Châtelet à propos de la deuxième loi du mouvement :

« Que le changement qui arrive dans le mouvement est toujours proportionnel à la force motrice, et se fait dans la direction de cette force. »

Figure 4. Extrait issu de Principes mathématiques de la philosophie naturelle d’Émilie du Châtelet.

Q5. Énoncer dans un langage plus actuel la deuxième loi de Newton ou donner la relation mathématique qui la traduit.

Deuxième loi de newton : Dans un référentiel galiléen, la somme vectorielle des forces extérieures qui s’exercent sur le solide est égale au produit de la masse et de l’accélération :
$$\Sigma\vec{F_{ext}}=m\vec{a}$$

La même expérience que précédemment a été réalisée mais cette fois la plume et la boule de bowling sont lâchées dans une chambre à vide, c’est-à-dire dans un espace hermétique où l’expérimentateur a retiré la quasi-totalité de l’air. L’influence des frottements peut alors être négligée.

D’une hauteur H, dans le vide, un dispositif permet de lâcher sans vitesse initiale et simultanément la boule de bowling et la plume. Ces deux objets frappent le sol exactement en même temps.

Dans la suite de l’exercice, on prendra l’origine des axes (Ox) et (Oy) au sol. L’axe (Oy) est dirigé vers le haut.

Q6. À l’aide de la deuxième loi de Newton, dans les conditions de la deuxième expérience, établir l’expression de l’altitude y(t) d’un système en chute libre et montrer qu’elle est indépendante de sa masse m.

Système {balle de bowling ou plume}
Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :
$$\Sigma\vec{F_{ext}}=m\vec{a}$$
$$\vec{P}=m\vec{a}$$
$$m\vec{g}=m\vec{a}$$
$$\vec{g}=\vec{a}$$

Or
$$\vec{g}\ \left|\begin{matrix}0\\-g\end{matrix}\right.$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\vec{a}\ \left|\begin{matrix}a_x=0\\a_y=-g \end{matrix}\right.$$

Ainsi : $a_{y\left(t\right)}=-g$

$$a_y=\frac{dv_{y\left(t\right)}}{dt}$$
On intègre l’accélération :
$${v}{y\left(t\right)}=-gt+C_1$$
Pour trouver les constantes, on utilise la vitesse initiale. Or, d’après le sujet, un dispositif permet de lâcher sans vitesse initiale et simultanément la boule de bowling et la plume : $v{0y}=0$
d’ou
$${v}{y\left(t\right)}=-gt$$
$${v}{y\left(t\right)}=\frac{dy\left(t\right)}{dt}$$
On intègre la vitesse :
$$y\left(t\right)=-\frac{1}{2}gt^2+C_2$$
Pour trouver les constantes, on utilise $z_0=H$
D’ou
$$y\left(t\right)=-\frac{1}{2}gt^2+H$$

Ainsi, l’altitude $y(t)$ d’un système en chute libre est indépendante de sa masse $m$.

L’évolution de l’accélération, de la vitesse et de la position suivant l’axe vertical ont été représentées sur la figure 5.

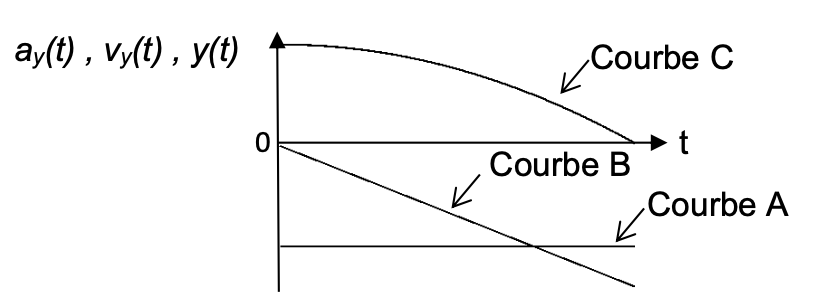
Figure 5. Courbes A, B, et C.

Q7. Attribuer chaque courbe (A, B et C) de la figure 5 à une coordonnée parmi les trois suivantes : a_y(t), v_y(t), y(t).

$a_{y\left(t\right)}=-g$ : l’accélération est constante, elle ne dépend pas du temps. Courbe A
$v_{y\left(t\right)}=-gt$ : la vitesse est une fonction linéaire décroissante : c’est une droite passant par l’origine. Courbe B
$y\left(t\right)=-\frac{1}{2}gt^2+H$ : l’altitude est une fonction du second degré : c’est une parabole. Courbe C

Q8. La valeur de la vitesse vd de l’objet est égale à 14 m·s^–1 quand l’objet arrive à une distance d = 20 cm au-dessus du sol. En déduire la valeur de la hauteur H depuis laquelle les objets sont lâchés.

La valeur de la vitesse $v_d$ de l’objet est égale à 14 m·s–1 quand l’objet arrive à une distance $d = 20$ cm au-dessus du sol.
On cherche $H$ :
$$y\left(t\right)=-\frac{1}{2}gt^2+H$$
$$-\frac{1}{2}gt^2+H=y\left(t\right)$$
$$H=y\left(t\right)+\frac{1}{2}gt^2$$

Il faut trouver $t$ :
$$v_{y\left(t\right)}=-gt$$
$$-gt=v_{y\left(t\right)}$$
$$t=\frac{v_{y\left(t\right)}}{-g}$$

En remplacant $t$ dans la relation précedente on obtient :
$$H=y\left(t\right)+\frac{1}{2}g\left(\frac{v_{y\left(t\right)}}{-g}\right)^2$$
$$H=y\left(t\right)+\frac{1}{2}g\times\frac{{v_{y\left(t\right)}}^2}{g^2}$$
$$H=y\left(t\right)+\frac{1}{2}\times\frac{{v_{y\left(t\right)}}^2}{g}$$
$$H=20\times{10}^{-2}+\frac{1}{2}\times\frac{{14}^2}{9,81}$$
$$H=10\ m$$

Extrait n°1. Lorsque les corps sont jetés en haut, la gravité leur imprime des forces et leur ôte des vitesses proportionnelles au temps.

Extrait n°2. Si un cheval tire une pierre par le moyen d’une corde, il est également tiré par la pierre : car la corde qui les joint et qui est tendue des deux côtés, fait un effort égal pour tirer la pierre vers le cheval et le cheval vers la pierre ; et cet effort s’oppose autant au mouvement de l’un, qu’il excite le mouvement de l’autre.

Extrait n°3. Les projectiles par eux-mêmes persévèrent dans leurs mouvements, mais la résistance de l’air les retarde et la force de gravité les porte vers la Terre.

Figure 6. Extraits issus de Principes mathématiques de la philosophie naturelle d’Émilie du Châtelet.

Q9. La figure 6 présente trois extraits qui servent à illustrer, chacun, une loi de Newton. Choisir parmi ces trois extraits celui qui illustre la troisième loi de Newton en précisant la ou les raisons de votre choix.

Troisième loi de Newton : Tout corps A exerçant une force sur un corps B subit une force d’intensité égale, de même direction mais de sens opposé, exercée par le corps B.
$$\overrightarrow{F_{A/B}}=-\overrightarrow{F_{B/A}}$$
L’extrait qui illustre la troisième loi de Newton est l’extrait n°2 « Si un cheval tire une pierre par le moyen d’une corde, il est également tiré par la pierre : car la corde qui les joint et qui est tendue des deux côtés, fait un effort égal pour tirer la pierre vers le cheval et le cheval vers la pierre ; et cet effort s’oppose autant au mouvement de l’un, qu’il excite le mouvement de l’autre. »