Enseignement scientifique première
Durée 1h – 10 points – Thème « Son et musique, porteurs d’information »
[latexpage]
On s’interroge sur la pertinence d’utiliser un smartphone pour télécharger et stocker de la musique. Pour cela, on étudie le lien entre la qualité de la numérisation d’un signal audio et la taille des fichiers numériques correspondants.
Partie A : échantillonnage et quantification d’un signal audio
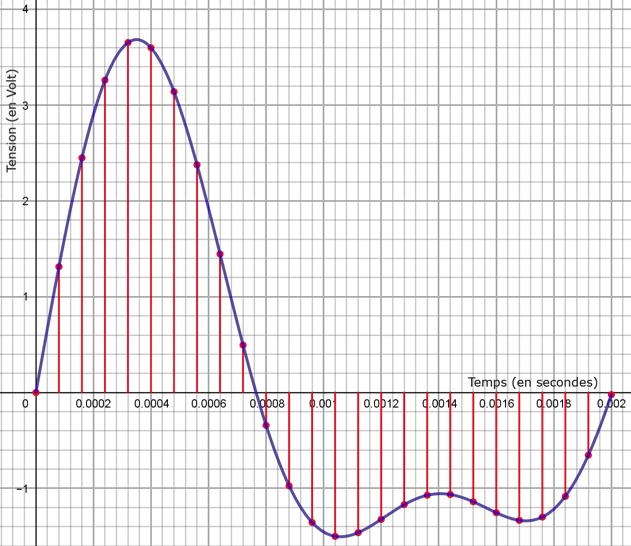
Le document 1 donné en annexe et à rendre avec la copie représente une portion de signal enregistré et l’échantillonnage effectué avant la conversion en signal numérique.
1- Préciser la fréquence d’échantillonnage, choisie parmi les valeurs proposées ci- dessous :
2 000 Hz ; 12 500 Hz ; 26 000 Hz ; 44 100 Hz
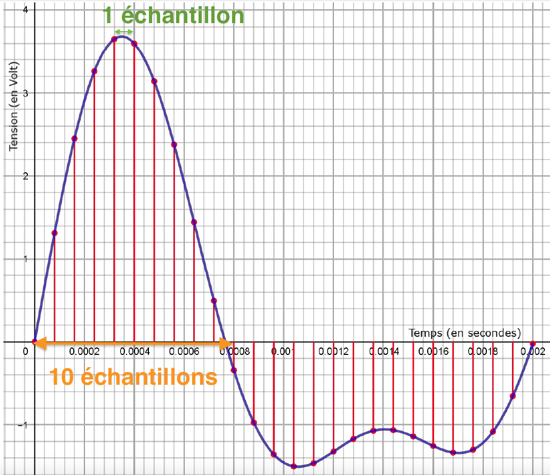
| 10 échantillons | 0,0008 |
| 1 échantillon | 0,00008 |
f=1/T
f=1/0,00008
f=12 500 hz
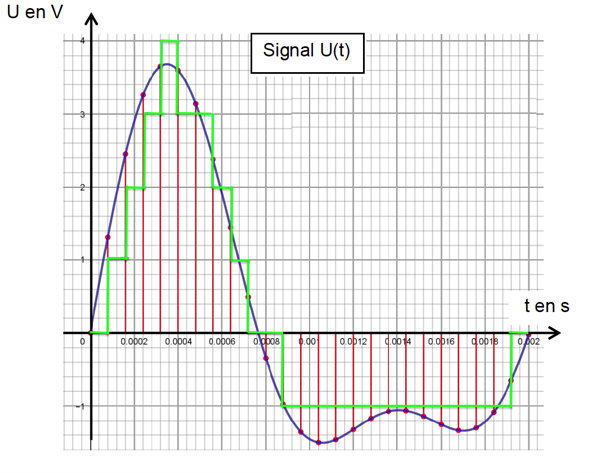
2- Après l’échantillonnage du signal audio, on procède à sa quantification. On admet que la tension quantifiée ne prend que des valeurs entières ; la valeur quantifiée d’une tension est l’entier le plus proche de cette tension.
Sur le document 1 en annexe, à rendre avec la copie, représenter la courbe des tensions après quantification.
3- Une plateforme de service de musique en ligne propose de la musique en qualité « 16-Bits / 44.1 kHz ».
Expliquer ce que représentent ces deux valeurs.
16-Bits : quantification qui nous renseigne sur le nombre de valeurs pouvant être prise.
44.1 kHz : fréquence d’échantillonnage qui est le nombre de prélèvements effectués par seconde.
4- Combien de niveaux de quantification différents peut-on obtenir lorsque le codage s’effectue sur 16 bits ? Choisir la bonne réponse parmi les propositions suivantes :
16 2 × 16 = 32 162 = 256 216 = 65 536
216 = 65 536
Partie B : taille d’un fichier en haute définition
Dans un studio d’enregistrement, on enregistre un morceau de musique en stéréo haute définition en choisissant un encodage sur 24 bits et une fréquence d’échantillonnage de 192 kHz.
5- La taille T(en bit) d’un fichier audio numérique s’exprime en fonction de la fréquence d’échantillonnage 𝑓𝑒 (en Hertz), du nombre 𝑛 de bits utilisés pour la quantification, de la durée Δ𝑡 de l’enregistrement et du nombre 𝑘 de voies d’enregistrement (une en mono, deux en stéréo) selon la relation :
T =fe×n×Δt×k
Vérifier que l’espace de stockage nécessaire pour enregistrer en stéréo haute définition une seconde de musique est de 1,152 Mo. On rappelle qu’un octet est égal à 8 bits.
T =fe×n×Δt×k
T =192.103×24×1×2
T =9,216.106 bits
T =(9,216.106)/8
T =1,152.106 octets
T =1,152 Mo
6- Avec 200 Mo de stockage, dispose-t-on de suffisamment d’espace pour enregistrer cinq minutes de musique en stéréo haute définition ?
Méthode 1 :
| 1 seconde | 1,152 Mo |
| 5 min=5×60=300 secondes |
x=(300×1,152)/1
x=345,6 Mo
Avec 200 Mo de stockage on ne dispose pas de suffisamment d’espace pour enregistrer cinq minutes de musique en stéréo haute définition.
Méthode 2 :
T =fe×n×Δt×k
T =192.103×24×5×60×2
T =2,7648.109 bits
T =(2,7648.109)/8
T =3,456.108 octets
T =345,6 Mo
Avec 200 Mo de stockage on ne dispose pas de suffisamment d’espace pour enregistrer cinq minutes de musique en stéréo haute définition.
7- Le dispositif d’encodage et de compression FLAC (Free Lossless Audio Codec) permet, par compression sans perte, de réduire de 55 % la taille des fichiers. Son taux de compression, défini comme le rapport de la taille du fichier compressé sur la taille du fichier initial, est donc de 45%.
Avec 200 Mo de stockage, dispose-t-on de suffisamment d’espace pour enregistrer cinq minutes de musique en stéréo haute définition compressées par FLAC ?
45/100×345,6=155,52 Mo
Avec 200 Mo de stockage on dispose de suffisamment d’espace pour enregistrer cinq minutes de musique en stéréo haute définition compressées par FLAC.
Document réponse à rendre avec la copie
Enregistrement de fichiers sonores
Document 1 – Question 2
Représentation de la tension d’un signal audio analogique en fonction du temps et mesures après échantillonnage.