Bac Polynésie 2024 Sujet 2
Exercice 3 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°24-PYCJ2PO1
Sujet et corrigé
EXERCICE 3 – ÉTUDE DE LA CALÉFACTION (5 POINTS)
La caléfaction est le comportement particulier d’une goutte d’eau déposée sur une plaque très chaude : elle ne se volatilise pas ni immédiatement ni totalement mais demeure jusqu’à quelques minutes à l’état liquide au-dessus de la plaque, flottant sur un coussin de vapeur. Ce phénomène a été étudié pour la première fois en 1756 par Johann LEIDENFROST.
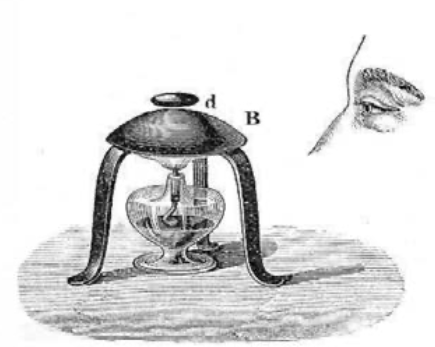
D’après « Heat: a mode of motion », J. Tyndall, (1875). p. 158
Figure 1. Observation de l’espace entre la base chauffée B, et une goutte d.
L’objectif de cet exercice est de déterminer la valeur de la distance entre la goutte et la plaque.
On appelle durée de vie, la durée au bout de laquelle la goutte s’est complétement évaporée après son dépôt. Cette durée est étudiée expérimentalement en fonction de la température de la plaque sur laquelle est déposée une goutte de volume 50 µL à 20 °C. Les résultats sont reportés dans le graphique ci-dessous : pour différentes températures, on note la durée de vie et sa barre d’incertitude.
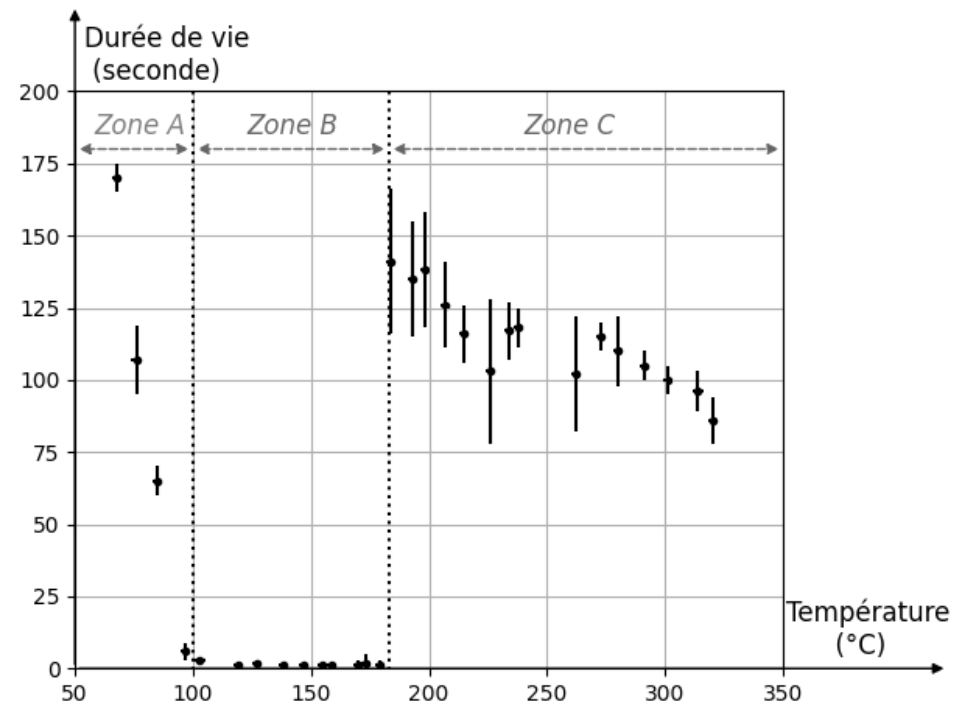
D’après « la caléfaction froide », Olympiades de physique 2015.
Figure 2. Durée de vie d’une goutte de 50 µL en fonction de la température de la plaque.
Dans le cadre de cet exercice, la zone A présentée sur la figure 2 ne présente pas d’intérêt car la température associée aux valeurs de durées de vie est inférieure à la température d’ébullition de l’eau. En revanche, au-delà de cette température (100 °C), on distingue deux zones pour lesquelles le comportement de la goutte est différent.
Q1. À l’aide de la figure 2, proposer un argument afin de justifier le manque d’intérêt de la zone B pour l’étude de la caléfaction.
Le but est de déterminer la distance entre la goutte et la plaque lors de la caléfaction. Et pour ce faire, il faut que la durée de vie soit assez longue pour pouvoir étudier et observer. Or dans la zone B (figure 2), les durées de vie sont tellement rapides, par conséquent il est très difficile d’étudier la caléfaction dans cette zone. Donc la zone B ne porte pas d’intérêt pour l’étude.
John Tyndall a montré en 1875 que dans la zone C, au-delà de 180°C, appelé seuil de Leidenfrost, la goutte peut persister quelques minutes avant de se vaporiser. Pour mesurer l’épaisseur du coussin de vapeur sur lequel flotte la goutte on fait passer un faisceau lumineux entre la goutte et la plaque.
Lorsqu’on envoie un faisceau laser de longueur d’onde λ, on observe sur un écran placé à une distance D = 2,00 m le phénomène représenté figure 4. On note a l’épaisseur du coussin de vapeur entre la goutte et la plaque chauffée.
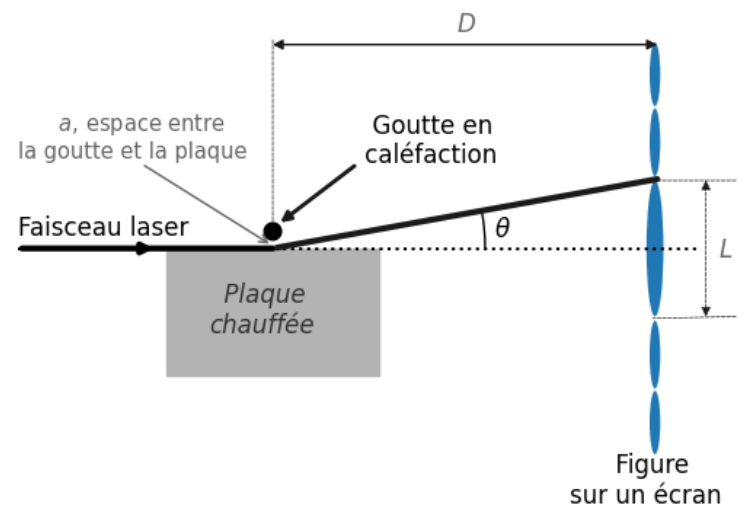
Figure 3. Schéma de la situation.
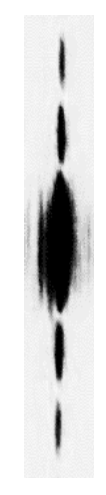
Figure 4. Photographie de l’écran.
Q2. Nommer le phénomène observé sur la figure 4.
On a donc un phénomène de diffraction, et la figure 4 montre la figure de diffraction obtenue.
Q3. Donner une condition sur la taille de l’espace a, entre la goutte et la plaque, pour que ce phénomène soit facilement observable avec un laser de longueur d’onde λ.
La condition nécessaire pour avoir le phénomène de diffraction avec le laser et l’espace est qu’il faut avoir : $a<10\cdot \lambda$
Donnée :
- Pour un petit angle exprimé en radians, θ = tan θ.
Q4. Montrer à l’aide de la figure 3 que dans l’approximation des petits angles, on peut écrire que $\theta=\frac{L}{2\cdot D}$∙
D’après la formule de trigonométrie et la situation (figure 3) : $\tan\left(\theta\right)=\frac{\frac{L}{2}}{D}$
Donc : $\tan\left(\theta\right)=\frac{L}{2D}$ ; or d’après l’approximation des petits angles : $\tan\left(\theta\right)\approx\theta$
Ainsi : $\theta=\frac{L}{2D}$
Donnée :
- L’angle θ dépend de la longueur d’onde λ du laser et de l’espace a entre la goutte et la plaque : $\theta=\frac{\lambda}{a}$∙
Q5. Établir l’expression de a en fonction de D, L et θ.
On a : $\theta=\frac{L}{2D}$ et $\theta=\frac{\lambda}{a}$
Donc : $\frac{\lambda}{a}=\frac{L}{2D}$
Et : $a=\frac{\lambda\times2D}{L}$
Une lecture de la photographie de la figure 4 par un logiciel de traitement de l’image donne le résultat de la figure 5.
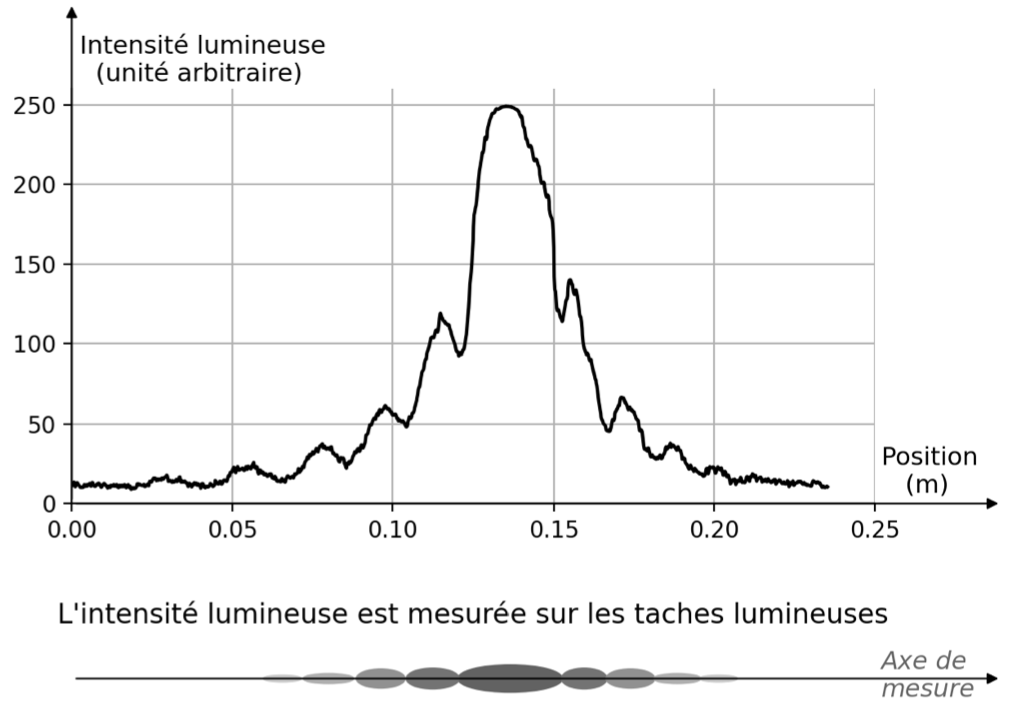
Figure 5. Résultat de l’analyse de la photographie obtenue.
Q6. En vous appuyant sur la figure 5, déterminer la valeur de la largeur de la tache centrale L.
Echelle : 2,5 cm à la règle graduée représente 0,05 m (donc 5 cm) dans la réalité.
La grande tâche primaire mesure 1,6 cm à la règle graduée, donc :
$L=\frac{1,6\times5}{2,5}=3,2\ cm=3,2\cdot{10}^{-2}\ m$. Donc, la grande tâche mesure 3,2 cm dans la réalité.
Donnée :
- La longueur d’onde λ du laser utilisé est de valeur égale à 532 nm.
Q7. Calculer la valeur de l’intervalle a entre la goutte et la plaque.
On utilise la formule : $a=\frac{\lambda\times2D}{L}$
A.N. : $a=\frac{532\times{10}^{-9}\times2\times2,00}{3,2\times{10}^{-2}}=6,65\cdot{10}^{-5}\approx67\cdot{10}^{-6}=67\ \mu m$.
Donc la distance entre la goutte et la plaque est de 67 µm environ.
