Étude d’une bouteille isotherme

Bac Métropole Septembre 2024 Sujet 1

Exercice 3 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°24-PYCJ1ME3

Exercice 3 – Étude d’une bouteille isotherme (6 points)

L’objectif de cet exercice est d’évaluer la capacité thermique du vase interne d’une bouteille isotherme, schématisée en figure 1, et d’en déduire la nature possible du métal qui constitue ce vase.

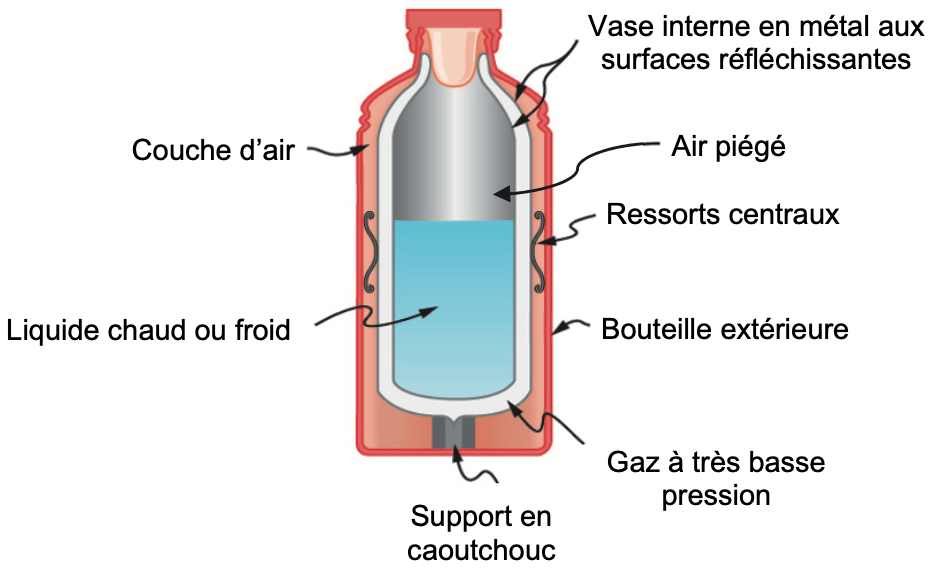
Figure 1. Schéma simplifié, en coupe, d’une bouteille isotherme

1. Constitution de la bouteille isotherme et échanges thermiques

Dans les bouteilles isothermes de qualité médiocre, l’espace entre le vase interne et la bouteille extérieure est rempli d’un matériau qui joue le rôle d’isolant thermique (polystyrène par exemple).

Dans le cas de la bouteille isotherme de qualité supérieure étudiée ici et représentée sur la figure 1, le vase interne n’est pas en contact direct avec la paroi de la bouteille extérieure et est maintenu par des ressorts centraux et un support en caoutchouc.

Q1. Identifier le mode de transfert thermique entre le vase interne et l’extérieur que l’usage des ressorts centraux et du support en caoutchouc vise à minimiser.

L’usage des ressorts centraux et du support en caoutchouc vise à minimiser le transfert thermique par conduction.

Q2. Expliquer l’intérêt de rendre réfléchissantes les surfaces intérieure et extérieure du vase interne.

Les surfaces intérieure et extérieure du vase interne sont réfléchissantes afin de supprimer le transfert thermique par rayonnement.

Q3. L’espace situé entre la surface intérieure et la surface extérieure du vase interne contient un gaz à très basse pression. Expliquer l’intérêt de ce choix.

Le gaz a très faible permet de réduire le transfert thermique par convection.

2. Expérience visant à déterminer la capacité thermique du vase interne de la bouteille isotherme

On verse une masse d’eau froide m_EF = 300 g dans la bouteille isotherme. Le vase interne et l’eau froide sont à la température initiale θ_EF = 15°C. On complète le contenu de la bouteille avec une masse d’eau chaude m_EC = 100 g à la température θ_EC = 60 °C. La bouteille isotherme pleine est rapidement fermée puis agitée légèrement. Après trois minutes, la température d’équilibre thermique est atteinte et vaut θ_éq = 26 °C.

Données :

• capacités thermiques massiques de plusieurs métaux à la pression atmosphérique et à la température de 25°C :

Matériau	Capacité thermique massique (J·kg−1·K−1)
Argent	235
Acier inoxydable	450
Titane	520
Aluminium	900

• on néglige l’influence de l’air piégé après fermeture de la bouteille isotherme ;
• la température de l’air extérieur et la pression atmosphérique sont constantes pendant la durée des expériences ;
• la température de l’air extérieur vaut : θ_ext = 19 °C ;la capacité thermique du vase interne de la bouteille isotherme est notée C_Vase ;la capacité thermique massique de l’eau est constante et vaut : c_E = 4,18×10³ J·kg⁻¹·K⁻¹ ;
• la durée de l’expérience est : Δt = 180 s.

On modélise la bouteille isotherme par un système {S} constitué des trois sous-systèmes :

• {Vase interne} ;
• {Eau froide introduite dans le vase} ;
• {Eau chaude introduite dans le vase}.

Les variations d’énergie interne de chacun des sous-systèmes s’écrivent :

• ΔU_Vase = C_Vase · (θ_éq – θ_EF) pour le sous-système {vase interne} ;
• ΔU_{Eau froide} = m_EF · c_E · (θ_éq – θ_EF) pour le sous-système {eau froide} ;
• ΔU_{Eau chaude} = m_EC · c_E · (θ_éq – θ_EC) pour le sous-système {eau chaude}.

Pendant l’expérience, on considère que le système {S} vérifie les hypothèses suivantes :

• hypothèse 1 : les transferts thermiques avec le milieu extérieur sont négligés ;
• hypothèse 2 : les transferts d’énergie sous forme de travail sont également négligés.

Au regard du modèle retenu, la variation d’énergie interne du système {S} s’écrit :

ΔU_S = ΔU_Vase + ΔU_{Eau froide} + ΔU_{Eau chaude}

Q4. Indiquer en quoi les deux hypothèses faites permettent d’écrire que le premier principe de la thermodynamique appliqué au système {S} donne : ΔU_S = 0.

Premier principe de la thermodynamique :
$\Delta U_S=Q+W$
Hypothèse 1 : les transferts thermiques avec le milieu extérieur sont négligés : $Q=0$
Hypothèse 2 : les transferts d’énergie sous forme de travail sont également négligés : $W=0$
$\Delta U_S=0+0$
$\Delta U_S=0$

Ainsi, les deux hypothèses faites permettent d’écrire que le premier principe de la thermodynamique appliqué au système {S} donne : $\Delta U_S = 0$.

Q5. En déduire que la capacité thermique C_Vase est donnée par la relation :

$$C_{vase}=\frac{m_{EC}\cdot c_E\cdot\left(\theta_{EC}-\theta_{eq}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}-m_{EF}\cdot c_E$$

$\Delta U_S=\Delta U_{Vase}+\Delta U_{Eau\ froide}+\Delta U_{Eau\ chaude}$
Or
$\Delta U_S=0$

D’où
$\Delta U_{Vase}+\Delta U_{Eau\ froide}+\Delta U_{Eau\ chaude}=0$

Or d’après les données
$\Delta U_{Vase}=C_{Vase}\cdot\left(\theta_{eq}-\theta_{EF}\right)$
$\Delta U_{Eau\ froide}=m_{EF}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EF}\right)$
$\Delta U_{Eau\ chaude}=m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)$

D’où
$C_{Vase}\cdot\left(\theta_{eq}-\theta_{EF}\right)+m_{EF}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EF}\right)+m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)=0$
$C_{Vase}\cdot\left(\theta_{eq}-\theta_{EF}\right)=-m_{EF}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EF}\right)-m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)$
$C_{Vase}=\frac{-m_{EF}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EF}\right)-m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$

$C_{Vase}=-\frac{m_{EF}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EF}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}-\frac{m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$
$C_{Vase}=-m_{EF}\cdot c_E+\frac{-m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$
$C_{Vase}=-m_{EF}\cdot c_E+\frac{m_{EC}\cdot c_E\cdot\left(-\theta_{eq}-\left(-\theta_{EC}\right)\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$
$C_{Vase}=-m_{EF}\cdot c_E+\frac{m_{EC}\cdot c_E\cdot\left(-\theta_{eq}+\theta_{EC}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$
$C_{Vase}=-m_{EF}\cdot c_E+\frac{m_{EC}\cdot c_E\cdot\left(\theta_{EC}-\theta_{eq}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}$
$C_{Vase}=\frac{m_{EC}\cdot c_E\cdot\left(\theta_{EC}-\theta_{eq}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}-m_{EF}\cdot c_E$

Q6. Calculer la valeur de la capacité thermique C_Vase.

$C_{Vase}=\frac{m_{EC}\cdot c_E\cdot\left(\theta_{EC}-\theta_{eq}\right)}{\left(\theta_{eq}-\theta_{EF}\right)}-m_{EF}\cdot c_E$
$C_{Vase}=\frac{100\times {10}^{-3}\cdot 4,18\times {10}^3\cdot\left(60-26\right)}{\left(26-15\right)}-300\times {10}^{-3}\cdot 4,18\times {10}^3$
$C_{Vase}=38\ J\cdot K^{-1}$

Q7. Sachant que le vase interne a une masse m₁ = 100 g, déterminer sa capacité thermique massique. Commenter le résultat au regard des données fournies.

$C_{Vase}=m_1\cdot c$
$m_1\cdot c=C_{Vase}$
$c=\frac{C_{Vase}}{m_1}$
$c=\frac{38}{100\times {10}^{-3}}$
$c=380\ J\cdot {\rm Kg}^{-1}\cdot K^{-1}$

Remarque : Le matériaux utilisé est certainement l’acier inoxydable qui est adapté au contact alimentaire et bien moins cher que l’argent. La différence trouvée vient certainement des hypothèses faites.

En réalité, les transferts thermiques entre le système {S} et le milieu extérieur ne sont pas inexistants. En effet, une fois l’équilibre thermique atteint, on constate que la température du système diminue au bout de quelques heures.

La    résistance    thermique,    notée    R,    entre    le    système    {S}    et    le   milieu    extérieur    vaut approximativement R = 23 K·W^–1.

Q8. En considérant que le système {S} est à la température de 26 °C et que l’air extérieur est à la température 19 °C, montrer que le flux thermique, noté Φ_ext, du système {S} vers l’extérieur vaut environ 0,3 W.

$\Phi_{ext}=\frac{\left|T_2-T_1\right|}{R}$
$\Phi_{ext}=\frac{\left|26-19\right|}{23}$
$\Phi_{ext}=0,30\ W$

Q9. En déduire l’ordre de grandeur de l’énergie Q_ext échangée par le système {S} avec le milieu extérieur pendant la durée Δt de l’expérience.

$\Phi_{ext}=Q_{ext}\Delta t$
$Q_{ext}\Delta t=\Phi_{ext}$
$Q_{ext}=\Phi_{ext}\times \Delta t$
$Q_{ext}=0,30\times 180$
$Q_{ext}=54\ J$

Q10. Comparer Q_ext à la variation d’énergie interne ΔU_Eau chaude de l’eau chaude introduite dans le vase au cours de l’expérience . Commenter en indiquant si l’hypothèse 1 est justifiée.

$\Delta U_{Eau\ chaude}=m_{EC}\cdot c_E\cdot\left(\theta_{eq}-\theta_{EC}\right)$
$\Delta U_{Eau\ chaude}=100\times {10}^{-3}\cdot 4,18\times {10}^3\cdot \left(26-60\right)$
$\Delta U_{Eau\ chaude}=-1,4\times {10}^4\ J$

$\left|\Delta U_{Eau\ chaude}\right|\gg Q_{ext}$ : la variation d’énergie interne $\Delta U_{Eau\ chaude}$ est très supérieure à l’énergie $Q_{ext}$ échangée par le système {S} avec le milieu extérieur.

L’hypothèse 1 : les transferts thermiques avec le milieu extérieur sont négligés est justifiée.