E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02705, n°G1SPHCH02748 et n°G1SPHCH02781
Télécharger l’exercice en PDF :
Le Blue FireMegacoaster est une attraction de type montagnes russes située dans un parc d’attraction. Elle détient le record du plus haut looping d’Europe sur des montagnes russes lancées.
Dans cette attraction le train est lancé, c’est-à-dire qu’un moteur linéaire lui procure l’énergie cinétique nécessaire pour parcourir l’ensemble de l’attraction avant la première bosse.

Source : d’après https://www.europapark.de/fr
L’objectif de cet exercice est de vérifier la cohérence de certaines informations fournies par le constructeur de l’attraction et notamment d’apporter un regard critique sur la précision des données fournies.
Quelques informations :
La trajectoire que parcourt le train jusqu’au sommet de la première montée est la suivante :
Le schéma est représenté sans souci d’échelle.
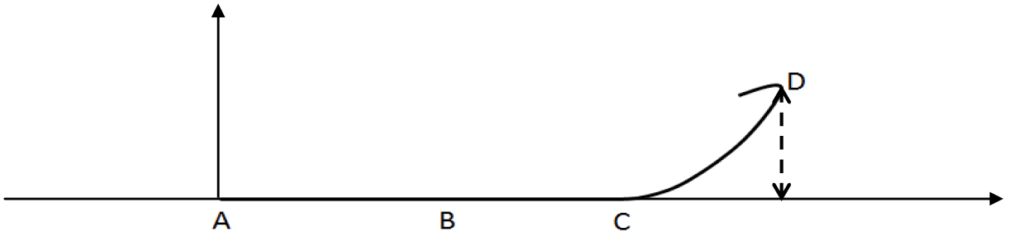
Le train est initialement immobilisé au point A avec la vitesse initiale v0 = 0 m.s – 1. Grâce à un moteur linéaire électrique il est accéléré, sur une piste horizontale, par une force constante entre les points A et B pendant une durée Δt = 2,5 s pour atteindre sa vitesse maximale vmax au point B. À partir du point C, il parcourt la première montée pour atteindre son sommet au point D à une hauteur h = 38 m au-dessus de la piste de lancement.
On considère, en première approximation, que les frottements sont négligeables.
- Quelques caractéristiques de l’attraction :
| Masse du train | m = 10 t |
| Puissance du moteur linéaire | P = 1,5 MW |
| Durée de lancement | Δt = 2,5 s |
| Vitesse maximale | vmax = 100 km.h – 1 |
| Hauteur maximale de l’attraction (par rapport à la piste de lancement) | hmax = 38 m |
Données :
- intensité du champ de pesanteur terrestre : g = 9,81 m×s – 2 ;
- le niveau de référence de l’énergie potentielle de pesanteur est choisi pour l’altitude y = 0 : Epp(A) = 0 J.
1. Étude de la chaine énergétique
1.1. La chaîne énergétique suivante permet de schématiser la conversion d’énergie lors du lancement du train :
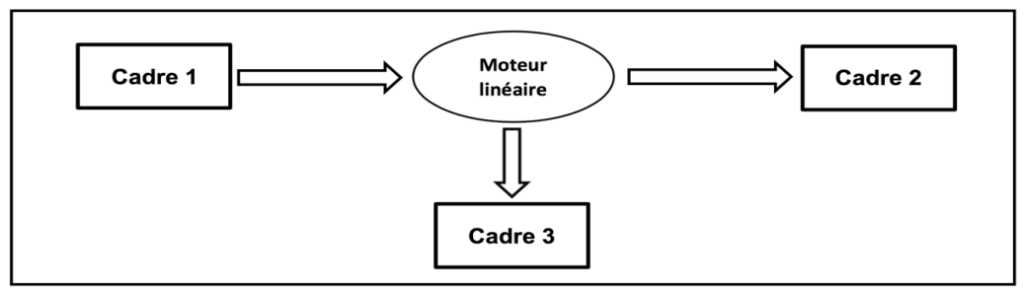
Sans recopier la chaîne énergétique ci-dessus, donner la forme d’énergie à faire apparaître dans chaque cadre numéroté de 1 à 3.
Cadre 1 : Energie électrique
Cadre 2 : Energie mécanique
Cadre 3 : Energie thermique (pertes)
Pour cela, indiquer sur la copie le numéro du cadre et lui associer une forme d’énergie.
1.2. Montrer que l’énergie cinétique du train Etrain à la fin de la phase de lancement vaut Etrain = 3,9 MJ.
$$E_{train}=E_c=\frac{1}{2}\times m\times v^2$$
$$E_{train}=\frac{1}{2}\times 10{.10}^3\times {(\frac{100}{3,6})}^2$$
$$E_{train}=3,9{.10}^6J=3,9MJ$$
1.3.Le rendement du moteur linéaire étant donné par la relation \[\eta=\frac{E_{train}}{E_{électrique}}\] où Eélectrique est l’énergie électrique fournie au moteur linéaire, déterminer la valeur du rendement h. Commenter la valeur obtenue en apportant un regard critique sur les données fournies par le constructeur.
$$\eta=\frac{E_{train}}{E_{electrique}}$$
Or
$$E_{electrique}=P\times \Delta t$$
D’ou
$$\eta=\frac{E_{train}}{P\times \Delta t} $$
$$\eta=\frac{3,9{.10}^6}{1,5{.10}^6\times 2,5}=1,04=104%$$
Le rendement est supérieur a 1 (100%), ce qui est impossible. Les données fournies par le constructeur sont imprécises ou fausses.
2. Simulation de la propulsion du train
Afin d’illustrer la phase de lancement, le programme suivant écrit en langage Python permet de simuler la trajectoire du train ainsi que de tracer les vecteurs variation de vitesse Δv→ en quelques points de cette trajectoire sur une durée Δt. Le modèle utilisé formule l’hypothèse d’un mouvement à accélération constante.
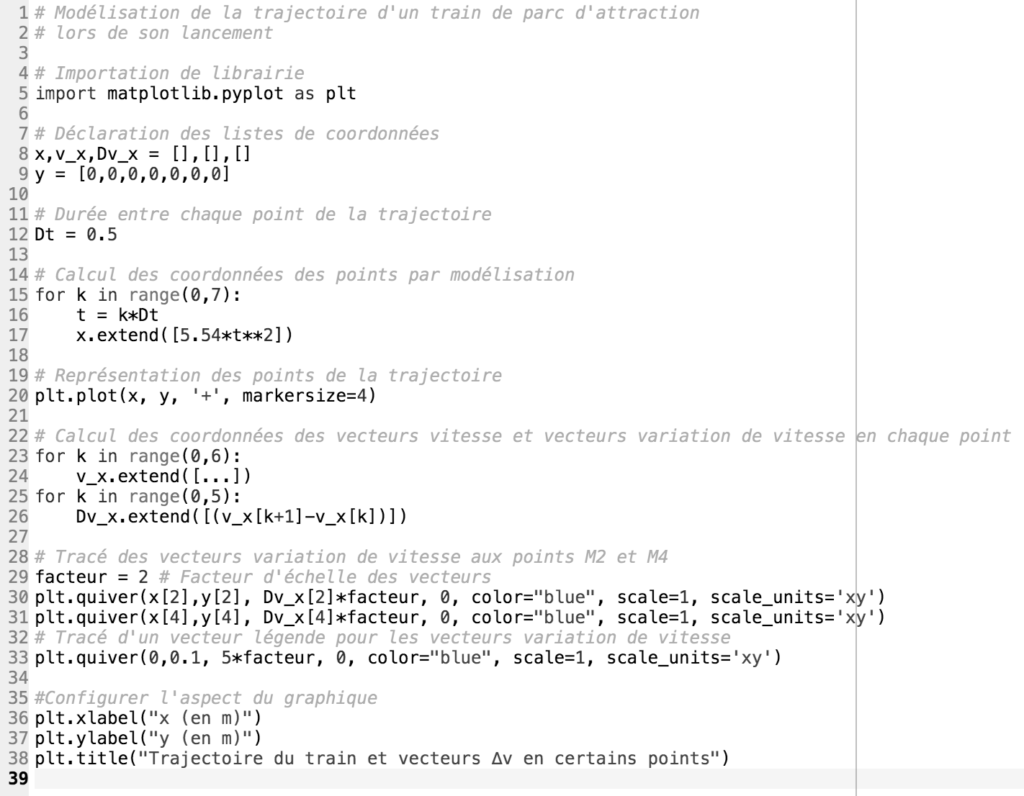
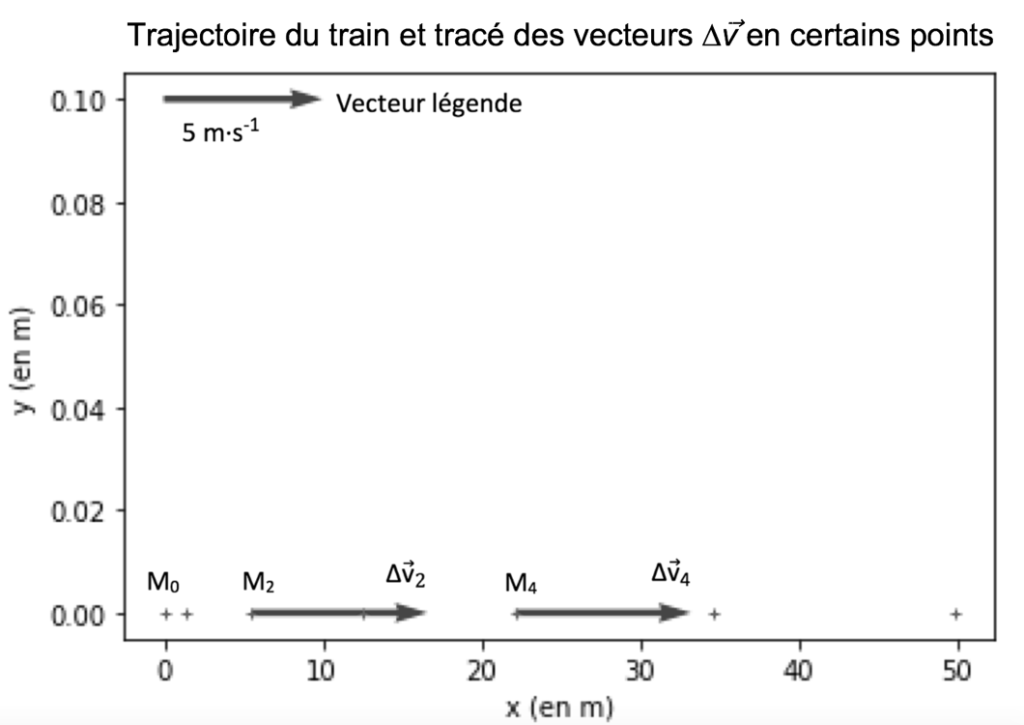
La fenêtre suivante présente le résultat obtenu :
2.1. Compléter la ligne 24 du programme de simulation en modifiant la partie entre les crochets […] afin de calculer les coordonnées vx[k] des vecteurs vitesses aux différents points de la trajectoire.
Il faut calculer la vitesse aux différents points.
La vitesse instantanée se calcule par la formule :
$$v_i=\frac{M_{i+1}M_i}{\Delta t}$$
Avec :
$M_{i+1}M_i$ la distance entre deux points soit : x[k+1]-x[k]
$\Delta t$ le temps entre ces deux points : t[k+1]-t[k]
Ligne 24 : v_x.extend([(x[k+1]-x[k])/(t[k+1]-t[k])])
2.2. Déterminer graphiquement les valeurs Δv2 et Δv4 des normes des vecteurs $\overrightarrow{\Delta v}$ aux points M2 et M4.
Sur le schéma on lit : 1,7 cm correspond à 5 m.s-1
$\Delta v_2$ mesure 1,9 cm soit $\Delta v_2=frac{1,9\times 5}{1,7} =5,6\ m.s^{-1}$
$\Delta v_3$ mesure 1,9 cm soit $\Delta v_3=frac{1,9\times 5}{1,7} =5,6\ m.s^{-1}$
2.3. Expliquer comment semble évoluer le vecteur au cours de la phase de lancement du train.
$\Delta v$ semble être constant. De plus la direction et son sens sont également constants. Ainsi $\Delta v$ semble être constant.
2.4. Donner la relation approchée entre le vecteur variation de vitesse $\overrightarrow{\Delta v}$ du train et la somme des forces $\Sigma\overrightarrow{F}_{ext} $ extérieures qui s’appliquent sur celui-ci.
La relation approchée de la deuxième loi de Newton s’écrit :
$$\Sigma\overrightarrow{F}_{ext}=m\frac{\Delta v}{\Delta t}$$
2.5. En déduire les caractéristiques du vecteur $\Sigma\overrightarrow{F}_{ext} $ .
$$\Sigma\overrightarrow{F}_{ext}=m\frac{\Delta v}{\Delta t}$$
Ainsi $\Sigma\overrightarrow{F}_{ext}$ à la même direction et le même sens que $\Delta v$.
Direction de $\Sigma\overrightarrow{F}_{ext}$ : horizontale
Sens de $\Sigma\overrightarrow{F}_{ext}$ : vers la droite
Calculons sa valeur :
$$\Sigma F=m\frac{\Delta v}{\Delta t}$$
Ligne 12 du programme : Dt=0,5 soit $\Delta t=0,5\ s$
$$\Sigma F=10{.10}^3\times \frac{5,6}{0,5}$$
$$\Sigma F=1,1{.10}^5N$$
3. Étude du train lors de la première ascension
Une modélisation simplifiée de la trajectoire du train, considéré comme un point matériel M, entre les points A et D peut être donnée par le schéma suivant, représenté sans souci d’échelle.
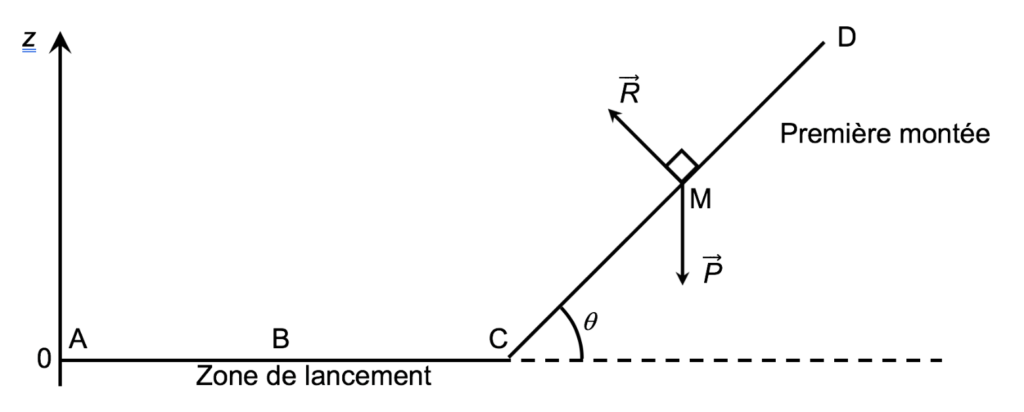
On considère la première montée CD comme rectiligne et faisant un angle q = 45° avec l’horizontale.
Le poids est une force conservative.
3.1. Exprimer le travail $W_{CD}\left(\overrightarrow{P}\right)$ du poids sur le trajet CD en fonction de $\overrightarrow{CD}$ et de $\overrightarrow{P}$ puis montrer que $W_{CD}(\overrightarrow{P})=mg\times(y_C-y_D)$.
$$W_{CD}\left(\overrightarrow{P}\right)=\overrightarrow{P}.\overrightarrow{CD}=P\times CD\times cos(\alpha)\ \ $$
Avec $\alpha$ l’angle entre P et CD
Avec $$\alpha=\theta+\frac{\pi}{2}$$
De plus : $$cos\left(\alpha\right)=cos\left(\theta+\frac{\pi}{2}\right)=-\sin{\left(\theta\right)}\ \ $$
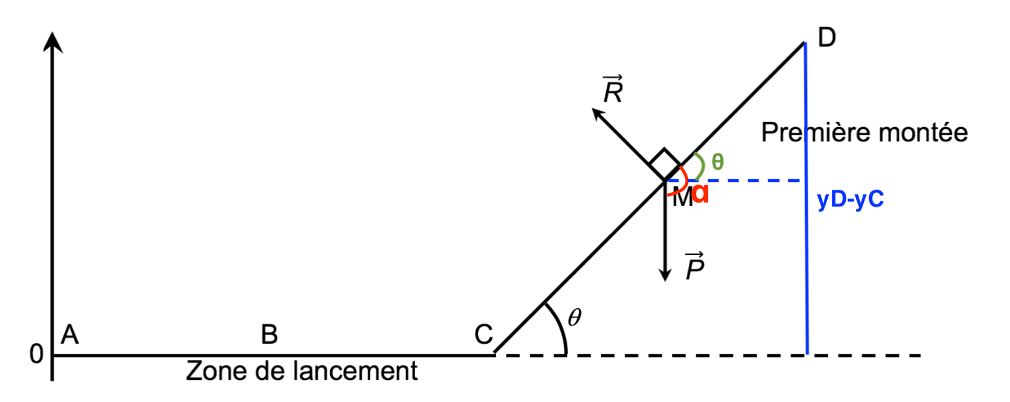
or $$\sin{\left(\theta\right)}=\frac{opposé}{hypothénuse}=\frac{y_D-y_C}{CD}$$
donc
$$W_{CD}\left(\overrightarrow{P}\right)=\ P\times CD\times-\frac{y_D-y_C}{CD}=P\times-(y_D-y_C)$$
$$W_{CD}(\overrightarrow{P})=mg\times-(y_D-y_C)$$
$$W_{CD}(\overrightarrow{P})=mg\times(y_C-y_D)$$
3.2. Donner la valeur du travail $W_{CD}\left(\overrightarrow{R}\right)$ de la force de réaction des rails lors de la première montée. Justifier.
$$W_{CD}\left(\overrightarrow{R}\right)=\overrightarrow{R}.\overrightarrow{CD}=0\ J$$
Car $\overrightarrow{R}$ est perpendiculaire à $\overrightarrow{CD}$
3.3. Établir l’expression de l’altitude maximale hmax que pourrait atteindre le train en l’absence de frottements puis calculer sa valeur. Commenter.
En l’absence de frottements l’énergie mécanique se conserve :
$$E_m\left(D\right)=E_m\left(C\right)$$
$$E_c\left(D\right)+E_{pp}\left(D\right)=E_c\left(C\right)+E_{pp}\left(C\right)$$
Or
$$E_c\left(D\right)=0\ J$$ car il arrive au point D sans vitesse (il ne monte plus).
$$E_{pp}\left(C\right)=0\ J$$ car yc est nul.
Donc
$$E_{pp}\left(D\right)=E_c\left(C\right)$$
$$m\times g\times y_D=\frac{1}{2}\times m\times v_c^2$$
$$y_D=\frac{v_c^2}{2\times g}$$
$$y_D=\frac{{(\frac{100}{3,6})}^2}{2\times 9,81}=39,4\ m$$
L’altitude maximale est de 39,4 m.
La valeur trouvée est supérieure à la valeur indiquée par le constructeur. C’est cohérent avec une situation réelle car nous avons négligé les forces de frottements dans notre calcul.
