Enseignement scientifique première partie mathématique
Durée 0h48 – 12 points
Télécharger l’exercice en PDF :
Une entreprise produit et vend du savon. Le savon est présenté sous deux formes : sous forme de bloc de savon ou sous forme de savon liquide.
Les deux parties de l’exercice peuvent être traitées de manière indépendante.
Partie A Achat par correspondance de blocs de savon
Pour un achat par correspondance, le client paie le prix des savons proportionnel au nombre de savons contenus dans le lot auquel s’ajoute les frais de port fixes c’est-à- dire indépendant du nombre de savons.
Ainsi l’achat par correspondance d’un lot de dix savons coute 31 euros tout compris et celui d’un lot de trente savons 81 euros tout compris.
1- Le prix tout compris est-il proportionnel au nombre de savons ? Pourquoi ?
2-a- Vérifier que le prix d’un savon contenu dans le lot est 2,50 €.
2-b- Quel est le coût total d’un lot de cinquante savons achetés par correspondance ?
2-c- Proposer une formule pour calculer le coût total, noté 𝑐(𝑛), d’un lot de 𝑛 savons, frais de port inclus, où 𝑛 est un entier naturel.
3- Les clients par correspondance les plus fidèles bénéficient d’une réduction permanente de 10 % sur le prix des savons et de 50 % sur les frais de port.
3-a- Quel est le coût total d’une commande par correspondance de trente savons pour un client fidèle ?
3-b- Quel est alors le taux de la remise globale obtenue par un client fidèle pour une commande de trente savons ? On arrondira le résultat à 0,1 %.
Partie B Optimisation de la production de savon liquide
La capacité de production journalière de l’entreprise est de 15 hectolitres de savon liquide. On rappelle qu’un hectolitre est égal à cent litres.
On modélise le coût total, en euro, de fabrication journalière de 𝑥 hectolitres de savon liquide par une fonction 𝐶 telle que :
𝐶(𝑥) = 𝑥3 − 15𝑥2 + 75𝑥 + 100 où 𝑥 ∈ [0; 15].
4- Le responsable de la fabrication estime que les coûts fixes journaliers liés à la production de savon liquide s’élèvent à cent euros. A-t-il raison ?
5- On admet que 𝐶 est dérivable sur [0 ; 15] et on note 𝐶′ la fonction dérivée de la fonction 𝐶.
5-a- Calculer 𝐶′(𝑥) pour tout réel 𝑥 appartenant à [0 ; 15].
5-b- Justifier que 𝐶′(𝑥) peut s’écrire sous la forme 3(𝑥 − 5)2.
5-c- En déduire le sens de variation de la fonction 𝐶 sur [0 ; 15].
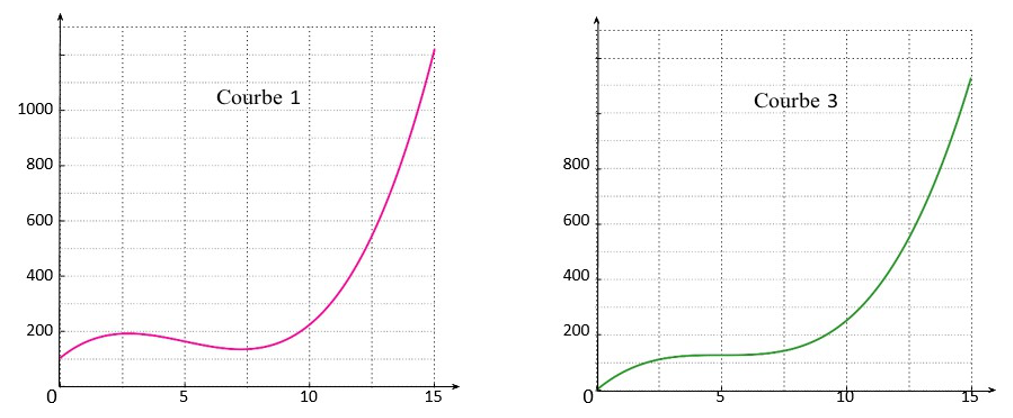
6- On donne sur la page suivante quatre courbes dont l’une est la représentation graphique de la fonction 𝐶 sur [0 ; 15].
6-a- De quelle courbe s’agit-il ? Justifier la réponse donnée.
6-b- Pour des raisons comptables, l’entreprise ne peut engager des coûts de fabrication de plus de 600 euros par jour. Estimer graphiquement, aussi précisément que possible, la capacité de production journalière de savon liquide autorisée, en expliquant la méthode employée.