Four à céramique

Bac Centres étrangers 2023 Sujet 1

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°23-PYCJ1G11

EXERCICE 3 – FOUR À CÉRAMIQUE (5 points)

Pour obtenir des objets en céramique, il faut les placer à l’intérieur d’un four adapté. Les objets sont introduits dans le four à température ambiante, chauffés progressivement jusqu’à atteindre 1000 °C (phase 1) et maintenus à cette température pendant une durée précise pour obtenir une céramique réussie (phase 2).

L’objectif de cet exercice est d’évaluer la consommation de gaz d’un four lors des deux phases de la cuisson.

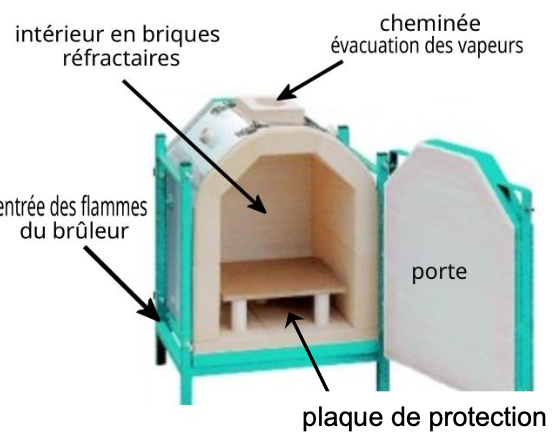
DOCUMENT 1 – Le four

Caractéristiques du four

• Capacité thermique massique : c_f = 800 J·K^-1·kg^-1
• Masse du four : m_f= 120 kg
• Résistance thermique du four : R_th = 0,6 K·W^-1 = 0,6 °C·W^-1

DOCUMENT 2 – Bouteille de propane

Pour la cuisson, on utilise du propane, gaz combustible, dont les caractéristiques sont les suivantes :

• Masse molaire du propane : M = 44,1 g·mol^-1
• Énergie molaire libérée lors de la combustion du propane : E_n = 2004 kJ·mol^-1

Rappels

• T(K) = θ (°C) + 273,15
• La variation de l’énergie interne ΔU d’un système incompressible de masse m et de capacité thermique massique c, dont la température passe de θ_i à θ_f, est donnée par la relation : ΔU = m×c×(θ_f– θ_i).

Données

• Le débit massique de gaz en sortie de bouteille, D, en g·h^-1, est la masse de gaz, en gramme, cédée par la bouteille durant 1 h.
• La résistance thermique est reliée au flux thermique par la relation : $\Phi=\frac{\theta_{four}-\theta_{ext}}{R_{th}}$

avec le flux Φ en watt et la différence de température (θ_four – θ_ext) entre le four et l’air extérieur, en K ou en °C.

Partie A – Durée de la mise en température du four

On veut déterminer la quantité de gaz brûlée dans le four pour élever sa température de θ_i = 20 °C à θ_f = 1000 °C.

1. Calculer la variation d’énergie interne ΔU du système { four } lorsque sa température passe de θ_i à θ_f.

$\Delta U=mf\times cf\times \theta_f-\theta_i$
$\Delta U=120\times 800\times 1000-20$
$\Delta U=9,4\times {10}^7J$

2. Appliquer le premier principe de la thermodynamique au système { four } et en déduire la valeur de la quantité d’énergie Q reçue par le système par transfert thermique.

$\Delta U=Q+W$
Or $W=0$
Donc $\Delta U=Q$
$Q=\Delta U$
$Q=9,4\times {10}^7J$

Lors de la phase de chauffe, la combustion du gaz dégage une quantité de chaleur Q_A supérieure à Q car 33 % de la quantité Q_A est perdue lors de la chauffe.

3. Montrer que la quantité d’énergie thermique Q_A que doit fournir la combustion du gaz a pour valeur Q_A = 1,4×10⁸ J.

D’après l’énoncé : « 33% de QA est perdue lors de la chauffe »
Donc la quantité reçue par le système représente 100-33=67% de QA
$Q=\frac{67}{100}\times Q_A$
$\frac{67}{100}\times Q_A=Q$
$Q_A=\frac{Q}{\frac{67}{100}}$
$Q_A=\frac{9,4\times {10}^7}{\frac{67}{100}}$
$Q_A=1,4\times {10}^8J$

4. Déduire des questions précédentes la valeur de la masse mg de gaz nécessaire pour atteindre la température θ_f.

Energie molaire libérée lors de la combustion du propane :
$E_n=\frac{E}{n}$
Avec $E$ l’énergie soit $E=Q_A$
$E_n=\frac{Q_A}{n}$
$n=\frac{Q_A}{E_n}$
Or
$n=\frac{m_g}{M}$
$m_g=n\times M$

D’ou
$m_g=\frac{Q_A}{E_n}\times M$
$m_g=\frac{1,4\times {10}^8}{2004\times {10}^3}\times 44,1$
$m_g=3,1\times {10}^3\ g$

5. En supposant que, pour cette phase, le débit du gaz en sortie de bouteille est constant et vaut D = 1250 g·h^-1, déterminer la valeur de la durée ∆𝑡𝐴 nécessaire pour que la température du four atteigne la valeur souhaitée.

Le débit est la masse de gaz cédé par la bouteille durant 1h

1250 g	1h
$m_g=3,1\times {10}^3\ g$	$\Delta t_A$

$\Delta t_A=3,1\times {10}^3\times \frac{1}{1250}$
$\Delta t_A=2,5\ h$

Partie B – Maintien en température

Une fois la température de 1000 °C atteinte, la combustion du propane est maintenue pour que le four reste à cette température θ_four = 1000 °C pendant la durée ∆𝑡_𝐵 = 20 min. Le lieu où se trouve le four (milieu extérieur) demeure en permanence à la température θ_ext = 20 °C.

On note Q_B la quantité de chaleur reçue par le système { four }, due à la combustion du propane durant la durée ∆𝑡𝐵, pour compenser les pertes thermiques vers le milieu extérieur.

6. Citer les trois modes de transfert thermique possibles du four vers le milieu extérieur.

Les trois modes de transfert thermiques possibles sont :
La conduction
La convection
Le rayonnement

Le constructeur du four indique une résistance thermique de R_th = 0,60 K·W^-1.

7. Calculer la valeur du flux thermique Φ entre le système { four } et le milieu extérieur lorsque le four est maintenu à θ_four = 1000 °C.

$\phi=\frac{\theta_{four}-\theta_{ext}}{R_{th}}$
$\phi=\frac{1000-20}{0,60}$
$\phi=1,6\times {10}^3W$

Le four est maintenu à cette température pendant la durée ∆𝑡𝐵 = 20 min.

8. Montrer que la valeur de l’énergie Q_B nécessaire pour maintenir constante la température du four pendant cette durée est proche de 2,0 MJ.

$\phi=\frac{Q_B}{\Delta t_B}$
$\frac{Q_B}{\Delta t_B}=\phi$
$Q_B=\phi\times \Delta t_B$
$Q_B=1,6\times {10}^3\times 20\times 60$
$Q_B=1,9\times {10}^6J$
$Q_B=1,9\ MJ$
La valeur de l’énergie $Q_B$ nécessaire pour maintenir constante la température du four pendant cette durée est proche de 2,0MJ.

9. En déduire la valeur de la masse de gaz minimale m_min qui doit être consommée pendant cette phase de maintien de la température du four à θ_four = 1000 °C.

Reprenons la formule de la question 4.
$m_{min}=\frac{Q_B}{E_n}\times M$
$m_{min}=\frac{1,9\times {10}^6}{2004\times {10}^3}\times 44,1$
$m_{min}=42\ g$

Partie C – Comparaison des énergies

10. Comparer la valeur de l’énergie Q_A nécessaire pour la mise en température avec celle de l’énergie Q_B nécessaire pour maintenir le four à température. En tirer une conclusion pratique dans la vie quotidienne lorsque l’on a plusieurs cuissons différentes à réaliser.

$\frac{Q_A}{Q_B}=\frac{1,4\times {10}^8}{1,9\times {10}^6}=74$

L’énergie $Q_A$ nécessaire pour la mise en température est 74 fois plus élevée que l’énergie $Q_B$ nécessaire pour maintenir le four à température.
Ainsi, il est plus intéressant de laisser de faire les différentes cuissons les unes à la suite des autres : on économise alors l’énergie nécessaire pour la mise en température.
Cette économie est non négligeable car elle est très supérieure à celle du maintient de la température.