Géode de galène

Enseignement scientifique première

Durée 1h – 10 points – Thème « Une longue histoire de la matière »

Le plomb est présent à l’état naturel sous diverses formes dans la croûte terrestre. On le trouve principalement dans la galène, qui en contient 86,6 % en masse. Cet élément a permis de donner une estimation précise de l’âge de la Terre.

Partie 1 : la galène

1- La galène est un solide minéral composé en majorité de sulfure de plomb qui possède une structure cristalline de type chlorure de sodium constituée des ions plomb Pb²⁺ et des ions sulfure S^2- (voir document 1 page suivante).

1-a- Déterminer le type de réseau cristallin formé par les ions plomb Pb²⁺.

Le type de réseau cristallin formé par les ions plomb Pb²⁺ est cubique face centrée car les ions plomb Pb²⁺ occupent les sommets et les centre des faces d’une maille.

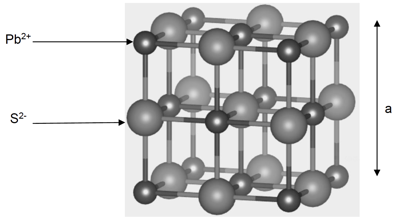
1-b- Préciser les différentes positions occupées par les ions sulfure S^2- dans la maille.

Les ions sulfure S^2- occupent les centre des arrêtes dans la maille et un au centre de la maille.

Document 1 : une maille de la structure cristalline de sulfure de plomb.

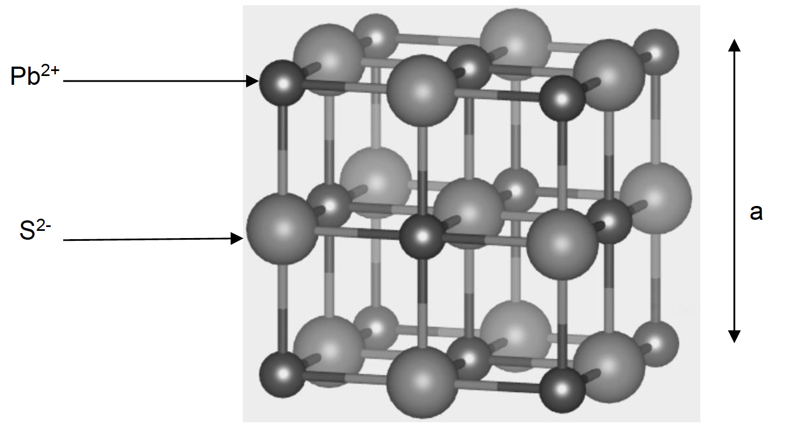
2-a- Justifier qu’il y a quatre ions plomb Pb²⁺ et quatre ions sulfure S^2- dans la maille.

Pour les ions plomb Pb²⁺ :

Il y a 8 ions sur les sommets qui sont dans 1/8 de la maille.

Il y a 6 ions sur les faces qui sont dans 1/2 de la maille.

N=8×1/8+6×1/2=4

Il y a 4 ions plomb Pb²⁺ dans une maille.

Pour les ions sulfure S^2-:

Il y a 12 ions sur les sommets qui sont dans 1/4 de la maille.

Un ion au centre de la maille.

N=12×1/4+1=4

Il y a 4 ions sulfure S^2-dans une maille.

2-b- Choisir la formule chimique du sulfure de plomb parmi les quatre proposées ci- dessous et la recopier sur la copie.

A : Pb₂S B : PbS₂ C : PbS D : PbS₄

Un solide ionique est électriquement neutre : il y a autant d’ions plomb Pb²⁺ que d’ ions sulfure S^2-

C : PbS

3- La forme géométrique de la maille et la nature des ions qui la constituent sont à l’origine des propriétés macroscopiques du cristal, notamment de sa masse volumique.

En utilisant les données ci-dessous, calculer la masse et le volume d’une maille.

En déduire la masse volumique du sulfure de plomb.

Données :

Masse d’un ion plomb Pb²⁺: m_Pb²⁺ = 3,44 × 10^-22 g.

Masse d’un ion sulfure S^2- : m_S^2- = 5,33 × 10^-23 g.

Longueur d’une arête de la maille : a = 5,94 × 10^-8 cm.

$\ m_{maille}=N \times m$

La masse d’une maille :

$\ m_{maille}=N_{Pb^{2+}} \times m_{Pb^{2+}} +N_{S^{2-}} \times m_{S^{2-}}$

$\ m_{maille}=4 \times 3,44.10^{-22} +4 \times 5,33.10^{-23}$

$\ m_{maille}=1,59.10^{-22} g$

le volume d’une maille :

$V_{maille}=a^3$

$V_{maille}=\left(5,94.10^{-8}\right)^3$

$V_{maille}=2,10.10^{-22} cm^3$

$\rho =\frac{m_{maille}}{V_{maille}}$

$\rho =\frac{1,59.10^{-21}}{2,10.10^{-22}}$

$\rho =7,57 g.cm^{-3}$

4- Outre ses utilisations industrielles, la galène peut servir d’objet de décoration. Elle est alors vendue sous forme de géode (cavité rocheuse tapissée de cristaux).

Calculons le pourcentage de géodes dont la masse volumique est comprise entre 7,40 g.cm-3 et 7,60 g. cm-3

Un vendeur de géodes de galène veut estimer la qualité de son stock de géodes. Pour cela, il effectue le prélèvement d’un lot de cinquante géodes dans son stock et détermine la masse volumique de chacune d’elle. Par souci de simplification, il se limite à étudier ce seul critère.

Il obtient les résultats suivants :

Masse volumique (en g.cm^-3)	7,30	7,35	7,40	7,45	7,50	7,55	7,60
Effectif	1	1	9	10	11	13	5

Pour être conforme, un lot de géodes doit contenir au moins 95% de géodes dont la masse volumique est comprise entre 7,40 g.cm^-3 et 7,60 g.cm^-3.

Le lot précédent est-il conforme ? Justifier la réponse.

$P=\frac{9+10+11+13+5}{1+1+9+10+11+13+5}$

P=0,97=97%

Pour être conforme, un lot de géodes doit contenir au moins 95% de géodes dont la masse volumique est comprise entre 7,40 g.cm^-3 et 7,60 g.cm^-3.

Le lot précédent en contient 97% : il est donc conforme.

Partie 2 : détermination de l’âge de la Terre

Dès le XVI^e siècle, les scientifiques ont cherché à déterminer l’âge des roches. C’est la découverte de la radioactivité à la fin du XIX^esiècle qui leur a permis de dater avec une plus grande fiabilité de nombreux échantillons de roches prélevés dans la croûte terrestre.

Document 2 : principe de la datation uranium-plomb

On fait l’hypothèse suivante : on considère qu’il n’y a pas de plomb 206 dans la roche au moment de sa formation, mais qu’elle contient des noyaux d’uranium 238 radioactifs.

On sait qu’un noyau d’uranium 238 radioactif se transforme en un noyau plomb 206 stable à la suite d’une série de désintégrations successives.

L’équation globale est :

${}^{238}_{92}U \rightarrow {}^{206}_{82}Pb+{}^{0}_{-1}e+8{}^{4}_{2}He$

En mesurant la quantité de plomb 206 dans un échantillon de roche ancienne, on peut déterminer l’âge de l’échantillon de roche à partir de la courbe de décroissance radioactive du nombre de noyaux d’uranium 238.

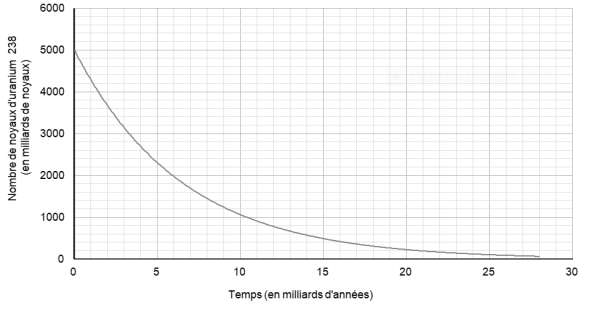
Ainsi, si on considère qu’un échantillon de roche contenant à la fois du plomb 206 et de l’uranium 238 a le même âge que la Terre, il est possible d’utiliser la datation uranium-plomb pour donner une estimation de l’âge de la Terre.

5- Donner la composition d’un noyau de plomb 206.

Composition d’un noyau de plomb 206 :

${}^{206}_{82}Pb$

82 protons

206-82=124 neutrons

6- On note NU(t) et NPb(t) les nombres de noyaux d’uranium 238 et de plomb 206 présents dans l’échantillon à la date t à laquelle la mesure est réalisée et NU(0) le nombre de noyaux d’uranium 238 que contenait la roche au moment de sa formation.

6-a- Justifier la relation NU(0) = NU(t) + NPb(t).

Soit N_U(0) le nombre de noyaux d’uranium 238 que contenait la roche au moment de sa formation.

Or on sait qu’un noyau d’uranium 238 radioactif se transforme en un noyau plomb 206 stable à la suite d’une série de désintégrations successives : le nombre de noyau de plomb créés correspond au nombre de noyau d’uranium qui se sont désintégrés.

Ainsi en additionnant le nombre de noyau restant d’uranium et le nombre de noyaux de plomb nous obtenons le nombre initial de noyau d’uranium :

NU(0) = NU(t) + NPb(t).

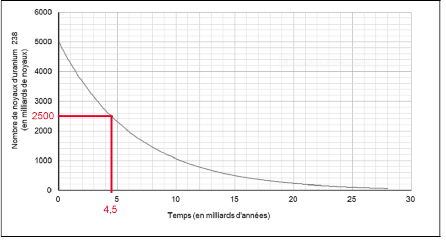
6-b- Déterminer graphiquement NU(0).

Graphiquement NU(0)= 5000 milliards de noyaux

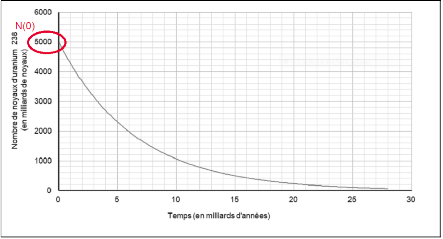
6-c- Le nombre de noyaux de plomb 206 mesuré dans la roche à la date t est égal à N_Pb(t) = 2,5.10¹² noyaux.

Calculer le nombre NU(t) de noyaux d’uranium présents à la date t.

NU(0) = N_U (t) + NPb(t)

NU (t) + NPb(t) = NU(0)

NU (t)= NU(0) – NPb(t)

NU (t)=5000.10⁹– 2,5.10¹²

NU (t) =2,5.10¹²

7- En déduire une estimation de l’âge de la Terre. Expliquer la démarche employée.

NU (t) =2,5.10¹²

NU (t)=2500 milliards de noyaux.

Graphiquement, pour que le nombre de noyau soit de 2500 milliards il faut 4,5 milliard d’années.

En faisant les hypothèses suivantes :

on considère qu’il n’y a pas de plomb 206 dans la roche au moment de sa formation, mais qu’elle contient des noyaux d’uranium 238 radioactifs.
on considère qu’un échantillon de roche contenant à la fois du plomb 206 et de l’uranium 238 a le même âge que la Terre

Il faut 4,5 milliard d’années à l’échantillon pour avoir la proportion d’uranium restante, ainsi l’âge de la terre est estimé à 4,5 milliard d’années.