Histoire de l’âge de la Terre

Sujet avec enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h12 – 12 points – Thème « La Terre, un astre singulier »

On se propose de comprendre de quelle manière on peut connaître l’âge de la Terre.

Partie 1 – La radioactivité des roches, un outil de datation

Document 1 – Principe de la datation absolue

Pour dater de manière absolue les roches, on utilise le principe de décroissance radioactive : au cours du temps, des éléments pères radioactifs se désintègrent en éléments fils, comme représenté ci-dessous

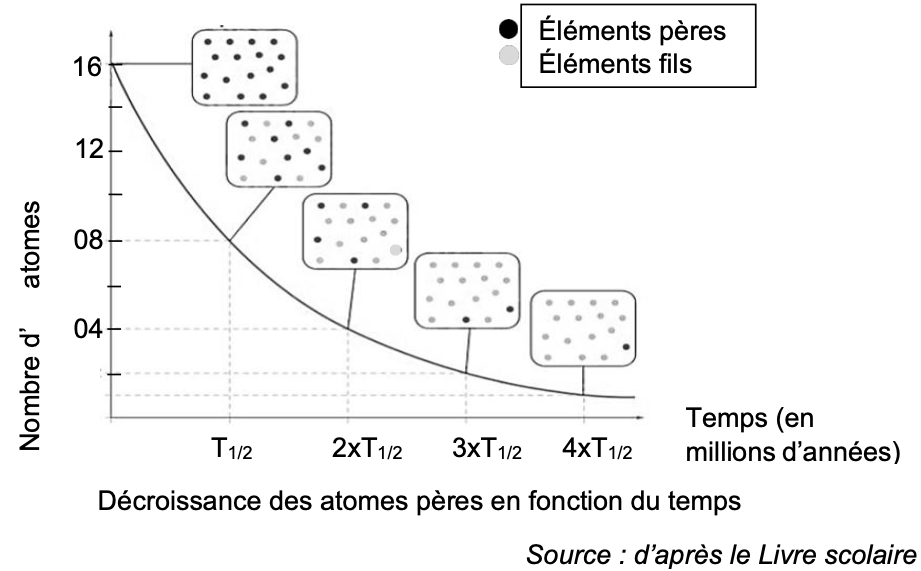
1 – Le temps de demi-vie (ou période radioactive T_1/2) correspond à la durée écoulée lorsqu’une certaine quantité d’éléments pères est désintégrée. À partir du graphique du document 1, dire quelle est la proportion d’éléments pères désintégrée à T_1/2.

Le document 1 nous montre que, au départ il y a 16 atomes pères et qu’au bout d’une durée T_1/2il en reste 8.

Ainsi, la moitié (50%) des éléments pères sont désintégrée au bout d’une durée T_1/2.

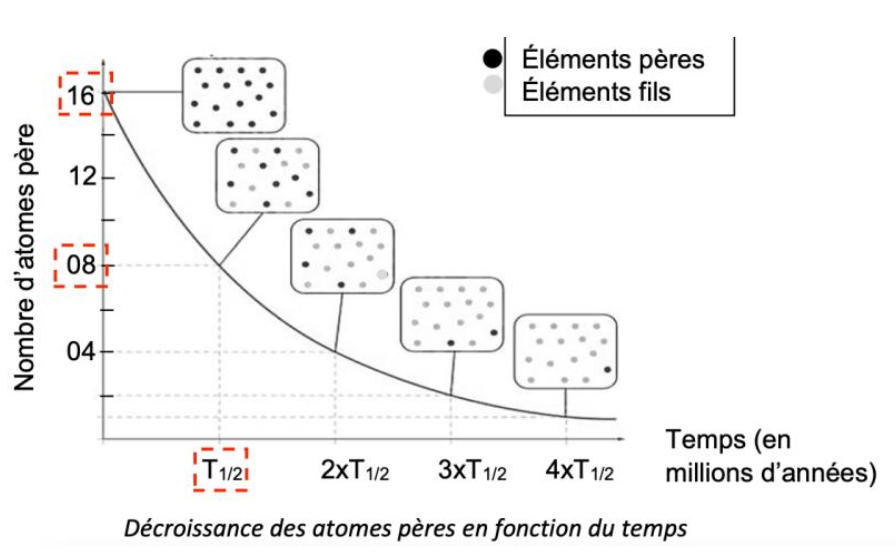
2 – Calculer le pourcentage d’éléments pères encore présents à t = 4xT_1/2. Vous détaillerez votre calcul.

3 – À partir des données du document 1, dire si le taux de désintégration des éléments pères (nombre de noyaux pères disparaissant par unité de temps) est constant avec le temps.

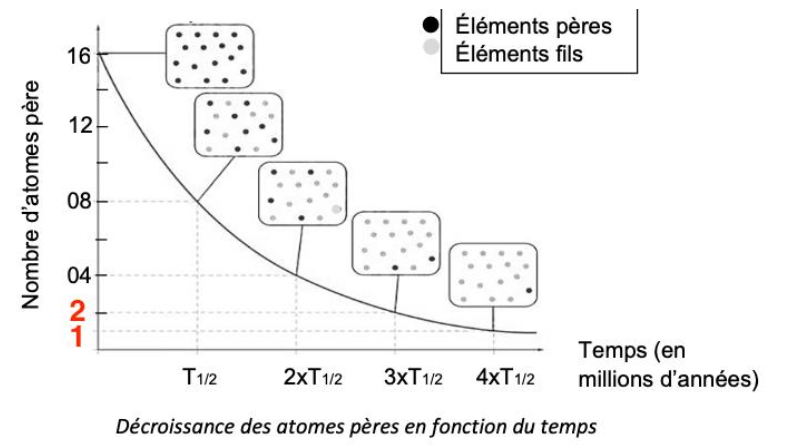
Calculons le nombre de noyaux pères disparu à chaque durée T_1/2 :

Ainsi, le taux de désintégration des éléments pères (nombre de noyaux pères disparaissant par unité de temps) n’est pas constant avec le temps.

Partie 2 – Donner un âge à la Terre : datation sur les météorites et sur les roches terrestres

Pour donner un âge à la Terre, C. Patterson s’appuie sur le « modèle de formation par accrétion » qui admet que les météorites se sont formées en même temps que les planètes du système solaire. En 1955, C. Patterson, met au point une méthode de datation basée sur la mesure des rapports isotopiques du Plomb (Pb). Les deux éléments ²⁰⁷Pb et ²⁰⁶Pb sont issus de la désintégration de l’Uranium (U). L’isotope 204 du plomb est stable et va servir de référence.

Les rapports isotopiques mesurés sur des météorites permettent de tracer une droite nommée “isochrone”.

Document 2 – La méthode de Clair Patterson

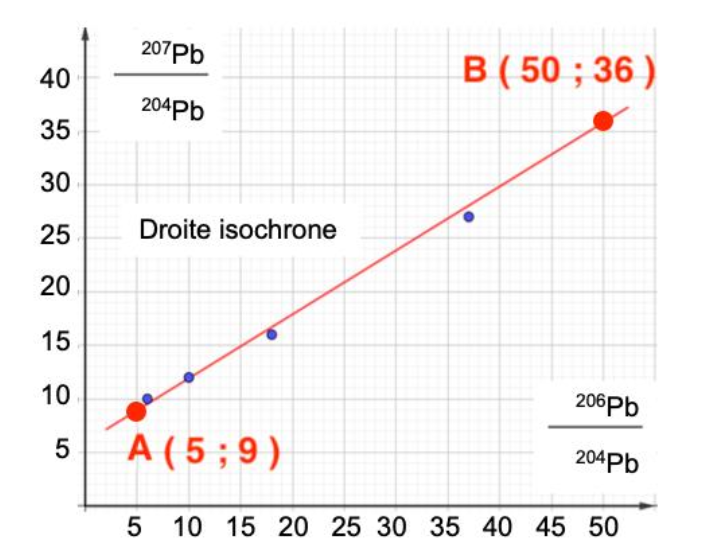
La droite isochrone obtenue par C. Patterson est représentée ci-dessous. Les points correspondent aux rapports isotopiques mesurés sur des météorites. Ces points sont alignés sur une même droite car ils représentent des échantillons de même âge. Le coefficient directeur “m” de cette droite est directement lié à l’âge des météorites.

2a – La droite isoschrone de C. Patterson

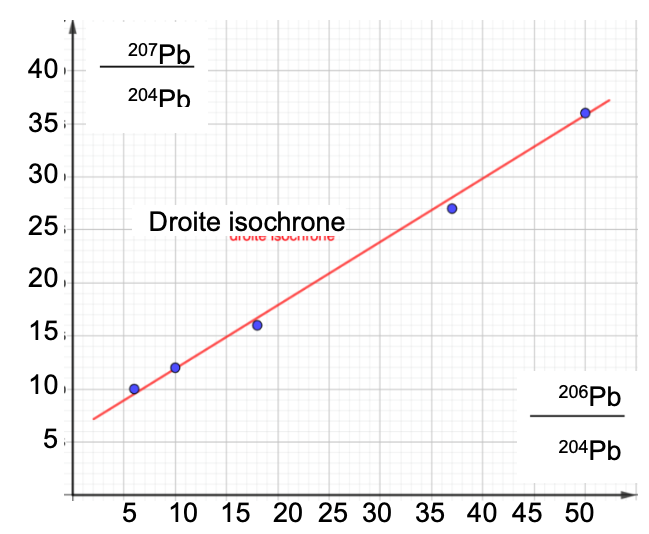
Le coefficient directeur “m” est donné par la relation :

$m=\frac{y_B-y_A}{x_B-x_A}$

avec A (x_A;y_A) et B (x_B;y_B) deux points appartenant à la droite.

Droite isochrone obtenue par Patterson sur des échantillons de météorites.

2b – Graphique représentant un géochronomètre

En utilisant le géochronomètre ci-dessous, il est possible de déterminer graphiquement l’âge d’une roche ou d’un ensemble de roches de même âge grâce à la valeur du coefficient directeur « m » de la droite isochrone.

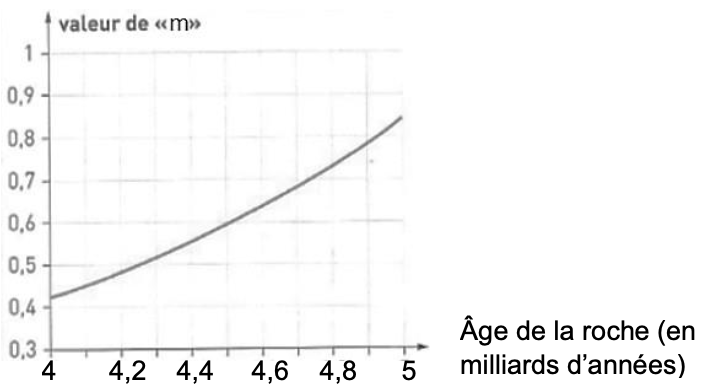
Source : D’après http://acces.ens-lyon.fr/

4 – À partir du document 2, déterminer l’âge des météorites en appliquant la méthode de Patterson. Faire apparaître tous les calculs et les étapes du raisonnement.

Calculons le coefficient directeur “m” :

$m=\frac{y_B-y_A}{x_B-x_A}$

$m=\frac{36-9}{50-5}$

m=0,6

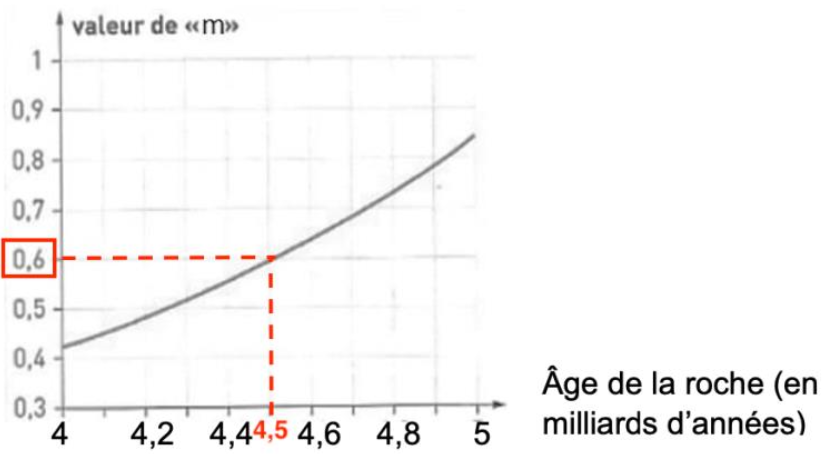
Utilisons le Graphique 2b pour déterminer l’âge des météorites en appliquant la méthode de Patterson :

Graphiquement pour m=0,6, l’âge de la roche est de 4,5 milliards d’années.

Document 3 – Comparaison de radiochronomètres isotopiques

On considère que les résultats obtenus par radiochronologie sont fiables pour des durées allant du millième de la demi-vie à dix fois celle-ci.

	Radiochronomètre Isotope père ‭→ Isotope fils	Demi-vie (T_1/2) en années
Méthode Azote – Béryllium	¹⁴N → ¹⁰Be	1.4 x 10⁶
Méthode Uranium – Plomb	²³⁸U → ²⁰⁶Pb	4.47 x 10⁹

5 – À partir du document 3 et de vos connaissances, justifier l’emploi radiochronomètre isotopique de Patterson (méthode Uranium Plomb) plutôt qu’une autre méthode qui serait basée sur la désintégration radioactive du ¹⁴N.

D’après le document 3 : On considère que les résultats obtenus par radiochronologie sont fiables pour des durées allant du millième de la demi-vie à dix fois celle-ci.

Calculons l’intervalle de fiabilité des différentes méthodes :

1,4 \times{10}^6 \times\frac{1}{1000}=1,4 \times{10}^3

L’âge de la roche est de 4,5 milliards d’années = 4,5×10⁹ années.

Cette valeur est dans l’intervalle de fiabilité de la Méthode Uranium – Plomb mais pas dans celle de la Méthode Azote – Béryllium.

C’est pourquoi on utilise le radiochronomètre isotopique de Patterson (méthode Uranium Plomb) plutôt qu’une autre méthode qui serait basée sur la désintégration radioactive du ¹⁴N.

Document 4 – Zircon de Jack Hills en Australie, daté à 4.4 Milliards d’années

La plupart des roches terrestres anciennes ont disparu à cause de l’érosion et de la tectonique des plaques. Quelques-uns des minéraux qu’elles contiennent, appelés zircons, présentent une résistance importante. Les zircons sont les plus anciens minéraux retrouvés sur Terre.

Source : FuturaSciences

6 – Comparer l’âge du zircon de Jack Hills avec l’âge de la Terre établi grâce à la méthode de Patterson, puis expliquer en quoi il est plus fiable de dater la formation de la Terre à l’aide de mesures réalisées sur des météorites plutôt qu’en utilisant des roches terrestres.

D’après le document 4 – Zircon de Jack Hills en Australie, daté à 4.4 Milliards d’années et l’âge de la Terre l’âge de la Terre établi grâce à la méthode de Patterson est de 4,5 Milliards d’années. Ces deux valeurs sont très proches.

D’après le document 4 La plupart des roches terrestres anciennes ont disparu. C’est pourquoi il est plus fiable de dater la formation de la Terre à l’aide de mesures réalisées sur des météorites plutôt qu’en utilisant des roches terrestres.

Partie 3 – Histoire de l’âge de la Terre

Document 5 – âge estimé de la Terre en fonction des années

Le graphique ci-dessous représente les âges donnés à la Terre par quelques auteurs au cours de notre Histoire.

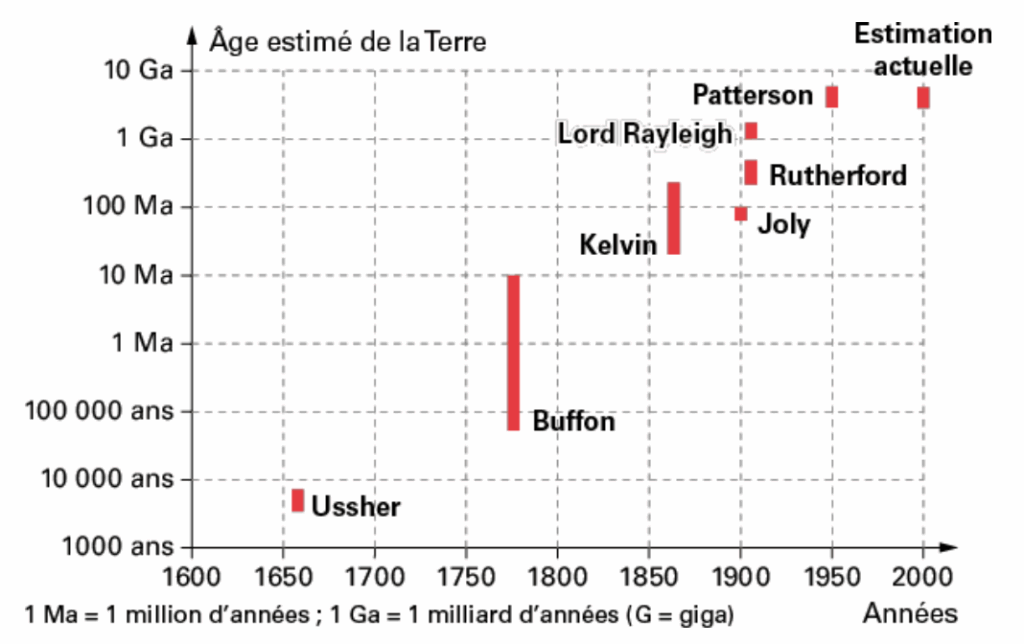
Source : Le livre scolaire

7 – En utilisant les données du document 4 et vos connaissances, commentez brièvement la proposition suivante : « les théories scientifiques ne sont que des théories, elles peuvent toujours changer ». Préciser en particulier comment la communauté scientifique procède pour valider une théorie.

La proposition « les théories scientifiques ne sont que des théories, elles peuvent toujours changer » souligne une caractéristique fondamentale de la science : sa capacité à évoluer en fonction des nouvelles découvertes et des avancées de la recherche.

Les théories scientifiques sont des modèles basés sur des observations, des expériences et des analyses. Elles sont sujettes à révision et à modification lorsque de nouvelles preuves émergent.

La validation d’une théorie scientifique se fait par un processus rigoureux de validation et de réplication. La communauté scientifique utilise des méthodes expérimentales, des observations et des tests pour vérifier la validité d’une théorie.

Si une théorie résiste à ces tests et est capable d’expliquer de manière cohérente le phénomène observé, elle est acceptée comme valide. Cependant, cela ne signifie pas qu’elle est considérée comme définitivement vraie. Elle demeure toujours ouverte à être remise en question ou améliorée avec de nouvelles découvertes.

Le document 5 en est un exemple : l’âge de la Terre donné par la communauté scientifique a évolué au cours du temps.

Temps	Pourcentage d’éléments pères encore présents
Initialement : t =0	100 %
t= T_1/2	$\frac{100}{2}=50\ %$
t= 2xT_1/2	$\frac{50}{2}=25\ %$
t= 3xT_1/2	$\frac{25}{2}=12,5\ %$
t= 4xT_1/2	$\frac{12,5}{2}=6,25\ %$

Temps	Pourcentage d’éléments pères encore présents	Nombre d’éléments pères encore présents	Nombre de noyaux pères disparu
Initialement : t =0	100 %	16
t= T_1/2	$\frac{100}{2}=50\ %$	$\frac{16}{2}=8$	16-8=8
t= 2xT_1/2	$\frac{50}{2}=25\ %$	$\frac{8}{2}=4$	8-4=4
t= 3xT_1/2	$\frac{25}{2}=12,5\ %$	$\frac{4}{2}=2$	4-2=2
t= 4xT_1/2	$\frac{12,5}{2}=6,25\ %$	$\frac{2}{2}=1$	2-1=1

Méthode	Demi-vie (T_1/2) en années	Millième de la demi-vie en années	Dix fois la demi-vie en années	Intervalle de fiabilité en années
Méthode Azote – Béryllium	$1,4 \times {10}^6$	$1,4 \times{10}^6 \times\frac{1}{1000}=1,4 \times{10}^3$	$1,4 \times {10}^6\times 10=1,4 \times {10}^7$	$1,4\times{10}^3<t<1,4\times{10}^7$
Méthode Uranium – Plomb	$4,47 \times {10}^9$	$4,47 \times {10}^9 \times \frac{1}{1000}=4,47 \times {10}^6 }$	$4,47\times {10}^9\times 10=4,47\times {10}^{10}$	$4,47 \times {10}^6<t<4,47 \times {10}^{10}$