Nouvelle Calédonie 2022 Sujet 1
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n° 22-PYCJ1NC1
Sujet et corrigé
Ingenuity est un petit hélicoptère – comparable à un drone – d’un peu moins de deux kilogrammes, développé par l’agence spatiale américaine, la NASA. Il a été expérimenté sur le sol de la planète Mars au cours de la mission Mars 2020 pour tester ses capacités dans le domaine de la reconnaissance optique du sol martien.
Les défis technologiques sont grands :
- l’atmosphère de Mars est peu dense, ce qui limite la portance* des hélices ;
- les délais de communication entre la Terre et Mars interdisent le contrôle de l’hélicoptère en temps réel depuis la Terre, et imposent un système de pilotage automatique programmable à distance.
Le premier vol d’Ingenuity a été réalisé avec succès le lundi 19 avril 2021. Durant ce test d’une durée de 39 secondes, l’hélicoptère s’est élevé de 3 mètres puis a effectué un vol stationnaire avant de se reposer. Une dizaine de vols de plus en plus complexes ont suivi.
- Pour pouvoir voler, les pâles en rotation de l’hélicoptère génèrent une force verticale ascendante appelée « portance ».

source : d’après fr.m.wikipedia.org/wiki, fichier Mars_helicopter_on_sol_46.png
Données :
- Caractéristiques techniques de l’hélicoptère Ingenuity (figure 1 ci-dessus) ;
- Pression atmosphérique de l’air sur Terre : 1,013 × 105 Pa ;
- Masse molaire moyenne de l’air sur Terre : 29,0 × 10-3 kg ∙ mol-1 ;
- Constante des gaz parfaits : 8,314 J ∙ K-1 ∙ mol-1 ;
- Conversion d’unité de température : T(K)=T(°C) + 273,15 ;
- Intensité de pesanteur sur Mars : gM= 3,7 m∙s-2 ;
- Intensité de pesanteur sur Terre : gT= 9,8 m∙s-2 ;
- Pour un gaz supposé parfait, on a la relation : PV=nRT, avec P en pascal (Pa),V en m3, n en mol, R (donné ci-dessus) et T en kelvin (K).
Cet exercice comporte 4 parties indépendantes.
PARTIE A : L’atmosphère de Mars
L’hélicoptère Ingenuity est fortement handicapé dans l’atmosphère peu dense de Mars. En effet, la densité de l’atmosphère est 100 fois plus faible sur Mars que sur Terre.
A.1. En supposant que l’air est un gaz parfait, montrer que la masse volumique de l’air (en kg ∙ m–3) sur Terre ρTerre vérifie la relation :
$\rho_{Terre}= \frac{PM}{RT} $
$$\rho_{Terre}=\frac{m}{V}$$
Or $n=\frac{m}{M}$ donc $m=n\times M$
D’où
$$\rho_{Terre}=\frac{n\times M}{V}$$
Or $PV=nRT$ donc $n=\frac{PV}{RT}$
D’où
$$\rho_{Terre}=\frac{\frac{PV}{RT}\times M}{V}$$
$$\rho_{Terre}=\frac{PV\times M}{RTV}$$
$$\rho_{Terre}=\frac{PM}{RT}$$
A.2. Calculer sa valeur pour une température de l’air de 15 °C .
$$\rho_{Terre}=\frac{PM}{RT}$$
$$\rho_{Terre}=\frac{1,013\times 10^5\times 29,0\times 10^{-3}}{8,314\times \left(15+273,15\right)}$$
$$\rho_{Terre}=1,22\ \mathrm{Kg.m}^{-3}$$
La masse volumique de l’atmosphère sur Mars est égale à 1 % de celle de l’air sur Terre.
A.3. En déduire la valeur de la masse volumique de l’atmosphère sur Mars ρMarc à la température de 15 °C.
$$\rho_{Mars}=1%,\rho_{Terre}$$
$$\rho_{Mars}=\frac{1}{100}\times 1,22$$
$$\rho_{Mars}=1,22\times 10^{-2}\ \mathrm{Kg.m}^{-3}$$
D’après l’énoncé : la masse volumique de l’atmosphère de Mars est égale à 1% de celle de l’air sur Terre.
A.4. Sachant que la portance est proportionnelle à la masse volumique de l’atmosphère dans laquelle se trouve l’engin, expliquer pourquoi c’est un « défi technologique » de faire voler un hélicoptère sur Mars.
Sachant que la portance est proportionnelle à la masse volumique de l’atmosphère dans laquelle se trouve l’engin, la portance sur Mars doit être 100 fois plus grande que celle nécessaire pour faire voler l’engin sur Terre. Ainsi c’est un défi technologique de faire voler un hélicoptère sur Mars.
PARTIE B : La phase de décollage
Pour pouvoir décoller, la portance doit au moins compenser le poids de l’hélicoptère.
Les figures suivantes, sur Terre (figure 2) et sur Mars (figure 3), représentent l’évolution de la portance de l’hélicoptère Ingenuity en fonction de la vitesse de rotation des pâles N en tours par minute (tpm).
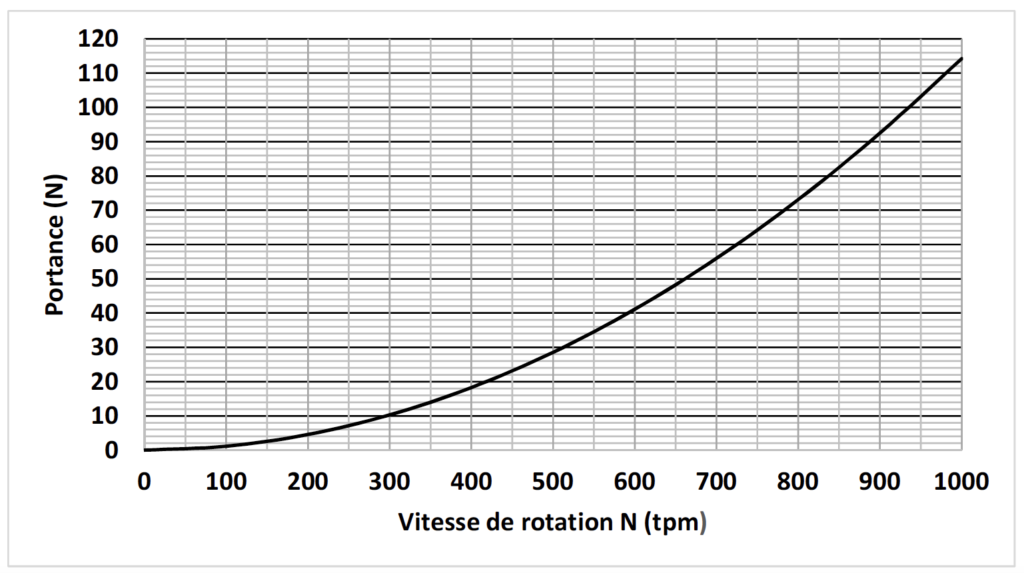
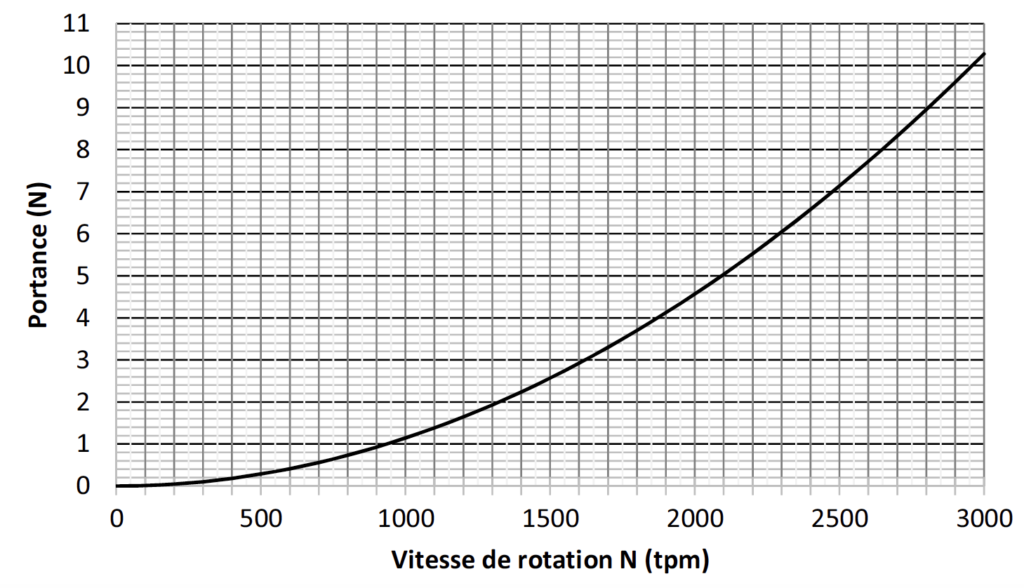
B.1. Déterminer la valeur de la vitesse de rotation minimale des pâles de Ingenuity sur Terre et sur Mars afin que l’hélicoptère décolle. Commenter le résultat.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
D’après l’énoncé : pour pouvoir décoller, la portance doit au moins compenser le poids de l’hélicoptère.
Calculons le poids de l’hélicoptère :
$$P_{Terre}=m\times g_{Terre}$$
$$P_{Terre}=1,8\times 9,8$$
$$P_{Terre}=18\ \mathrm{N}$$

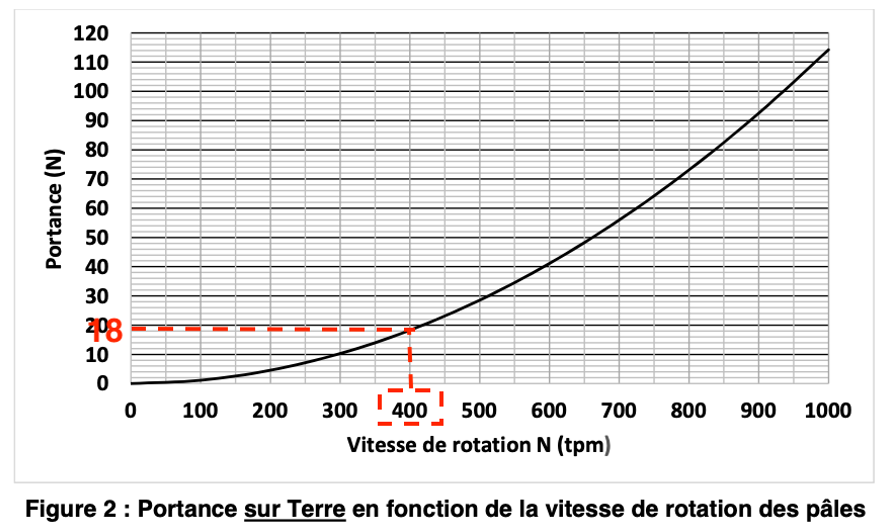
La portance est égale au poids donc $Portance=P_{Terre}=18\ \mathrm{N}$.
Pour une portance de $18\ \mathrm{N}$, la valeur de rotation minimale des pâles de Ingenuity sur Terre est de $400\ \mathrm{tpm}$.
$$P_{Mars}=m\times g_{Mars}$$
$$P_{Mars}=1,8\times 3,7$$
$$P_{Mars}=6,7\ \mathrm{N}$$
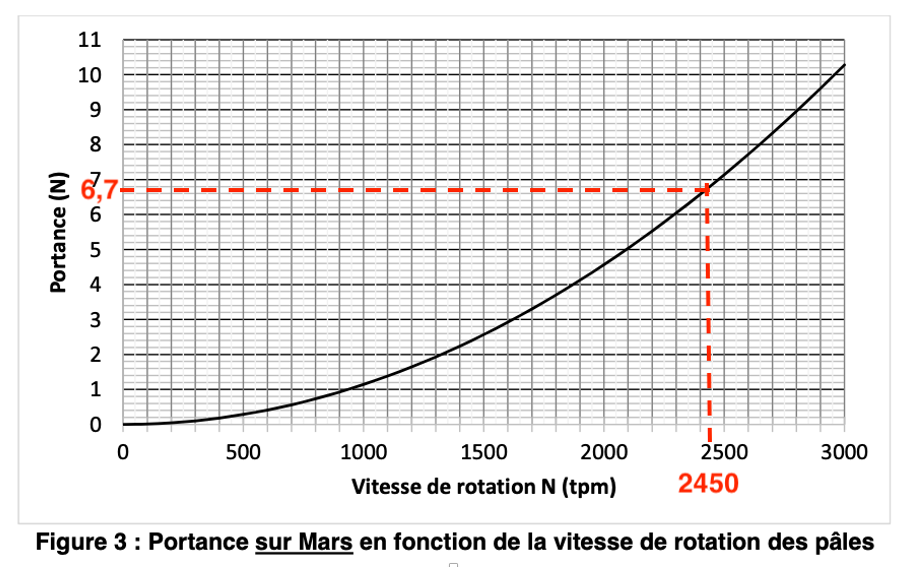
La portance est égale au poids donc $Portance=P_{Mars}=6,7\ \mathrm{N}$.
Pour une portance de $6,7\ \mathrm{N}$, la valeur de rotation minimale des pâles de Ingenuity sur Mars est de $2540\ \mathrm{tpm}$.
PARTIE C : Une phase d’atterrissage délicate
La phase la plus délicate du vol de l’hélicoptère est l’atterrissage, du fait des turbulences qui peuvent déséquilibrer l’engin. La solution retenue est d’arrêter la propulsion à un mètre au-dessus du sol, et de laisser l’hélicoptère atteindre le sol en chute libre
On suppose dans l’étude qui suit que l’hélicoptère Ingenuity est en vol stationnaire – c’est-à-dire à vitesse nulle – à une altitude H = 1,0 m au-dessus du sol martien lorsque ses pâles cessent de tourner. Il chute alors verticalement.
Soit un axe Oz vertical, orienté positivement vers le haut et dont l’origine O est confondue avec le sol (figure 4 ci- contre).
On note $\overrightarrow{g_M}$ le champ de pesanteur sur Mars.
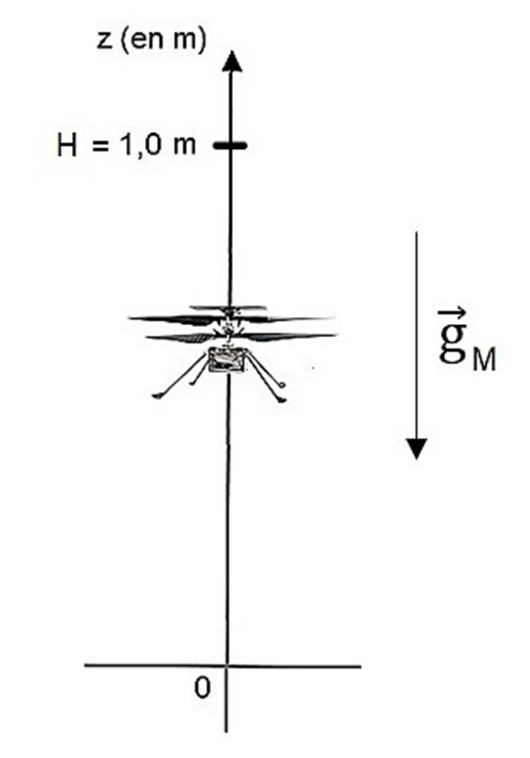
Figure 4 : Atterrissage d’Ingenuity
C.1. Appliquer la deuxième loi de Newton afin d’exprimer la coordonnée az(t) du vecteur accélération de l’hélicoptère lors de la phase de chute libre.
Réponse :
Système {hélicoptère}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$\sum_{}^{}\overrightarrow{F}_{ext}=m\overrightarrow{a}$
$\overrightarrow{P}=m\overrightarrow{a}$
$m\overrightarrow{g}_M=m\overrightarrow{a}$
$\overrightarrow{a}=\overrightarrow{g}_M$
Or
$\overrightarrow{g} \begin{cases} 0 \\-g_M \end{cases}$
$\overrightarrow{a} \begin{cases} a_{x}(t)=0 \\a_{z}(t)=-g_M \end{cases}$
$a_{z}(t)=-g_M $
C.2. En déduire, dans le repère défini, la coordonnée vz(t) du vecteur vitesse de l’hélicoptère lors de la phase de chute libre.
Réponse :
$a_{z}(t)=\frac{d \v_{z}(t)}{dt}$
On intègre $a_{z}(t) $ :
$v_{z}(t)=-gt_M+C_{1}$
Pour trouver les constantes, on utilise $v_{0z}$ :
$v_{0z}=0$
d’ou
$v_{z}(t)=-gt_M$
C.3. Déduire des résultats précédents l’équation horaire z(t) du mouvement de l’hélicoptère lors de la phase de chute libre.
Réponse :
$v_{z}(t)=\frac{d z(t)}{dt}$
On intègre $v_{z}(t)$:
$z(t)=-\frac{1}{2}gt^2+ C_{2}$
Pour trouver les constantes, on utilise $z_0$
$z_0=H$
d’ou
$z(t)=-\frac{1}{2}gt^2+H$
C.4. Déterminer la durée tsol au bout de laquelle l’hélicoptère atteindra le sol martien.
$t_{sol}$ tel que $z\left(t_{sol}\right)=0$ :
$$-\frac{1}{2}g_M t_{sol}^2+H=0$$
$$t_{sol}=\sqrt{\frac{2H}{g_M}}$$
$$t_{sol}=\sqrt{\frac{2\times 1,0}{3,7}}=0,74\ \mathrm{s}$$
C.5. Déterminer la vitesse vsol de l’hélicoptère au moment de l’impact sur le sol martien.
À $t_{sol}$ :
$$v_{sol}=-g_M t_{sol}=-3,7\times 0,74=-2,7\ \mathrm{m.s}^{-1}$$
Le signe négatif indique que la vitesse est orientée vers le bas.
$$|v_{sol}|=2,7\ \mathrm{m.s}^{-1}$$
Lors des essais préparatoires réalisés sur Terre, des vitesses d’impact de l’ordre de grandeur de 16 km ∙ h–1 ont été enregistrées. Le train d’atterrissage d’Ingenuity a été conçu pour résister à de telles vitesses.
C.6. Indiquer, en justifiant, si le train d’atterrissage est assez résistant pour une utilisation sur la planète Mars.
$$|v_{sol}|=2,7\times 3,6=9,7\ \mathrm{km.h}^{-1}$$
Cette vitesse est inférieure aux vitesses d’impact de $16\ \mathrm{km.h}^{-1}$ qui ont été enregistrées. Le train d’atterrissage est assez résistant pour une utilisation sur la planète Mars.
PARTIE D : Mesure de l’altitude au cours d’un vol
Les capteurs embarqués par Ingenuity comprennent une caméra de navigation noir et blanc, une caméra couleur haute résolution, une centrale à inertie, un inclinomètre et un altimètre. Ce dernier capteur permet à Ingenuity de connaître en temps réel son altitude par rapport au sol.
Un groupe d’élèves de lycée souhaite réaliser un altimètre pour un drone à l’aide d’un condensateur dont la capacité C varie en fonction de l’altitude z à laquelle se trouve le drone.
Afin d’étudier les caractéristiques du condensateur choisi, on le place dans le circuit représenté sur la figure 5 :
- l’interrupteur est d’abord en position 1 : le condensateur se charge sous la tension E;
- lorsque la charge est terminée, l’interrupteur bascule en position 2 : le condensateur de capacité C se décharge alors dans la résistance R = 1,0 kΩ.
On se place dans un premier temps dans le cas où le drone, donc le condensateur, se trouve au niveau du sol.
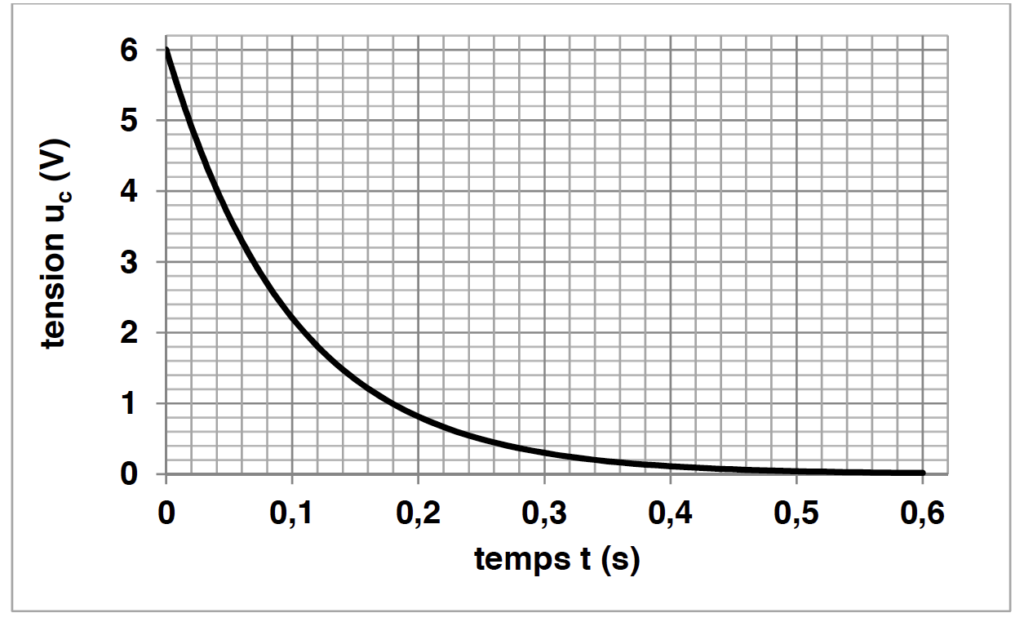
Le graphique de la figure 6 représente l’évolution de la tension uc aux bornes du condensateur au cours de la décharge en fonction du temps.
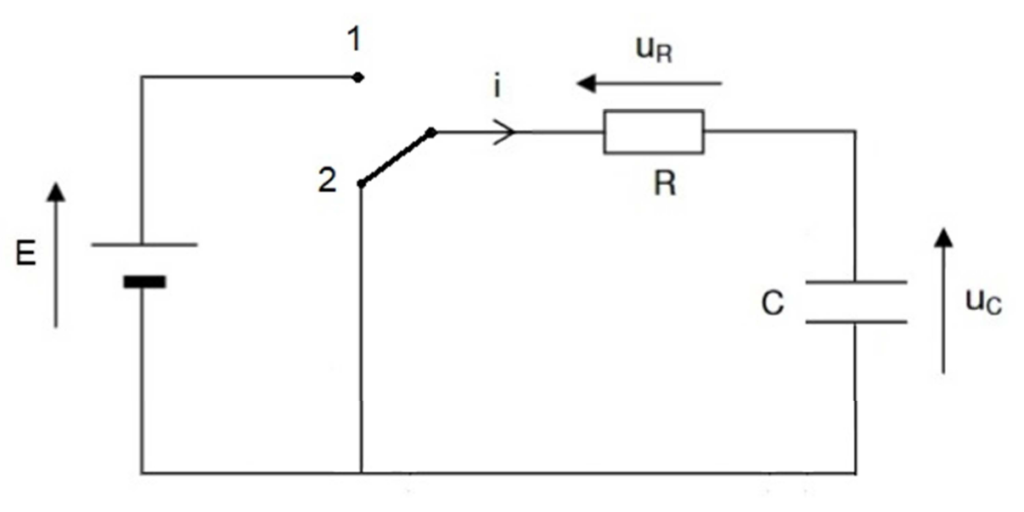
Figure 5 : Schéma du circuit électrique
D.1. Montrer que l’équation différentielle qui régit l’évolution de la tension aux bornes du condensateur lors de sa décharge (interrupteur en position 2) s’écrit :
$\frac{u_C}{dt}+\frac{u_C}{RC }=0 $
Réponse :
D’après la loi d’additivité des tensions ou loi des mailles :
$U_C(t)+U_R(t)=0$
Or $U_R(t)=R \times i$
$U_C(t)+R \times i=0$
Or $ i(t)=\frac{dq(t)}{dt}$
$U_C(t)+R \times \frac{dq(t)}{dt}=0$
Or $q(t)=C \times U_C(t)$
$U_C(t)+R \times \frac{C \times U_C(t)}{dt}=0$
$U_C(t)+RC \times \frac{U_C(t)}{dt}=0$
On divise par RC :
$\frac{u_C}{dt}+\frac{u_C}{RC }=0 $
D.2. Montrer que la solution de cette équation différentielle s’écrit $ u_C(t) = E\times e^{-\frac{t}{\tau}} $ ou τ est le temps caractéristique de cette décharge à exprimer fonction de R et C.
Méthode 1 : on pose $U_C(t)=E,e^{-t/\tau}$
$$\frac{dU_C}{dt}=E\left(-\frac{1}{\tau}\right)e^{-t/\tau}$$
En remplaçant :
$$E e^{-t/\tau}\left(-\frac{1}{\tau}+\frac{1}{RC}\right)=0\Rightarrow \tau=RC$$
Donc $U_C(t)=E e^{-t/\tau}$ est solution avec $\tau=RC$.
Méthode 2 : forme $y’ = ay+b$
Ici $a=-\frac{1}{RC}$, $b=0$ donc
$$U_C(t)=K e^{-t/(RC)}$$
Avec $U_C(0)=E\Rightarrow K=E$ :
$$U_C(t)=E e^{-t/\tau},\ \tau=RC$$
D.3. Déterminer, à l’aide du graphe de la figure 6, et en justifiant la réponse :
D.3.1. la valeur de la tension E ;
$U_C(0)=E$ ; par lecture graphique : $E=6,0\ \mathrm{V}$.
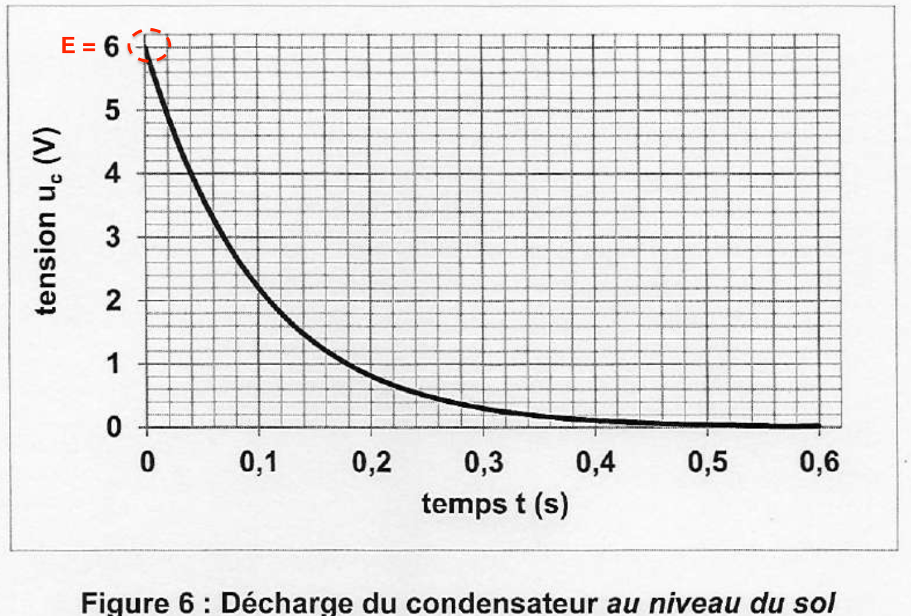
D.3.2. la valeur du temps caractéristique τ.
$\tau$ par tangente en $t=0$ (décharge) :
$$\tau=0,1\ \mathrm{s}$$

D.4. En déduire que la capacité du condensateur au niveau du sol vaut environ C0 = 100 μF.
$$\tau=RC\Rightarrow C=\frac{\tau}{R}=\frac{0,1}{1,0\times 10^3}=1,0\times 10^{-4}\ \mathrm{F}=100\ \mu\mathrm{F}$$
Lorsque le drone monte, la pression atmosphérique diminue et provoque une augmentation de l’épaisseur e entre les armatures comme illustré sur les figures 7 et 8 suivantes.
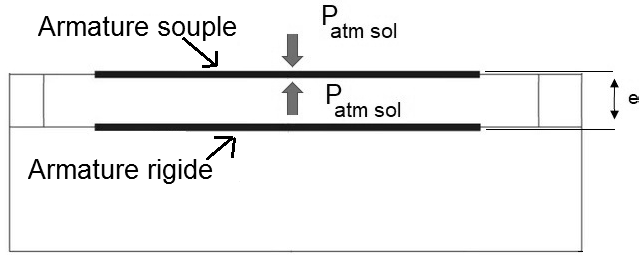
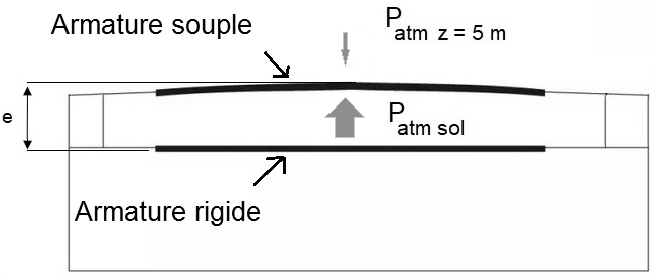
On rappelle que la capacité d’un condensateur plan constitué de deux plaques séparées par un isolant s’exprime par la relation :
$C=\frac{\epsilon S}{e} $
- C : capacité du condensateur (F)
- ε : permittivité diélectrique de l’isolant (F ∙ m–1)
- S : surface en regard de chaque armature (m2)
- e : distance entre les deux plaques (m)
D.5. Expliquer comment évolue la capacité C du condensateur lorsque le drone s’éloigne du sol. On supposera que la surface des armatures reste constante.
$$C=\frac{\varepsilon S}{e}$$
Quand le drone s’éloigne du sol, $e$ augmente, donc $C$ diminue.
D.6. Estimer la valeur de la capacité C du condensateur à 5,0 m du sol sachant que la variation de pression par rapport au sol provoque une augmentation de l’épaisseur e de 10 %.
On rappelle que la capacité C0 du condensateur au niveau du sol est égale à 100 μF.
$$\frac{C}{C_0}=\frac{\varepsilon S/e}{\varepsilon S/e_0}=\frac{e_0}{e}$$
Si $e=e_0\left(1+\frac{10}{100}\right)$ alors
$$C=\frac{e_0}{e_0\left(1+\frac{10}{100}\right)},C_0=\frac{1}{1{,}10},C_0$$
Avec $C_0=100\ \mu\mathrm{F}$ :
$$C=90,9\ \mu\mathrm{F}$$
