Installation d’un panneau routier

Nouvelle Calédonie 2025 Sujet 2

Exercice 3 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ2NC1

EXERCICE III – INSTALLATION D’UN PANNEAU ROUTIER (5 points)

Source : d’après https://www.trafic.fr/0-signalisation-routiere-panneaux-renforces-leds.html

Cet exercice étudie divers aspects d’un panneau routier lumineux, de type A13a (danger « endroit fréquenté par les enfants »), qui a été installé à proximité d’un groupe scolaire. Il est alimenté par un panneau solaire disposant d’une batterie de stockage d’énergie et d’un radar de vitesse.

Données :

• Constante de Planck : h = 6,63 × 10^–34 J·s.
• 1 eV = 1,60 × 10^–19 J.
• Célérité de la lumière : c = 3,00 × 10⁸ m·s^–1.
• Masse de l’électron : m_e = 9,11 × 10^–31 kg.
• Puissance lumineuse du Soleil, atteignant la surface de la Terre par un ciel clair, par unité de surface : Ps = 1000 W·m^–2.
• Valeur de la vitesse limite dans la zone de danger : vl_im = 30 km·h^–1.
• L’émetteur émet une onde électromagnétique de fréquence : f_E = 24,125 GHz.
• Le décalage Δf en fréquence est donné par la relation (avec v la valeur de la vitesse du véhicule détecté) :

$$|\Delta f|=2 \times f_E \times \frac{v}{c}$$

Partie A – Étude du panneau solaire

Le panneau de signalisation est alimenté par un ensemble de cellules photovoltaïques. Ces dernières sont constituées de silicium, un matériau semi-conducteur dont la bande de valence et la bande de conduction sont séparées par un travail d’extraction noté E_gap (figure 1).

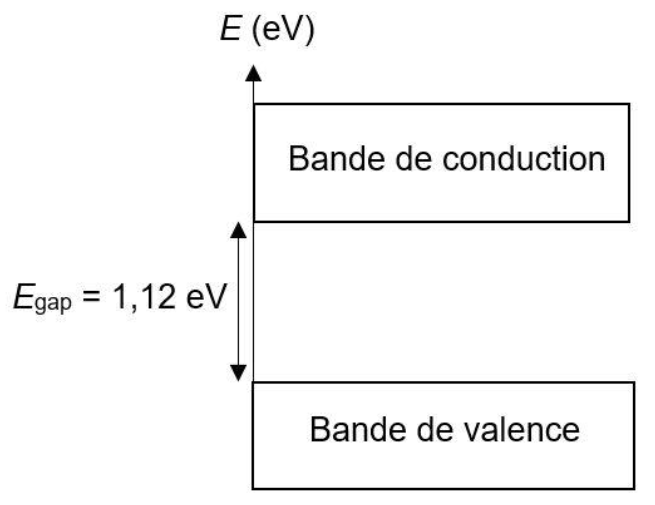
Figure 1 – Diagramme d’énergie du silicium

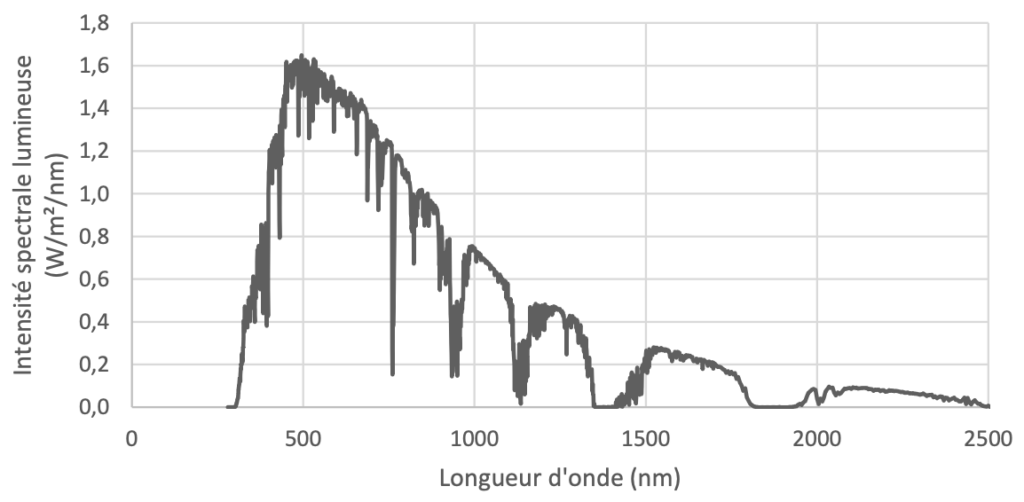
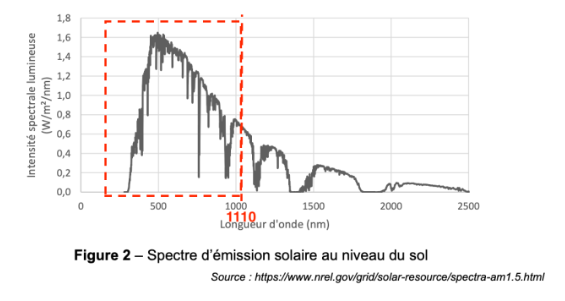
Figure 2 – Spectre d’émission solaire au niveau du sol

Source : https://www.nrel.gov/grid/solar-resource/spectra-am1.5.html

1. Décrire l’effet photoélectrique mis en jeu lors du fonctionnement de la cellule photovoltaïque.

L’effet photoélectrique est l’absorption de photons solaires par le silicium, permettant à des électrons de franchir la bande $E_{\mathrm{gap}}$ : ils passent de la bande de valence à la bande de conduction. Ce passage est à l’origine du courant électrique produit par le panneau solaire.

2. Citer une autre application de ce phénomène.

Une autre application de l’effet photoélectrique est le capteur photoélectrique utilisé dans les systèmes de détection de présence.

3. Calculer la longueur d’onde correspondante λ_seuil nécessaire à l’électron pour franchir le gap d’énergie.

$$E=\frac{h\times c}{\lambda}$$
$$E\times \lambda=h\times c$$
$$\lambda=\frac{h\times c}{E}$$
$$\lambda_{seuil}=\frac{h\times c}{E_{gap}}$$
$$\lambda_{seuil}=\frac{6,63\times {10}^{-34}\times 3,00\times {10}^8}{1,12\times 1,60\times {10}^{-19}}$$
$$\lambda_{seuil}=1,11\times {10}^{-6}\ m$$

4. Indiquer, en vous aidant de la figure 2, si l’utilisation de silicium est adaptée pour une cellule photovoltaïque.

Le panneau photovoltaïque, constitué d’une multitude de cellules, a les caractéristiques techniques suivantes :

Tension électrique Umax, à la puissance maximale	23,76 V
Intensité du courant électrique Imax, à la puissance maximale	0,89 A
Rendement	12 %
Dimensions du panneau (longueur × largeur × épaisseur)	795 × 220 × 25 (en mm)

Source : fiche technique https://www.jade-technologie.com/produits/panneaux-solaires-photovoltaique-verre-tedlar

5. Donner l’expression littérale du rendement du panneau photovoltaïque.

Leur rendement du panneau photovoltaïque est :
$$r=\frac{P_{electrique\ fournie}}{P_{lumineuse\ recue}}$$

6. Vérifier que la valeur du rendement du panneau photovoltaïque est bien celle indiquée par le fabricant.

$$r=\frac{P_{electrique\ fournie}}{P_{lumineuse\ recue}}$$

avec :
$$P_{electrique\ fournie}=U\times I$$

$$P_{lumineuse\ recue}=P_s\times S$$

D’ou
$$r=\frac{U\times I}{P_s\times S}$$
Or
$$S=L\times l$$

D’ou
$$r=\frac{U\times I}{P_s\times L\times l}$$
$$r=\frac{23,76\times 0,89}{1000\times 795\times {10}^{-3}\times 220\times {10}^{-3}}$$
$$r=0,12$$
$$r=12%$$

Ainsi, la valeur du rendement du panneau photovoltaïque est bien celle indiquée par le fabricant.

Partie B – Cinémomètre

Le panneau de signalisation est doté d’un radar de détection. Il s’agit d’un cinémomètre qui mesure la valeur de la vitesse du véhicule qui s’approche du panneau et déclenche son allumage en fonction d’une vitesse seuil. Si la valeur de la vitesse du véhicule est supérieure à la vitesse seuil, les LED du panneau routier s’allument et clignotent. Le panneau est installé en amont d’une zone dont la valeur de la vitesse limite est 30 km·h^–1. La valeur de la vitesse seuil a été fixée à 25 km·h^–1.

Le radar est constitué d’un émetteur et d’un récepteur d’ondes électromagnétiques de célérité c. Un analyseur permet de mesurer la différence de fréquence Δf entre l’onde émise et l’onde reçue si un obstacle en mouvement se présente face au radar. Cette analyse permet ensuite d’obtenir la valeur de la vitesse v du véhicule détecté.

7. Nommer et décrire le principe physique sur lequel repose le fonctionnement du radar.

Le fonctionnement du radar repose sur l’effet Doppler.

Le radar émet une onde électromagnétique de fréquence f_E en direction du véhicule. Cette onde est réfléchie par le véhicule en mouvement et revient vers le récepteur du radar.
La fréquence de l’onde reçue f_R est différente de celle de l’onde émise : on observe un décalage Doppler
La mesure de ce décalage de fréquence permet de calculer la vitesse du véhicule.

Un véhicule s’approche de l’école. Lors du passage de ce véhicule, la différence de fréquence mesurée entre l’onde émise et l’onde reçue est |Δf| = 2010 Hz.

8. Indiquer, en justifiant, si la fréquence du signal reçu est inférieure, égale ou supérieure à celle du signal émis.

Si le véhicule s’approche, la fréquence reçue est plus grande que la fréquence émise.
Si le véhicule s’éloigne, la fréquence reçue est plus petite
Dans notre cas, le véhicule s’approche de l’école : la fréquence reçue est supérieure à la fréquence du signal émis.

9. Déterminer si le panneau routier s’éclaire ou non, lors du passage du véhicule.

D’après le sujet : « Si la valeur de la vitesse du véhicule est supérieure à la vitesse seuil, les LED du panneau routier s’allument et clignotent. Le panneau est installé en amont d’une zone dont la valeur de la vitesse limite est 30 km·h^–1. La valeur de la vitesse seuil a été fixée à 25 km·h^–1. »

Calculons la valeur de la vitesse du véhicule :
$$\Delta f=2\times f_E\times \frac{v}{c}$$
$$2\times f_E\times \frac{v}{c}=\Delta f$$
$$v=\Delta f\times \frac{c}{2\times f_E}$$
$$v=\frac{2010\times 3,00\times {10}^8}{2\times 24,125\times {10}^9}$$
$$v=12,5\ m.s^{-1}$$
$$v=12,5\times 3,6$$
$$v=45\ km.h^{-1}$$
La vitesse du véhicule 45 km·h^–1 dépasse la vitesse seuil 25 km·h^–1 fixée pour l’allumage des LED du panneau. Ainsi, le panneau routier s’éclaire lors du passage du véhicule.

Le panneau de signalisation est équipé d’une batterie pour stocker l’énergie fournie par le panneau photovoltaïque. La batterie utilisée a une capacité de 4000 mAh.

On suppose que l’intensité moyenne nécessaire pour que les LED du panneau routier s’allument et clignotent est I_moyenne = 0,79 A.

10. Déterminer la durée maximale de clignotement du panneau routier possible pendant la nuit. Commenter.

$$Q=I\times \Delta t$$
$$I\times \Delta t=Q$$
$$\Delta t=\frac{Q}{I}$$
$$\Delta t=\frac{4000\times 10^{-3}}{0,79}$$
$$t=5,1\ \mathrm{h}$$
Cette durée correspond à une valeur maximale théorique, obtenue en supposant une batterie entièrement chargée sans perte énergétique et une intensité constante.

En pratique, la durée réelle de clignotement sera plus courte mais les voitures ne passent pas en continue la nuit, le trafic est faible la nuit.
Ainsi, une autonomie permettant 5 heures de fonctionnement continu est certainement suffisante pour assurer la signalisation lumineuse pendant une grande partie de la nuit.