Jeu de billes et gravité

Métropole 2025 Sujet 2 Bis

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ2ME4

Sujet et corrigé

Exercice 2 – Jeu de billes et gravité (5 points)

Certains jeux de construction, comme les circuits à billes, exploitent la gravité pour faire chuter des billes métalliques. Ces circuits contiennent des tours de hauteurs différentes et des rails droits ou courbes pour guider le chemin de la bille.

Le but de cet exercice est d’étudier le mouvement de la bille lorsqu’elle roule le long d’un rail et de vérifier s’il est possible de déduire une estimation de l’intensité de la pesanteur au travers de ce jeu.

Le mouvement de la bille est étudié dans le référentiel terrestre supposé galiléen. À la date t = 0, la bille est lâchée sans vitesse initiale du point A situé en haut d’une tour de hauteur H. Elle roule ensuite sans glisser jusqu’au point B, en ligne droite le long d’un rail de longueur L.

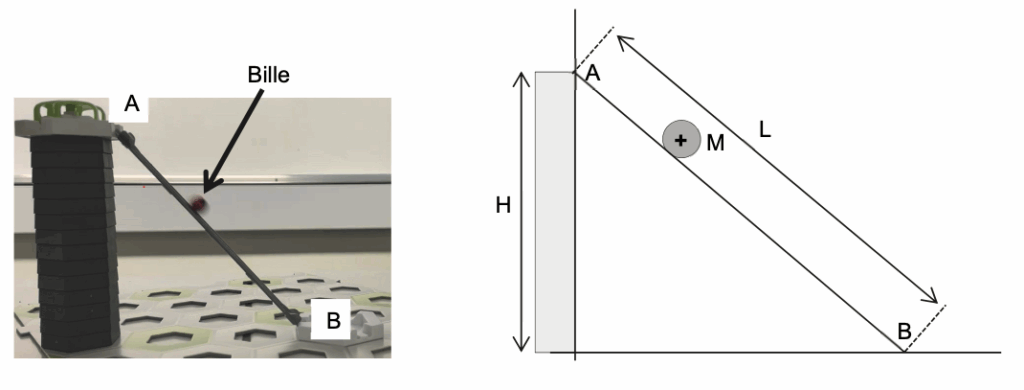
Figure 1. Photographie et schéma représentant la bille à un instant t sur le rail

Données :

• la bille est sphérique ;
• masse de la bille : m = 8,51 g ;
• volume de la bille : V = 1,07 cm³ ;
• masse volumique de différents métaux :

Métal	Acier	Cuivre	Aluminium
Masse volumique (kg·m–3)	ρacier= 7,9×103	ρcuivre= 9,0×103	ρaluminium= 2,7×103

• intensité de la pesanteur de référence : g_ref = 9,81 m·s^–2 ;
• la hauteur de la tour est notée H et la longueur du rail AB est notée L ;
• la référence d’énergie potentielle est choisie lorsque la bille est en contact avec le rail au point B ;
• pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\left|\frac{x – x_{\text{ref}}}{u(x)}\right|$ avec $x$ la valeur issue de la mesure, $x_{\text{ref}}$ la valeur de référence et $u(x)$ l’incertitude-type associée à la valeur mesurée $x$.

Q1. Déterminer la masse volumique ρ de la bille. En déduire la nature probable du matériau qui la constitue.

$\rho=\frac{m}{V}$
$\rho=\frac{8,51\times {10}^{-3}}{1,07\times {10}^{-6}}$
$\rho=7,95\times {10}^3\ Kg.m^{-3}$

La masse volumique trouvée est proche de celle de l’acier. Ainsi, la nature probable du matériau qui la constitue est l’acier.

On relève la position de la bille par chronophotographie. On détermine alors, par un traitement numérique, la valeur de la vitesse v de la bille à chaque instant, puis on représente graphiquement sur la figure 2 les évolutions au cours du temps de son énergie cinétique Ec, de son énergie potentielle Ep et de son énergie mécanique Em.

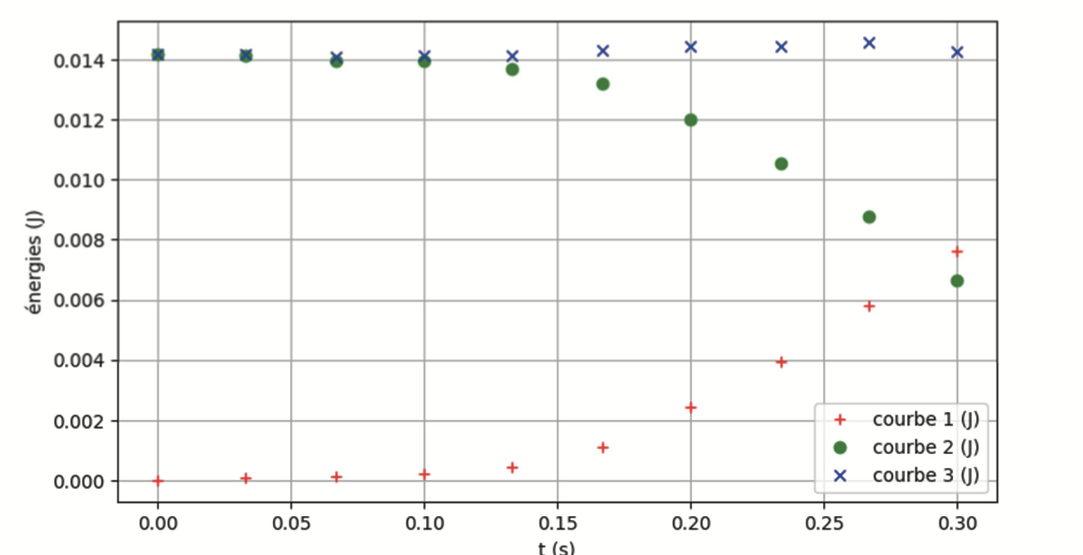
Figure 2. Représentation graphique de l’évolution des énergies potentielle, cinétique et mécanique de la bille au cours du temps

Q2. Identifier, parmi les courbes 1, 2 et 3, en justifiant, la courbe représentant l’évolution de l’énergie cinétique ainsi que celle représentant l’évolution de l’énergie potentielle de pesanteur sur la figure 2.

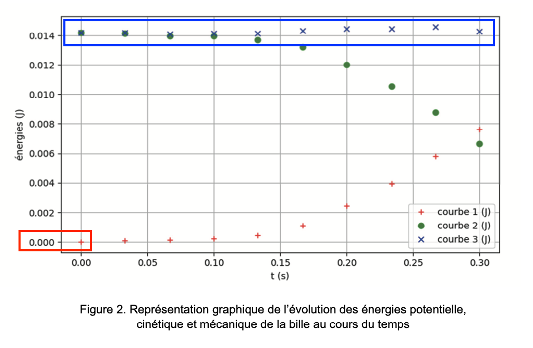
Q3. Décrire l’évolution temporelle de l’énergie mécanique de la bille à partir des données expérimentales. Commenter.

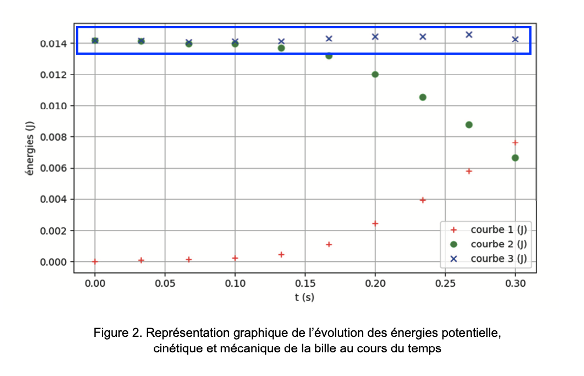
D’après l’énoncé : À la date t = 0, la bille est lâchée sans vitesse initiale du point A situé en haut d’une tour de hauteur H.
Calculons l’énergie cinétique à l’instant initial :
$E_c=\frac{1}{2}\times m\times v^2$
$E_c\left(0\right)=\frac{1}{2}\times m\times {v_0}^2$
$E_c\left(0\right)=\frac{1}{2}\times 8,51\times {10}^{-3}\times 0^2$
$E_c\left(0\right)=0\ J$
L’énergie cinétique initiale est nulle : Courbe 1

$E_{pp}=m\times g\times z$
$E_{pp}\left(0\right)=m\times g\times z_0$
$E_{pp}\left(0\right)=m\times g\times H$
L’énergie potentielle de pesanteur initiale n’est pas nulle (elle diminue au cours du temps car l’altitude z diminue) : Courbe 2

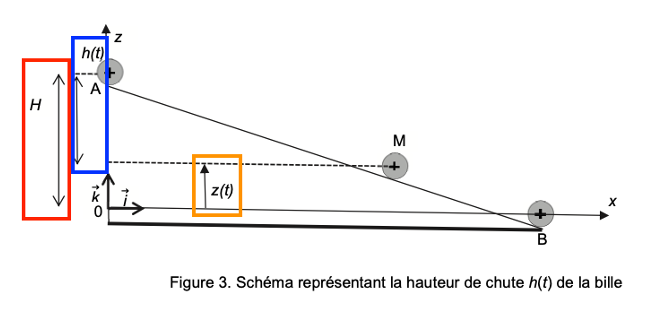
Les données précédentes ont été obtenues en étudiant le mouvement de la bille dans le repère d’espace (Ox ; Oz) muni des vecteurs unitaires $\vec{i}$ et $\vec{k}$ (voir figure 3). Les coordonnées du centre de masse sont notées x(t) et z(t). L’origine de l’énergie potentielle de pesanteur de la bille est prise lorsque son centre de masse est à la position z = 0.

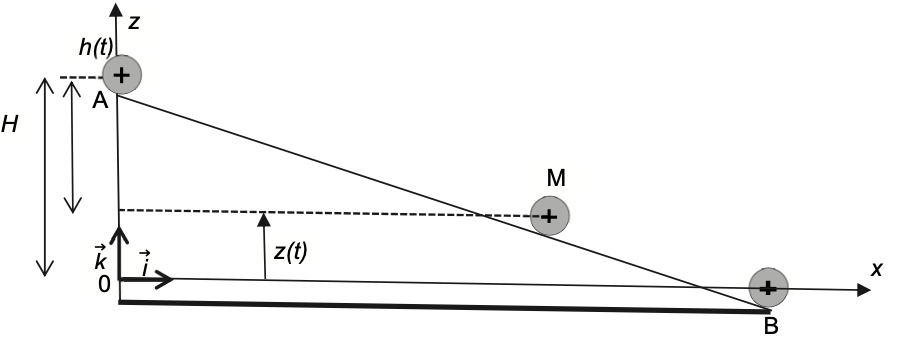
Figure 3. Schéma représentant la hauteur de chute h(t) de la bille

Un programme, écrit en langage Python, a permis d’obtenir les données précédentes. Deux extraits en sont donnés en figure 4.

Extrait 1 :

Extrait 2 :

Figure 4. Extraits du programme écrit en langage Python permettant de calculer les énergies potentielle, cinétique et mécanique au cours du temps

La variable N correspond ici au nombre d’images pointées sur la vidéo du mouvement de la bille allant du point A au point B.

La fonction range(a,b) renvoie les entiers de a à b-1 par pas de 1. Les valeurs des variables x, z et t sont stockées dans des tableaux x, z et t, indicés de 0 à N-1.

Q4. Expliquer pourquoi le programme présenté en figure 4 ne permet pas de calculer l’énergie cinétique aux points A et B.

    vx[i] = (x[i+1]-x[i-1])/(t[i+1]-t[i-1])

    vz[i] = (z[i+1]-z[i-1])/(t[i+1]-t[i-1])

A la ligne 76 le programme calcul vx et à la ligne 77 vy.

Pour calculer la vitesse en un point, le programme utilise le point d’après (i+1) et le point d’avant (i-1).

Le point A est le premier point : il n’y a pas de point avant, le programme ne permet pas de calculer la vitesse en A et donc l’énergie cinétique au point.

Le point B est le dernier point : il n’y a pas de point après, le programme ne permet pas de calculer la vitesse en B et donc l’énergie cinétique au point.

Ainsi, le programme ne permet pas de calculer l’énergie cinétique aux points A et B.

Q5. Recopier et compléter les lignes 81 et 84 du programme écrit en langage Python présenté en figure 4 afin qu’il calcule les énergies potentielle Ep et mécanique Em.

$E_{pp}=m\times g\times z$ :

81 Ep[i] = m*g*z[i]              # énergie potentielle de pesanteur

Em= Ep + Ec :

84 Em[i] = Ep[i] + Ec[i]         # énergie mécanique

Lors du mouvement étudié sur cette portion du circuit, la bille roule sans glisser. Son énergie cinétique, qui tient compte de la rotation de la bille sur elle-même, est exprimée par la relation suivante :

$$E_c = \frac{7}{10} \, m \, v^2$$

Q6. En appliquant la conservation de l’énergie mécanique entre l’instant initial t = 0 et l’instant t, montrer que l’expression de la vitesse de la bille à l’instant t s’écrit :

$$v(t) = \sqrt{\frac{10}{7} \, g \, h(t)}$$

avec h(t) la hauteur de chute, c’est-à-dire la différence d’altitude du centre de masse de la bille entre l’instant initial t = 0 et l’instant t.

D’après le sujet, l’énergie mécanique se conserve :
$E_m\left(t\right)=E_m(0)$
$E_c\left(t\right)+\ E_p\left(t\right)=E_c(0)+E_p(0)$
Dans cet exercice : $E_c=\frac{7}{10}\times m\times v^2$
$\frac{7}{10}\times m\times {v\left(t\right)}^2+m\times g\times z\left(t\right)=\frac{7}{10}\times m\times v_0^2+m\times g\times H$
$\frac{7}{10}\times m\times {v\left(t\right)}^2+m\times g\times z\left(t\right)=\frac{7}{10}\times m\times 0^2+m\times g\times H$
$\frac{7}{10}\times m\times {v\left(t\right)}^2+m\times g\times z\left(t\right)=m\times g\times H$
$\frac{7}{10}\times m\times {v\left(t\right)}^2=m\times g\times H-m\times g\times z\left(t\right)$
$\frac{7}{10}\times m\times {v\left(t\right)}^2=m\times g\times \left(H-z\left(t\right)\right)$
${v\left(t\right)}^2=\frac{10}{7}\times g\times \left(H-z\left(t\right)\right)$
$v\left(t\right)=\sqrt{\frac{10}{7}\times g\times \left(H-z\left(t\right)\right)}$

D’où
$v\left(t\right)=\sqrt{\frac{10}{7}\times g\times \left(H-\left(H-h\left(t\right)\right)\right)}$
$v\left(t\right)=\sqrt{\frac{10}{7}\times g\times \left(H-H+h\left(t\right)\right)}$
$v\left(t\right)=\sqrt{\frac{10}{7}\times g\times h\left(t\right)}$

L’évolution observée du carré de la vitesse en fonction de la hauteur de chute h(t) est représentée sur la figure 5. Les points expérimentaux sont modélisés par une droite d’équation :

v²(t) = k·h(t)

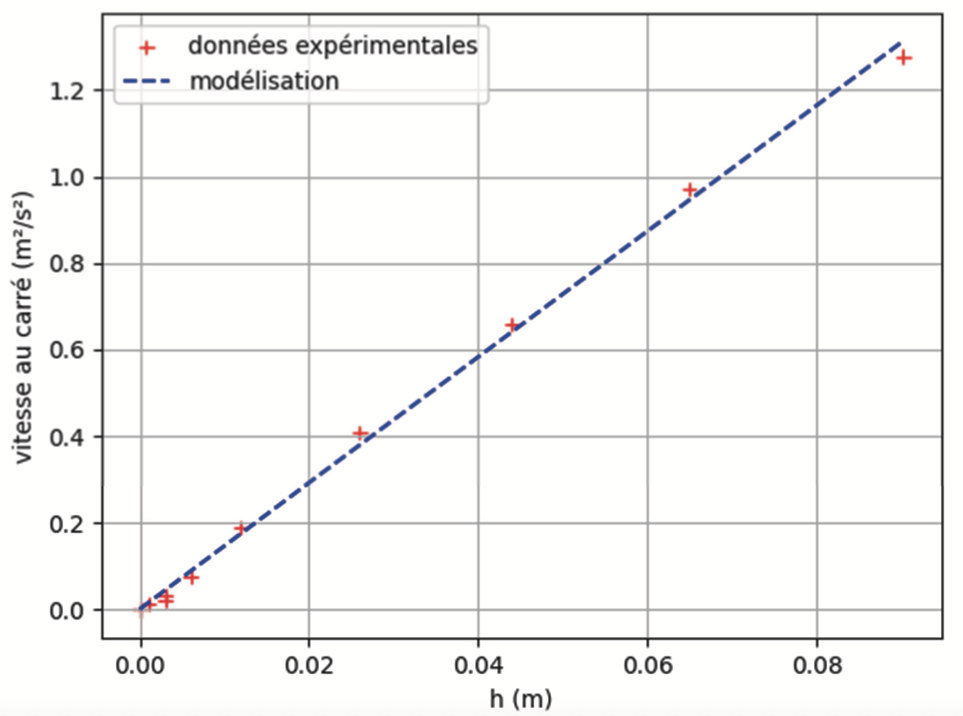
Figure 5. Évolution du carré de la vitesse v²(t) en fonction de la hauteur de chute h(t) de la bille au cours du temps

Q7. Justifier que l’équation de la modélisation de la figure 5 est cohérente avec l’expression donnée en Q6.

La modélisation de la figure 5 montre une droite passant par l’origine. La vitesse au carré est proportionnelle à la hauteur h :
${v\left(t\right)}^2=k\times h\left(t\right)$

Question 6 :
$v\left(t\right)=\sqrt{\frac{10}{7}\times g\times h\left(t\right)}$
${v\left(t\right)}^2=\frac{10}{7}\times g\times h\left(t\right)$
La vitesse au carré est proportionnelle à la hauteur h.

Ainsi, l’équation de la modélisation de la figure 5 est cohérente avec l’expression donnée en Q6.

Q8. Déterminer la relation entre l’intensité de la pesanteur g et la constante k. Calculer la valeur de l’intensité de la pesanteur g dans cette expérience, sachant que l’analyse des résultats reportés sur la figure 5 donne la valeur k = 14,53 m·s^–2.

${v\left(t\right)}^2=\frac{10}{7}\times g\times h\left(t\right)$
${v\left(t\right)}^2=k\times h\left(t\right)$
Par identification :
$k=\frac{10}{7}\times g$

Calculons la valeur de l’intensité de la pesanteur g dans cette expérience :
$k=\frac{10}{7}\times g$
$\frac{10}{7}\times g=k$
$g=k\times \frac{7}{10}$
$g=14,53\times \frac{7}{10}$
$g=10,17\ m.s^{-2}$

On reproduit sept fois la chute de la bille et on rassemble les valeurs de l’intensité de la pesanteur déterminées pour chacune des expériences dans le tableau suivant :

Expérience	1	2	3	4	5	6	7	8
Valeur expérimentale de l’intensité de la pesanteur g (m·s–2 )	10,17	9,70	9,81	10,19	10,32	10,32	9,42	9,89

Un traitement statistique des données du tableau précédent permet d’obtenir que l’incertitude-type sur la mesure de l’intensité moyenne de la pesanteur est u(g_moy) = 0,11 m·s^–2.

Q9. Discuter de l’accord du résultat de la mesure de l’intensité moyenne de la pesanteur issu des huit expériences avec sa valeur de référence. Conclure sur l’utilisation de cette méthode pour mesurer la valeur de l’intensité de la pesanteur avec ce jeu.

Calculons la moyenne des valeurs expérimentales de l’intensité de la pesanteur g :
$g_{moy}=\frac{10,17+9,70+9,81+10,19+10,32+10,32+9,42+9,89}{8}$
$g_{moy}=9,98\ m.s^{-2}$

Pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient |x – xref|/u(x) avec x la valeur issue de la mesure, xref la valeur de référence et u(x) l’incertitude-type associée à la valeur mesurée x.

$z=\left|\frac{g-g_{ref}}{u\left(g\right)}\right|$
$z=\left|\frac{9,98-9,81}{0,11}\right|$
$z=1,5$
$z<2$ : le résultat de la mesure est compatible avec la valeur de référence $g_{moy}=9,81\ m.s^{-2}$.

Ainsi, l’utilisation de cette méthode pour mesurer la valeur de l’intensité de la pesanteur avec ce jeu est valable.