Métropole Septembre 2025 Sujet 2
Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°25-PYCJ2ME3
Sujet et corrigé
Exercice 2 – La couleur des scarabées (5 points)
Les scarabées ont des carapaces constituées de nanostructures. Ces dernières, lorsqu’elles sont éclairées, créent des interférences lumineuses qui donnent à ces insectes des couleurs variées. Dans cet exercice, on se propose d’étudier ce phénomène.
La partie supérieure du squelette externe d’un scarabée est représentée sur la figure 1. Elle est constituée d’un empilement de couches transparentes de quelques dizaines de nanomètres d’épaisseur chacune, ayant alternativement un fort indice optique et un faible indice optique comme le montre la figure 2.

Figure 1. Schéma du squelette externe du scarabée
D’après passion-entomologie.fr
Quand le scarabée est éclairé en lumière blanche, chacune des radiations monochromatiques composant la lumière blanche se réfléchit à chaque interface entre deux couches de la partie supérieure du squelette. Les radiations réfléchies se superposent alors au niveau de l’œil de l’observateur, interfèrent entre elles et sont ainsi à l’origine de la couleur perçue du scarabée.
On simplifie l’étude de la façon suivante (voir figure 2) :
- on ne prend en compte que l’interférence entre les deux premiers rayons réfléchis 1 et 2 ;
- toutes les couches sont supposées de même épaisseur, notée e.

Figure 2. Schéma simplifié de la situation
Données :
- indice optique de la couche d’indice le plus fort : nfort = 1,7 ;
- pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\dfrac{|x – x_{\text{ref}}|}{u(x)}$ avec x la valeur mesurée, $x_{\text{ref}}$ la valeur de référence et $u(x)$ l’incertitude-type associée à la valeur mesurée x ;
- couleur observée associée à une radiation de longueur d’onde λ :
| Longueur d’onde λ (en nm) | 470 | 530 | 590 | 750 |
| Couleur | bleu | vert | jaune | rouge |
Q1. Rappeler la condition d’obtention d’interférences constructives entre deux ondes, issues d’une source monochromatique unique, ayant parcouru des chemins optiques différents. On note δ la différence de chemin optique et λ la longueur d’onde.
On observe des interférences constructives quand $\delta=k\times \lambda$ : les ondes sont en phase
On observe des interférences destructives quand $\delta=\left(k+\frac{1}{2}\right)\times \lambda$ : les ondes sont en opposition de phase
Dans cet exercice on admet que la lumière incidente se propage dans une direction perpendiculaire à la surface du squelette externe. Pour une onde monochromatique de longueur d’onde λ, la différence de chemin optique δ au niveau de l’œil de l’observateur entre les radiations réfléchies 1 et 2 est donnée par la relation suivante :
$$\delta = 2 \cdot n_{fort} \cdot e – \frac{\lambda}{2}$$
Q2. Montrer que les épaisseurs correspondant à des interférences constructives sont données par la relation suivante dans laquelle k est un nombre entier positif ou nul, appelé ordre d’interférence :
$$e = \left( k + \frac{1}{2} \right) \times \frac{\lambda}{2 \cdot n_{fort}}$$
D’après l’énoncé :
$$\delta=2\cdot n_{fort}\cdot e-\frac{\lambda}{2}$$
$$2\cdot n_{fort}\cdot e-\frac{\lambda}{2}=\delta$$
$$2\cdot n_{fort}\cdot e=\delta+\frac{\lambda}{2}$$
$$e=\frac{\delta+\frac{\lambda}{2}}{2\cdot n_{fort}}$$
Or nous sommes dans un cas d’interférences constructives :
$$\delta=k\times \lambda$$
D’où
$$e=\frac{k\times \lambda+\frac{\lambda}{2}}{2\cdot n_{fort}}$$
$$e=\frac{\left(k+\frac{1}{2}\right)\times \lambda}{2\cdot n_{fort}}$$
On obtient bien :
$$e=\left(k+\frac{1}{2}\right)\times \frac{\lambda}{2\cdot n_{fort}}$$
Le scarabée est éclairé en lumière blanche. Dans la lumière réfléchie, les ondes lumineuses donnant lieu à des interférences constructives voient leur intensité renforcée. La lumière réfléchie apparait donc colorée.
On ne considère, dans la suite de l’exercice, que l’ordre d’interférence nul : k = 0.
Q3. Déterminer l’épaisseur des couches de la carapace d’un scarabée pour lequel la longueur λ = 530 nm correspond à des interférences constructives. Préciser la couleur apparente de ce scarabée.
Déterminons l’épaisseur des couches de la carapace d’un scarabée pour lequel la longueur $\lambda = 530\ \text{nm}$ correspond à des interférences constructives avec l’ordre d’interférence nul : $k = 0$.
$$e=\left(k+\frac{1}{2}\right)\times \frac{\lambda}{2\cdot n_{fort}}$$
$$e=\left(0+\frac{1}{2}\right)\times \frac{530\times {10}^{-9}}{2\times 1,7}$$
$$e=7,8\times {10}^{-8}\ m$$
$$e=78\ nm$$
D’après l’énoncé la longueur $\lambda = 530\ \text{nm}$ correspond au vert. Ainsi, la couleur apparente de ce scarabée est verte.

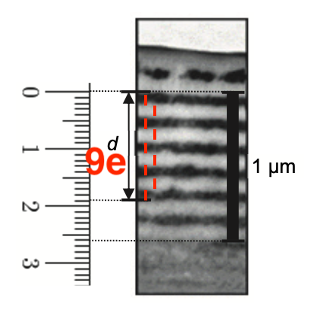
On souhaite comparer l’épaisseur trouvée précédemment avec une mesure directe sur une photo, prise au microscope électronique, de la partie supérieure du squelette du scarabée.

La photographie ci-contre, prise au microscope électronique, montre l’alternance des couches de fort indice optique (en noir) et de faible indice optique (en gris clair) dans la partie supérieure du squelette d’un scarabée vert.
L’échelle de la photographie est indiquée grâce à la barre verticale noire située à droite : cette barre indique une longueur de 1 µm.
Une règle, graduée en cm, est représentée à gauche de la photographie pour effectuer toute mesure utile.
Figure 3. Photographie prise au microscope électronique de la partie supérieure d’un scarabée vert D’après Bioinspiration Biomimetics (2013)
Q4. À partir de la figure 3, déterminer la valeur de l’épaisseur moyenne e d’une couche. Expliciter la méthode suivie pour obtenir la meilleure précision possible sur la mesure de e. La distance d indiquée sur la figure 3 peut servir d’aide à la mesure.
| Schéma | Réel |
| 2,6 cm | 1 μm |
| 1,9 cm | d=9e |
$$9e=\frac{1,9\times 1}{2,6}$$
$$9e=0,73\ \mu m$$
$$e=\frac{0,73}{9}$$
$$e=0,081\ \mu m$$
$$e=0,081\times {10}^{-6}$$
$$e=8,1\times {10}^{-8}\ m$$
Q5. Indiquer une source d’incertitude possible dans la détermination de la mesure de l’épaisseur e effectuée à la question Q4.
Une source d’incertitude possible est la lecture des épaisseurs sur la photo (frontières difficilement définies).
On souhaite maintenant évaluer quantitativement la précision de cette mesure à l’aide d’une simulation numérique.
La valeur de la distance d estimée sur la photographie se situe dans un intervalle de valeurs exprimées en cm. Un programme écrit en langage Python permet de calculer l’épaisseur d’une couche pour 5 000 longueurs prises aléatoirement dans cet intervalle de valeurs.
Un extrait du programme est représenté ci-dessous, dans lequel la fonction rd.uniform(a,b,Nsim) permet de renvoyer Nsim valeurs aléatoires comprises entre les valeurs a et b.
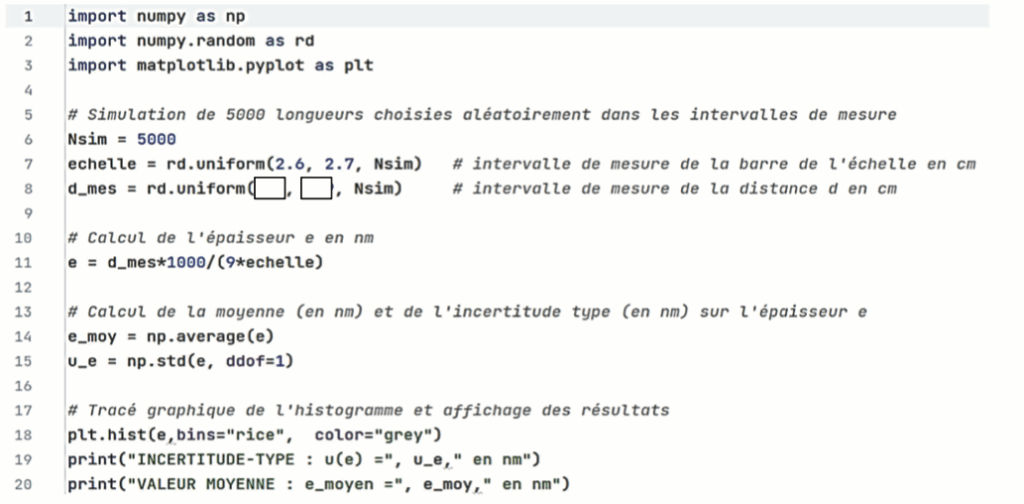
Figure 4. Extrait du programme Python
Le programme permet de calculer la valeur moyenne et l’incertitude-type u(e) sur une mesure de e puis d’afficher :
INCERTITUDE-TYPE : u(e) = 2.5574799015216696 en nm
VALEUR MOYENNE : e_moyen = 75.48793757378112 en nm
Q6. Recopier la ligne 8 du programme puis la compléter avec des valeurs appropriées exprimées en cm.
La ligne 8 donne l’intervalle de mesure de la distance d en cm
Dans la question précédente (Q4), on a mesuré la distance d=1,9 cm sur la règle avec une incertitude de lecture d’environ ±0,1 cm correspondant à une graduation.
L’intervalle est donc : 1,9 cm ±0,1 cm soit [1,8 ; 2,0] cm.
Donc la ligne 8 du programme devient :
d_mes = rd.uniform(1.8, 2.0, Nsim) # intervalle de mesure de la distance d en cm
Q7. Justifier la présence du nombre 1 000 dans l’expression de la ligne 11 du programme de la figure 4.
L’expression ligne 11 est :
$$e=\frac{d_{\mathrm{mes}}\times 1000}{9\times \mathrm{echelle}}$$
À la ligne 10 on nous précise « calcul de l’épaisseur e en nm ».
Le facteur 1000 permet de convertir l’épaisseur exprimée initialement en µm en nm :
1 µm = 1000 nm.
Q8. En utilisant les résultats de la simulation numérique et en conservant un seul chiffre significatif pour l’incertitude-type, écrire le résultat de la mesure de l’épaisseur emoyen. Discuter la compatibilité de la réponse à la question Q3, arbitrairement prise comme valeur de référence, avec le résultat de la simulation numérique.
INCERTITUDE-TYPE : u(e) = 2.5574799015216696 en nm
VALEUR MOYENNE : e_moyen = 75.48793757378112 en nm
On ne garde qu’un seul chiffre significatif pour l’incertitude et on majore le résultat : u(e) = 3 nm.
L’incertitude porte sur les unités.
Pour la valeur moyenne, on garde le résultat à l’unité en arrondissant : emoyen = 75 nm
Ainsi :
e_moyen = 75 ± 3 nm
Pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\left|\frac{x-x_{ref}}{u\left(x\right)}\right|$ avec x la valeur mesurée, xref la valeur de référence et u(x) l’incertitude-type associée à la valeur mesurée x ;
Calculons le z-score :
$$z=\left|\frac{x-x_{ref}}{u\left(x\right)}\right|$$
$$z=\left|\frac{e_{moyen}-e}{u\left(e\right)}\right|$$
$$z=\left|\frac{75-78}{3}\right|$$
$$z=1$$
z<2 : le résultat de la réponse à la question Q3, arbitrairement prise comme valeur de référence est avec le résultat de la simulation numérique.
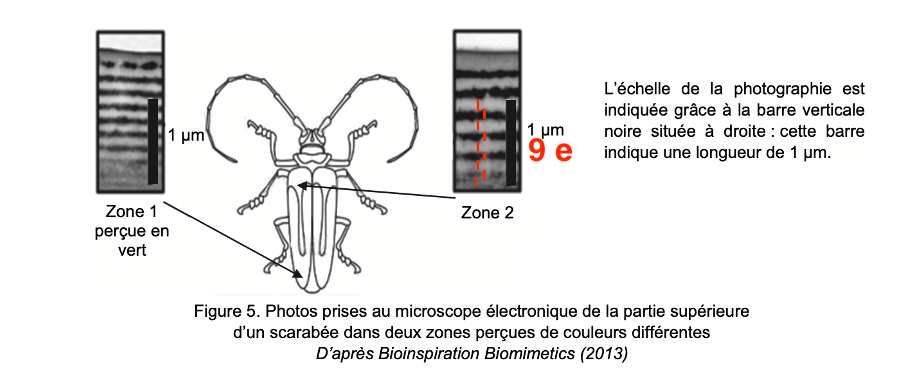
Certains scarabées possèdent des carapaces bicolores. La figure 5 représente les photos prises au microscope électronique de la partie supérieure du squelette externe du scarabée pour deux zones d’épaisseurs et de couleurs différentes. La zone 1 est de couleur verte. Les deux photos sont à la même échelle.
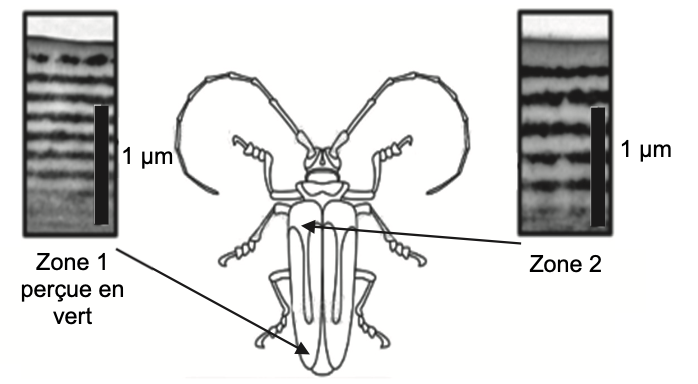
L’échelle de la photographie est indiquée grâce à la barre verticale noire située à droite : cette barre indique une longueur de 1 µm.
Figure 5. Photos prises au microscope électronique de la partie supérieure d’un scarabée dans deux zones perçues de couleurs différentes
D’après Bioinspiration Biomimetics (2013)
Q9. Estimer la longueur d’onde qui correspond à des interférences constructives dans la zone 2. Proposer une hypothèse pour la couleur perçue pour la zone 2 de ce scarabée.
Le candidat est invité à prendre des initiatives et à présenter sa démarche même si elle n’a pas abouti. La démarche suivie est évaluée et nécessite donc d’être correctement présentée.
$$9e=1\ \mu m$$
$$e=\frac{1\times 1}{9}$$
$$e=0,11\ \mu m$$
$$e=0,11\times {10}^{-6}$$
$$e=1,1\times {10}^{-7}\ m$$
D’après la question Q2 :
$$e=\left(k+\frac{1}{2}\right)\times \frac{\lambda}{2\cdot n_{fort}}$$
$$\left(k+\frac{1}{2}\right)\times \frac{\lambda}{2\cdot n_{fort}}=e$$
$$\lambda=\frac{e\times 2\cdot n_{fort}}{k+\frac{1}{2}}$$
D’après l’énoncé (juste avant la question Q3) : « On ne considère, dans la suite de l’exercice, que l’ordre d’interférence nul : k = 0. »
$$\lambda=\frac{1,1\times {10}^{-7}\times 2\times 1,7}{0+\frac{1}{2}}$$
$$\lambda=7,5\times {10}^{-7}m$$
$$\lambda=750\ nm$$
Ainsi, la couleur perçue pour la zone 2 de ce scarabée est le rouge.

