La découverte de Neptune

Bac Métropole Septembre 2024 Sujet 1

Exercice 2 – (5 points) – Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ1ME3

Exercice 2 – La découverte de Neptune (5 points)

Suite à la découverte de la planète Uranus en 1781 et à l’étude de sa trajectoire, certains astronomes supposèrent l’existence d’une autre planète qui influencerait son mouvement. En 1846, le français Urbain Le Verrier parvint à proposer, par le calcul, des caractéristiques de cette nouvelle planète. Grâce aux indications de Le Verrier et à l’aide de la lunette astronomique de l’observatoire de Berlin, l’astronome Johann Galle repéra dès ses premières nuits d’observation le nouvel astre qui porte depuis le nom de Neptune.

Le but de cet exercice est d’analyser certaines prévisions de Le Verrier puis d’étudier l’observation de Neptune avec la lunette astronomique de l’observatoire de Berlin.

1. Les caractéristiques de Neptune selon les prévisions de Le Verrier Données :

conversion d’une distance exprimée en mètre (m) en une distance exprimée en unité astronomique (UA) : 1 UA = 1,50×10¹¹ m ;
valeurs de référence actuellement admises pour quelques paramètres planétaires :
- demi-grand axe l’orbite de la planète Uranus : a_{Réf U} = 19,2 UA ;
- période de révolution de la planète Uranus autour du Soleil : T_{Réf U} = 84,1 ans ;
- période de révolution de la planète Neptune autour du Soleil : T_{Réf N} = 165 ans ;
la planète Neptune est plus éloignée du Soleil que la planète Uranus ;
pour discuter de l’accord du résultat d’une mesure avec une valeur de référence, on peut utiliser le quotient $\frac{\left|x-x_{\text{ref}}\right|}{u(x)}$ avec x la valeur mesurée, x_ref la valeur de référence et u(x) l’incertitude-type associée à la valeur mesurée x.

Sur la figure 1 ci-dessous, ont été représentés l’orbite elliptique d’une planète autour du Soleil ainsi que le demi-grand axe a de cette orbite.

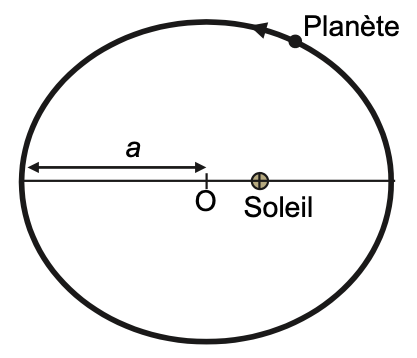
Figure 1. Orbite elliptique, de demi-grand axe a, d’une planète autour du Soleil

Q1. Nommer la position particulière occupée par le Soleil pour l’ellipse représentée en figure 1. Préciser le nom de l’astronome connu pour avoir établi ce résultat.

La position particulière occupée par le Soleil pour l’ellipse représentée en figure 1 est un des foyers de l’ellipse.
L’astronome connu pour avoir établi ce résultat est Johannes Kepler.

On peut montrer que pour tous les objets en orbite elliptique autour du Soleil, le rapport $\frac{T^2}{a^3}$ entre le carré de la période de révolution T et le cube du demi-grand axe a de l’orbite est le même.

Q2. Justifier que la période de révolution de Neptune est plus grande que celle d’Uranus.

Pour tous les objets en orbite elliptique autour du Soleil, le rapport $\frac{T^2}{a^3}$ est le même.
Ainsi :
$\frac{T_{Neptune}^2}{a_{Neptune}^3}=\frac{T_{Uranus}^2}{a_{Uranus}^3}$
$T_{Neptune}^2=a_{Neptune}^3\times\frac{T_{Uranus}^2}{a_{Uranus}^3}$
$T_{Neptune}^2=\frac{a_{Neptune}^3}{a_{Uranus}^3}\times T_{Uranus}^2$
$T_{Neptune}^2=\left(\frac{a_{Neptune}}{a_{Uranus}}\right)^3\times T_{Uranus}^2$

D’après les données : la planète Neptune est plus éloignée du Soleil que la planète Uranus
$a_{Neptune}>a_{Uranus}$
$\frac{a_{Neptune}}{a_{Uranus}}>1$
$\left(\frac{a_{Neptune}}{a_{Uranus}}\right)^3>1$
Donc
$T_{Neptune}^2>T_{Uranus}^2$
$T_{Neptune}>T_{Uranus}$

Ainsi, la période de révolution de Neptune est plus grande que celle d’Uranus.

Dans son mémoire présenté en 1846, Le Verrier indique que, selon ses calculs, Neptune a une orbite elliptique de demi-grand axe aVerrier N = 36,2 UA.

Q3. Déterminer à l’aide de a_{Réf U}, T_{Réf U} et a_{Verrier N}, la valeur en années de la période de révolution T_{Verrier N}de la planète Neptune pour l’orbite prévue par Le Verrier.

$\frac{T_{Neptune}^2}{a_{Neptune}^3}=\frac{T_{Uranus}^2}{a_{Uranus}^3}$
$T_{Neptune}^2=a_{Neptune}^3\times\frac{T_{Uranus}^2}{a_{Uranus}^3}$
$T_{Neptune}^2=\frac{a_{Neptune}^3}{a_{Uranus}^3}\times T_{Uranus}^2$
$T_{Neptune}^2=\left(\frac{a_{Neptune}}{a_{Uranus}}\right)^3\times T_{Uranus}^2$
$T_{Neptune}=\sqrt{\left(\frac{a_{Neptune}}{a_{Uranus}}\right)^3\times T_{Uranus}^2}$
$T_{Neptune}=\sqrt{\left(\frac{a_{Neptune}}{a_{Uranus}}\right)^3}\times T_{Uranus}$

$T_{Verrier\ N}=\sqrt{\left(\frac{a_{Verrier\ N}}{a_{Ref\ U}}\right)^3}\times T_{Ref\ U}$
$T_{Verrier\ N}=\sqrt{\left(\frac{36,2}{19,2}\right)^3}\times 84,1$
$T_{Verrier\ N}=218\ ans$

Grâce au mémoire de Le Verrier, il est possible d’estimer l’incertitude-type u(T_{Verrier N}) associée à la valeur T_{Verrier N} obtenue en Q3 : u(T_{Verrier N}) = 13 ans.

Q4. Discuter de l’accord du résultat de T_{Verrier N} avec la valeur de référence actuelle T_{Réf N}.

Calculons le quotient $\frac{\left|T_{Verrier\ N}-T_{Ref\ N}\right|}{u\left(T_{Verrier\ N}\right)}$ :
$\frac{\left|T_{Verrier\ N}-T_{Ref\ N}\right|}{u\left(T_{Verrier\ N}\right)}=\frac{\left|218-165\right|}{13}=4>2$

Le quotient $\frac{\left|T_{Verrier\ N}-T_{Ref\ N}\right|}{u\left(T_{Verrier\ N}\right)}$ est supérieur à 2 : le résultat de T_{Verrier N}n’est pas en accord avec la valeur de référence actuelle T_{Réf N}.

Le Verrier a mené ses calculs en étudiant les perturbations exercées par Uranus sur Neptune. L’orbite d’Uranus n’était pas encore décrite avec précision au début du XIXe siècle. Le Verrier a donc été contraint à plusieurs approximations, ce qui explique la différence obtenue sur la trajectoire calculée pour Neptune comme en témoigne la figure 2.

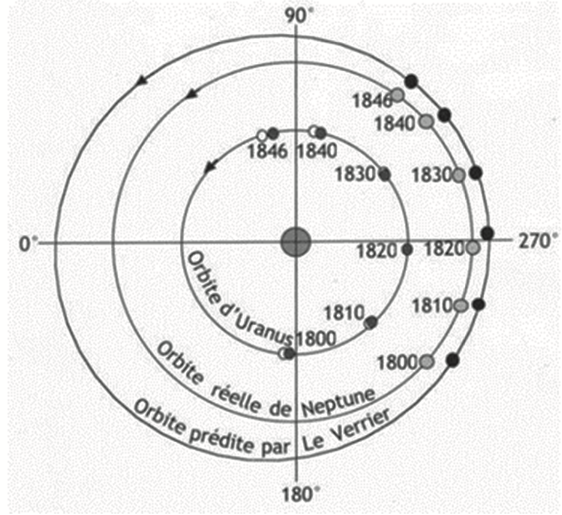
Figure 2. Orbites d’Uranus et de Neptune (le schéma n’est pas à l’échelle)
D’après La découverte de Neptune par Le Verrier (1846), James Lequeux

Q5. À l’aide de la figure 2, comparer de manière qualitative la valeur du demi-grand axe de l’orbite prédite par Le Verrier avec la valeur du demi-grand axe de l’orbite réelle de Neptune. Montrer la cohérence de la réponse avec les résultats de la question Q3.

La figure 2 nous montre que la valeur du demi-grand axe de l’orbite prédite par Le Verrier est supérieure à la valeur du demi-grand axe de l’orbite réelle de Neptune.
$T_{Verrier\ N}=\sqrt{\left(\frac{a_{Verrier\ N}}{a_{Ref\ U}}\right)^3}\times T_{Ref\ U}$
T_{Verrier N}est proportionnel à la racine carrée du cube du demi-grand axe a_{Verrier N}.
En surestiment la valeur du cube du demi-grand axe a_{Verrier N}, il obtient T_{Verrier N} supérieure à la valeur réelle.
T_{Verrier N}=218 ans > T_{Ref N}=165 ans
C’est cohérent avec la réponse avec les résultats de la question Q3.

2. Observation de Neptune

Données :

distance entre Neptune et la Terre en août 1846 : d_T–N = 4,4×10⁹ km ;
diamètre de Neptune : D = 4,95×10⁴ km ;
pouvoir séparateur de l’œil : on peut distinguer deux points différents d’un astre si l’angle sous lequel on voit ces deux points depuis la Terre est supérieur ou égal à 3×10^–4 rad environ ;
approximation dans le cas de petits angles (θ << 1 rad : tan θ = θ).

L’observation de Neptune par Galle avec la lunette astronomique de l’observatoire de Berlin a été réalisée en août 1846. On note θ l’angle sous lequel Neptune a pu être vue à l’œil nu depuis la Terre à la fin de l’été 1846.

Q6. À l’aide des données, montrer que la valeur de l’angle θ est voisine de 1,1×10^–5 rad.

Pour des petits angles, exprimés en radian : tan 𝜃 ≈ 𝜃
$\theta\approx \tan\ \theta=\frac{oppose}{adjacent}$
$\theta=\frac{D}{d_{T-N}}$
$\theta=\frac{4,95\times {10}^4}{4,4\times {10}^9}$
$\theta=1,1\times {10}^{-5}\ rad$

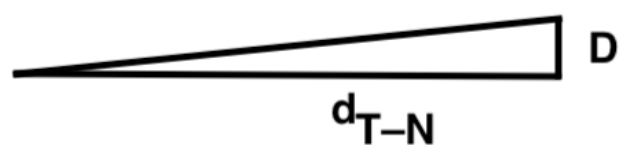
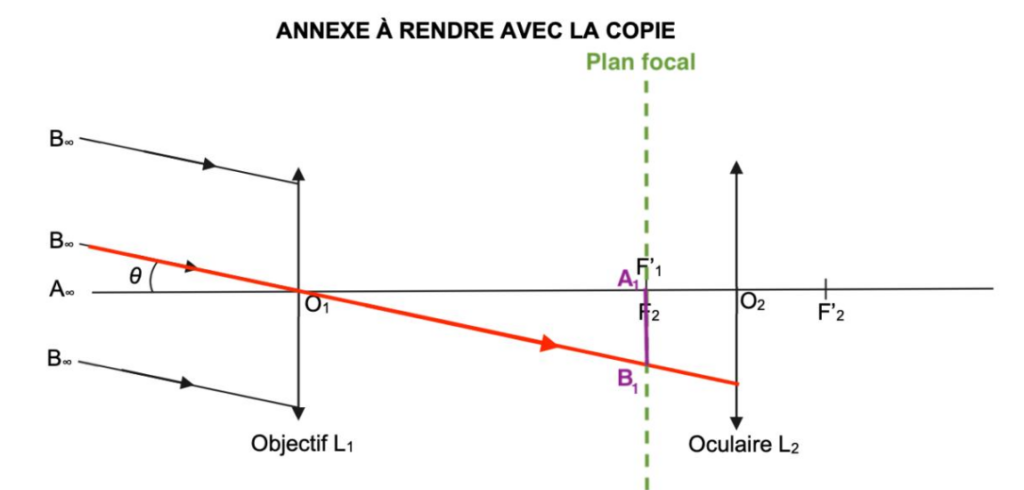
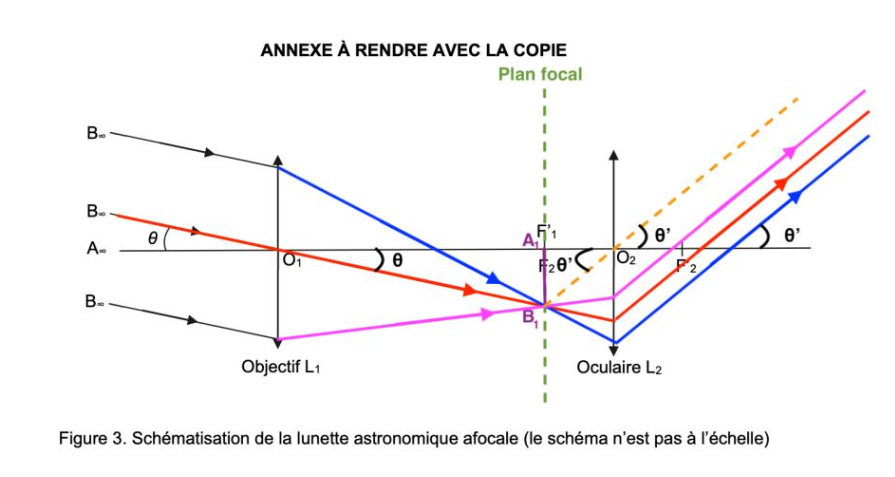
On modélise la lunette astronomique étudiée par un système de deux lentilles minces convergentes notées L₁ et L₂ comme représenté sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE. Cette lunette est constituée d’un objectif (lentille L₁) et d’un oculaire (lentille L₂), dont les centres optiques sont notés respectivement O₁ et O₂ et dont les foyers images sont représentés par F’₁ et F’₂. Le foyer image F’₁ de l’objectif est par ailleurs confondu avec le foyer objet F₂ de l’oculaire.

Sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE, la planète Neptune est modélisée par un objet AB situé à l’infini. Le point A est situé sur l’axe optique. Les rayons qui arrivent de A sont parallèles à l’axe optique. Le point B est situé en dehors de l’axe optique. Les rayons issus de B sont parallèles entre eux et atteignent la lentille L₁ avec une inclinaison θ par rapport à l’axe optique.

Q7. Expliquer pourquoi la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE représente une lunette astronomique afocale.

Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
Neptune est considéré à l’infini : la lentille L₁ donne de Neptune une image sur le foyer image F’₁.
Or les deux foyers F’₁ et F₂ sont confondus.
La lentille L₂, donne de l’objet A₁B₁ situé sur le foyer F₂, une image à l’infini
Ainsi, la lunette astronomique donne d’un objet à l’infini une image à l’infini : elle est afocale.

Q8. Sur la figure 3 de l’ANNEXE À RENDRE AVEC LA COPIE, compléter la marche des trois rayons lumineux du faisceau incident issu de B déjà tracés et traversant l’ensemble de la lunette.

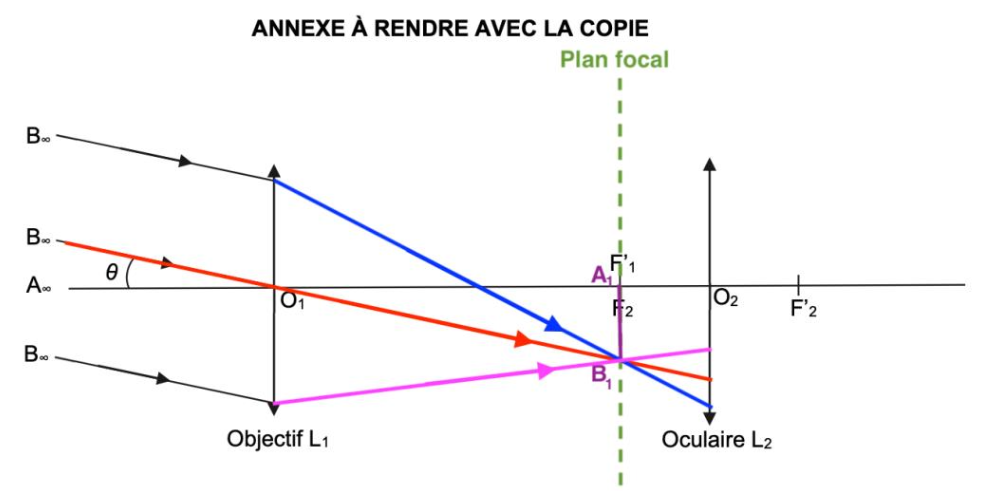
Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O₁ de la lentille L₁ n’est pas dévié.

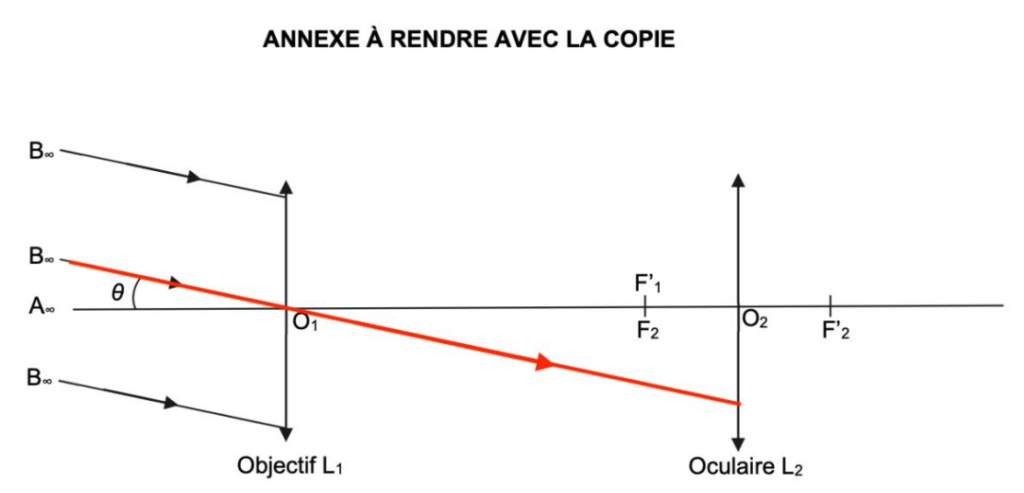
Position de B₁ image intermédiaire de B : Comme l’objet A_∞B_∞ est à l’infini, son image A₁B₁ est dans le plan focal image de l’objectif L₁.

Les autres rayons lumineux issus de B, sortent de L₁ en passant par B₁.

Pour le rayon émergeant de la lentille L₂ :

On trace un rayon issu de B₁ passant par O₂. Ce rayon ne sera pas dévié.

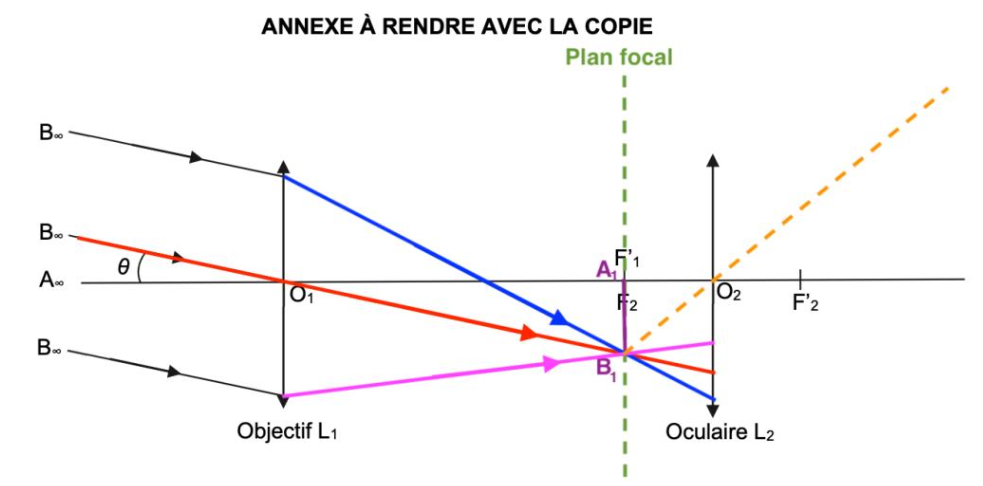
De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi les rayons émergeants de la lentille L₂ issue de B₁ seront parallèles à ce rayon tracé.

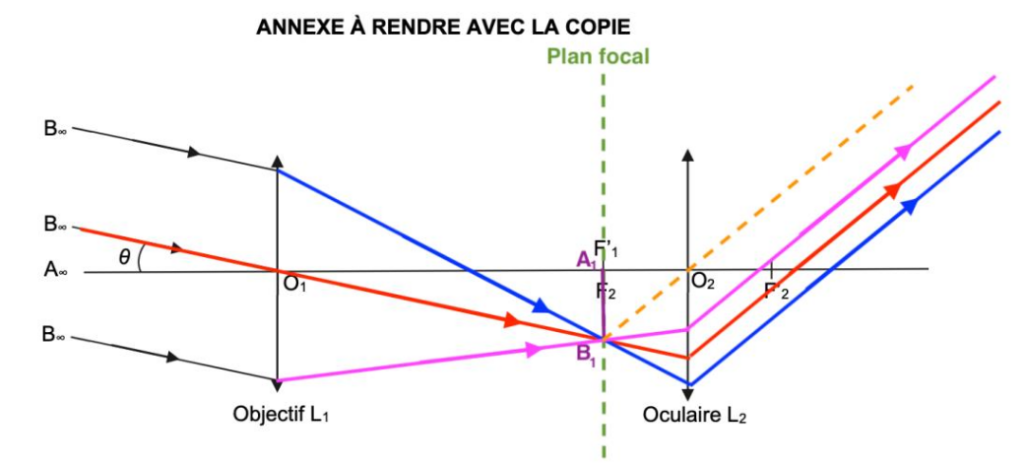
On note θ’ l’angle sous lequel on voit l’image donnée par la lunette astronomique et $G=\frac{\theta’}{\theta}$ le grossissement de celle-ci.

On donne deux caractéristiques de la lunette astronomique présente à l’Observatoire de Berlin en août 1846 :

distance focale de l’objectif : f ’₁ = 4,27 m ;
distance focale de l’oculaire : f ’₂ = 28 mm.

On négligera les effets liés à la diffraction lors de l’observation de Neptune avec cette lunette astronomique.

Le Verrier a écrit : « non seulement on pourra apercevoir la nouvelle planète dans les bonnes lunettes, mais encore on la distinguera par l’amplitude de son disque ; son apparence ne sera pas réduite à celle d’une étoile [ponctuelle]. ».

Q9. Après avoir établi l’expression du grossissement G en fonction des distances focales f ’₁ et f ’₂, calculer la valeur de l’angle θ’ sous lequel Galle a pu observer Neptune avec la lunette astronomique de l’observatoire de Berlin. Commenter la phrase de Le Verrier.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et doit être correctement présentée.

Le grossissement G d’une lunette astronomique est défini par :
$G=\frac{\theta^\prime}{\theta}$

$\tan\left(\theta\right)\approx \theta=\frac{A_1B_1}{f_1^\prime}$
$\tan\left(\theta^\prime\right)\approx \theta^\prime=\frac{A_1B_1}{f_2^\prime}$

$G=\frac{\theta^\prime}{\theta}=\frac{\frac{A_1B_1}{f_2^\prime}}{\frac{A_1B_1}{f_1^\prime}}=\frac{A_1B_1}{f_2^\prime}\times\frac{f_1^\prime}{A_1B_1}=\frac{f_1^\prime}{f_2^\prime}$

Ainsi
$\frac{\theta^\prime}{\theta}=\frac{f_1^\prime}{f_2^\prime}$
$\theta^\prime=\frac{f_1^\prime}{f_2^\prime}\times \theta$
$\theta^\prime=\frac{4,27}{28\times {10}^{-3}}\times 1,1\times {10}^{-5}$
$\theta^\prime=1,7\times {10}^{-3}\ rad$
D’après les données : « pouvoir séparateur de l’œil : on peut distinguer deux points différents d’un astre si l’angle sous lequel on voit ces deux points depuis la Terre est supérieur ou égal à 3×10–4 rad environ »
Avec la lunette $\theta^\prime=1,7\times {10}^{-3}\ rad>3\times {10}^{-4}\ rad$ : Neptune est visible avec la lunette et on distingue les deux points correspondant à son diamètre.
Cela correspond à la phrase de Le Verrier a écrit : « non seulement on pourra apercevoir la nouvelle planète dans les bonnes lunettes, mais encore on la distinguera par l’amplitude de son disque ; son apparence ne sera pas réduite à celle d’une étoile [ponctuelle]. ».

ANNEXE À RENDRE AVEC LA COPIE

Figure 3. Schématisation de la lunette astronomique afocale (le schéma n’est pas à l’échelle)