Centres étrangers 2025 Sujet 1
Exercice 3 – (5 points) – Durée 0h53 – Calculatrice autorisée
Sujet n°25-PYCJ1G11
Sujet et corrigé
EXERCICE 3 : LA FACE CACHÉE DE LA LUNE (5 POINTS)
La Lune est le satellite naturel de la Terre qui a été étudié, voire exploré, sous différents angles et qui continue de fasciner.

Données :
- Constante de gravitation universelle : G = 6,67×10-11 m3·kg-1·s-2 ;
- Masse de la Lune : ML = 7,34×1022 kg ;
- Masse de la Terre : MT = 5,97×1024 kg ;
- Rayon de la Lune : RL = 1,74×106 m ;
- Distance moyenne du centre de la Terre à la Lune : dT-L = 384 400 km ;
- Distance moyenne du centre de la Terre au satellite relais Queqiao 2 : dT-Q = 449 600 km ;
- Distance moyenne satellite relais Queqiao 2 – Chang’e 6 : dQ-C = 65 000 km ;
- La célérité de la lumière dans le vide est supposée connue.
1. La Lune sous tous les angles
Dans cette partie, la Lune est modélisée par un point matériel $L$, de masse $M_L$, en orbite supposée circulaire à la distance $d_{T-L}$ du centre de la Terre $T$, de masse $M_T$. Le mouvement de la Lune est étudié dans le référentiel géocentrique supposé galiléen. La seule interaction gravitationnelle prise en compte est celle entre la Terre et la Lune.
Q.1. Schématiser, sans souci d’échelle, la Terre et la Lune. Placer le repère de Frenet centré sur la Lune $(\vec{u}_N,\vec{u}_T)$ et représenter la force à laquelle est soumise la Lune.
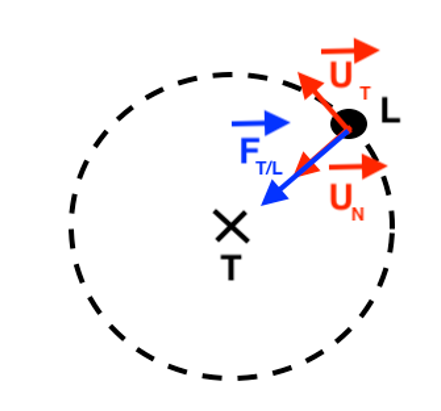
Q.2. Donner dans le repère de Frenet, l’expression vectorielle de la force à laquelle est soumise la Lune.
$$\overarrow{F_{T/L}}=G\times\frac{M_T\times M_L}{d_{TL}^2}\overarrow{u}_N$$
Q.3. Déduire de la seconde loi de Newton appliquée à la Lune, l’expression de la période de révolution de la Lune autour de la Terre :
$$T = 2\pi\sqrt{\dfrac{d_{T-L}^3}{G\times M_T}}$$
Système : Lune
Référentiel : Géocentrique supposé galiléen.
D’après la 2nd loi de Newton :
$\Sigma \overrightarrow {F_{ext}}=M_L\overrightarrow {a}$
$\overrightarrow {F_{T/L}}=M_L\overrightarrow {a}$
$$G\times\frac{M_T\times M_L}{d_{TL}^2} \overrightarrow{ u}_N=M_L \overrightarrow {a}$$
$$\overrightarrow{a}=G\times\frac{M_T}{d_{TL}^2} \overrightarrow {u}_N$$
Pour un mouvement circulaire, dans le repère de Frenet, le vecteur accélération est de la forme :
$$\overrightarrow{a}=\frac{v^2}{d_{TL}}\overrightarrow {u}_N+\frac{dv}{dt}\overrightarrow{u}_T$$
L’accélération étant unique, par identification :
$$\frac{v^2}{d_{TL}}=G\times\frac{M_T}{d_{TL}^2}$$
$$v^2=G\times\frac{M_T}{d_{TL}}$$
$$v=\sqrt{G\times\frac{M_T}{d_{TL}}}$$
$$v=\sqrt{\frac{G\times M_T}{d_{TL}}}$$
La période de révolution est :
$T=\dfrac{\text{Périmètre d’un cercle}}{\text{vitesse}}=\dfrac{2\pi\times d_{TL}}{v}
=2\pi\times\sqrt{d_{TL}\times\dfrac{d_{TL}}{G\times M_T}}
=2\pi\times d_{TL}\times\sqrt{\dfrac{d_{TL}}{G\times M_T}}$
$$T=2\pi\sqrt{\frac{d_{TL}^3}{G\times M_T}}$$
Q.4. Calculer la valeur de la période de révolution $T$ de la Lune autour de la Terre. Sachant que la Lune tourne sur elle-même en environ 28 jours, expliquer pourquoi on ne voit qu’une seule face de la Lune.
$$T=2\pi\sqrt{\frac{d_{TL}^3}{G\times M_T}}$$
$$T=2\pi\sqrt{\frac{\left(384\ 400\times 10^3\right)^3}{6,67\times 10^{-11}\times 5,97\times 10^{24}}}$$
$$T=2,37\times 10^6\ \mathrm{s}$$
$$T=\frac{2,37\times 10^6}{24\times 60\times 60}$$
$$T=27,4\ J$$
Ce temps trouvé est similaire au temps que la Lune tourne sur elle-même en environ 28 jours.
Ainsi, comme le temps que met la Lune à tourner sur elle-même est identique au temps qu’elle met à tourner autour de la Terre, on ne voit qu’une seule face de la Lune.
2. Comment bien communiquer ?
Après plusieurs explorations sur la face visible de la Lune, la Chine a mis en place une mission pour explorer la face cachée de la Lune. La mission utilise une sonde appelée Chang’e 6, du nom de la déesse de la Lune dans la mythologie chinoise.
Les services de communication ont besoin d’un satellite relais pour pouvoir interagir avec la sonde Chang’e 6 qui, du fait de sa position sur la face cachée ne peut pas interagir directement avec les instruments de communication sur Terre. Le 20 mars 2024, la Chine a donc envoyé en orbite lunaire le satellite relais Queqiao 2. Celui-ci a été placé sur une orbite optimisée (figure 2) pour assurer le relais depuis la face cachée.

Figure 2. Schéma de principe de la mission Chang’e 6 (Source : trustmyscience.com)

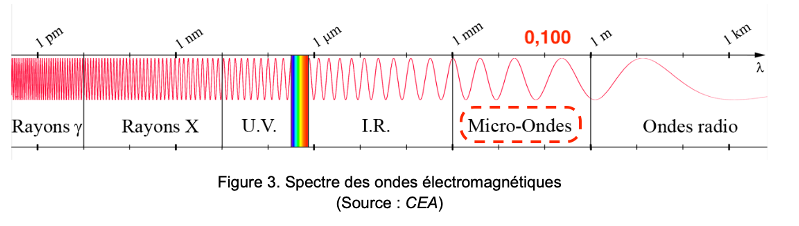
Figure 3. Spectre des ondes électromagnétiques (Source : CEA)
La bande UHF est une bande de communication par signaux électromagnétiques de fréquences comprises entre 300 MHz et 3000 MHz.
Q.5. Déterminer les longueurs d’onde associées à ces signaux électromagnétiques. En déduire le domaine spectral auxquelles ils appartiennent.
$$c=\lambda\times f$$
$$\lambda\times f=c$$
$$\lambda=\frac{c}{f}$$
Pour $f=300\ \rm MHz$
$$\lambda=\frac{c}{f}$$
$$\lambda=\frac{3,00{\times10}^8}{300{\times10}^6}$$
$$\lambda=1,00\ m$$
Pour $f=3000\ \rm MHz$
$$\lambda=\frac{c}{f}$$
$$\lambda=\frac{3,00{\times10}^8}{3000{\times10}^6}$$
$$\lambda=0,100\ m$$
Ces signaux électromagnétiques appartiennent au domaine spectral des Micro-Ondes.
Q.6. Estimer la durée nécessaire pour que l’information émise depuis la station terrienne parvienne à Chang’e 6. Commenter.
$$c=d\Delta t$$
$$c\times\Delta t=d$$
$$\Delta t=\frac{d}{c}$$
Ainsi
$$d=d_{T-Q}+d_{Q-C}$$
D’où
$$\Delta t=\frac{d_{T-Q}+d_{Q-C}}{c}$$
$$\Delta t=\frac{449600\times10^3+65000\times10^3}{3,00\times10^8}$$
$$\Delta t=1,72\ s$$
La communication n’est pas en direct, il y’a un léger décalage de 1,72 s.
3. L’exploration lunaire
Chang’e 6 contient des appareillages permettant l’étude de différents paramètres de la face cachée de la Lune dont un instrument français nommé DORN développé à Toulouse.
DORN (Detection of Outgassing Radon) est un spectromètre alpha (ou à noyau d’hélium) constitué de détecteurs qui mesurent l’activité du radon en comptant les noyaux d’hélium créés lors de la désintégration du radon.

Les mesures effectuées lors de la mission Chang’e 6 montrent une activité du radon constante.
Le radon $^{222}_{86}\text{Rn}$ est un gaz rare inerte issu de la désintégration radioactive de l’uranium $^{238}_{92}\text{U}$ via le radium $^{226}_{88}\text{Ra}$ dans le sous-sol lunaire.
Données :
– Demi-vies :
• 4,5 milliards d’années pour $^{238}\text{U}$ ;
• 1 600 ans pour $^{226}\text{Ra}$ ;
• 4 jours pour $^{222}\text{Rn}$.
Q.7. Écrire l’équation de désintégration nucléaire pour passer du radium 226 au radon 222. En déduire le type de radioactivité.
Équation de désintégration nucléaire pour passer du radium 226 au radon 222 :
$${{88}^{226}}Ra\rightarrow {{86}^{222}}Rn+{_{Z}^{A}}X$$
Conservation du nombre de nucléons :
$$226=222+A$$
$$A=4$$
Conservation du nombre de charge :
$$88=86+Z$$
$$Z=2$$
Ainsi
$${{Z}^{A}}X={{2}^{4}}He$$
Équation complète :
$${{88}^{226}}Ra\rightarrow{{86}^{222}}Rn+{_{2}^{4}}He$$
Le radon 222 est le traceur idéal du dégazage lunaire car il est libéré du sous-sol lunaire et diffusé jusqu’à sa surface où il se désintègre.
Q.8. Définir la demi-vie d’un noyau radioactif.
La demi-vie est la durée nécessaire pour que la moitié des noyaux initialement présents se soient désintégrés.
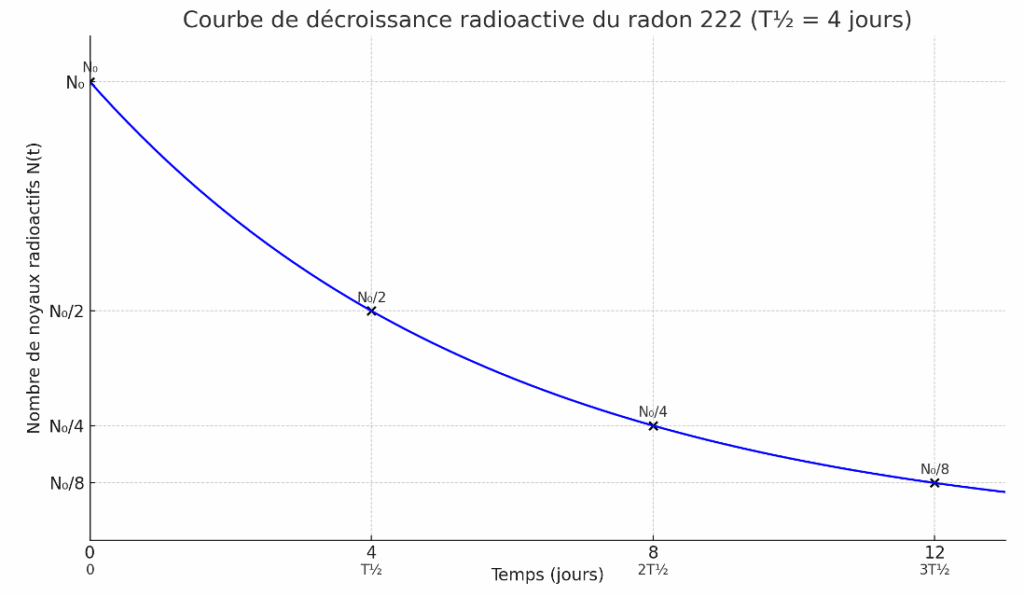
Q.9. Tracer l’allure de la courbe d’évolution de décroissance radioactive du radon 222, $N = f(t)$, d’un échantillon ayant une population initiale $N_0$ de noyaux radioactifs. Représenter la demi-vie du radon 222 sur cette courbe.
Caractéristiques à tracer
- À t = 0, N=N0,
- À t=t1/2 , N=N0/2
- À t=2t1/2 , N=N0/4
- À t=3t1/2 , N=N0/8
- La courbe tend vers 0 mais ne l’atteint jamais.
Q.10. Justifier à l’aide des données fournies pour les différents noyaux radioactifs pourquoi le radon 222 est un traceur adapté à l’étude du dégazage lunaire sur une durée d’une semaine.
Le radon 222 possède une demi-vie de 4 jours, ce qui lui permet de subsister sur une durée comparable à une semaine. Contrairement à des noyaux ayant une demi-vie trop longue, il permet de détecter un dégazage récent.
Il est donc adapté pour tracer des événements lunaires de quelques jours.
