Bac Polynésie 2021 Sujet 2
Exercice C – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée
Sujet n° 21-PYCJ1PO1
Sujet et corrigé
Mots-clés : Lunette astronomique, lentilles convergentes, grossissement.

Figure 1.
La « Grande
Lunette » de Meudon
Jules Janssen (Paris 1824, Meudon 1907) était un astronome français. Il a été à l’origine de la restauration du château de Meudon pour y fonder un observatoire entièrement dédié à l’astrophysique. Dès 1876, il commença à y installer divers instruments d’observation. La « Grande Lunette » (figure 1) y a été mise en service en 1896 sous une coupole de vingt mètres de diamètre. Elle est encore aujourd’hui la plus grande lunette astronomique d’Europe.
Le but de cet exercice est de modéliser la « Grande Lunette » puis de calculer l’angle sous lequel on observe l’image d’un cratère de la Lune à travers cette lunette.
Données :
La « Grande Lunette » est constituée de deux lentilles minces convergentes :
- une lentille L1 de centre optique O1 de distance focale f1‘ = 16 m,
- une lentille L2 de centre optique O2 de distance focale f2‘= 4 cm.
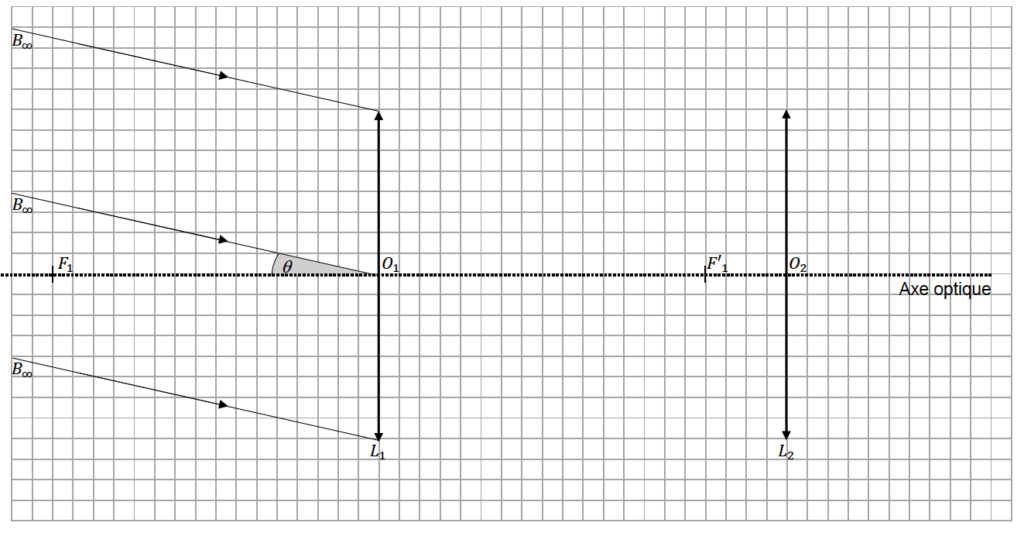
Sur le document réponse à rendre avec la copie, le modèle de la « Grande Lunette » est représenté sans souci d’échelle.
1. En utilisant ce document à rendre avec la copie, nommer la lentille L1 et la lentille L2. Justifier les noms attribués.
L1 : l’objectif car c’est une lentille convergente possédant une grande distance focale. C’est la lentille placée vers l’objet
L2 : l’oculaire car c’est une lentille convergente possédant une petite distance focale. C’est la lentille où on place l’œil.
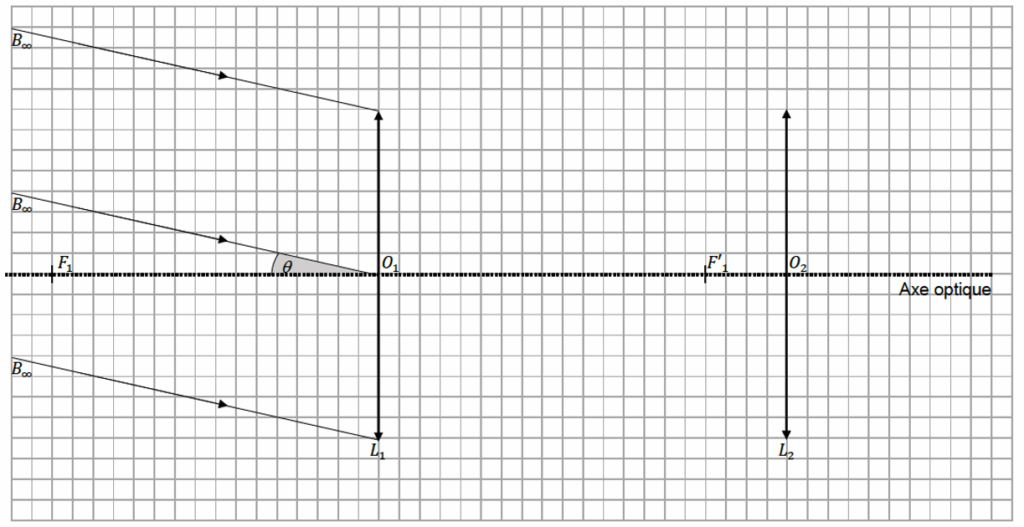
2. Une lunette astronomique est un système optique « afocal ». Donner la définition du terme « afocal ».
Un système optique est dit afocal s’il donne d’un objet à l’infini une image à l’infini.
Lorsque les deux foyers $F_1’$ et $F_2$ sont confondus alors la lunette est afocale.
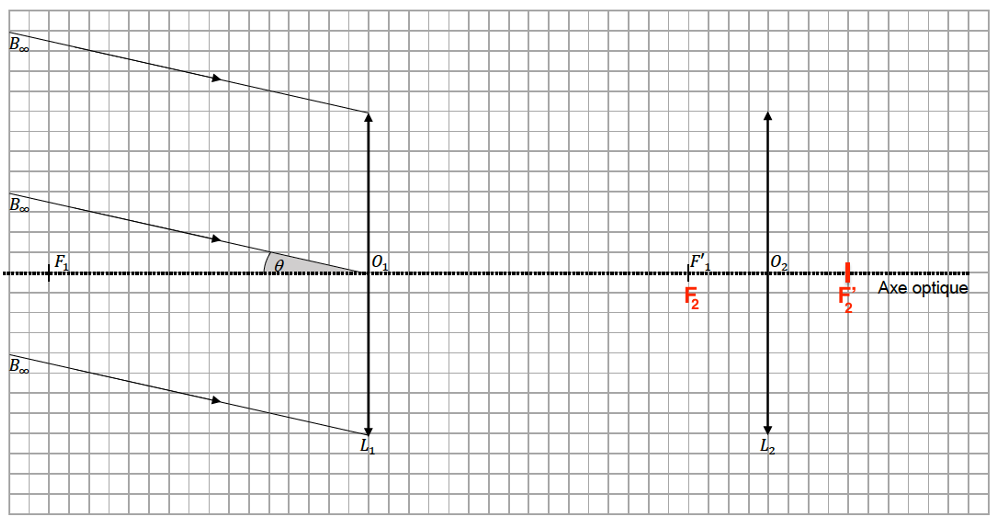
3. Sur le document réponse à rendre avec la copie, indiquer la position des foyers objet F2 et image F’2 de la lentille L2 sans souci d’échelle.
Comme la lunette est afocale, on place $F_2$ sur $F_1’$.
La distance $OF_2′ = OF_2$.
La lunette astronomique représentée sur le document réponse à rendre avec la copie est utilisée pour observer un point objet B situé « à l’infini » qui émet un faisceau lumineux parallèle vers la lunette. Le faisceau pénètre dans la lunette en s’appuyant sur les bords de la lentille L1. La lentille L1 donne de ce point B une image appelée image intermédiaire notée B1.
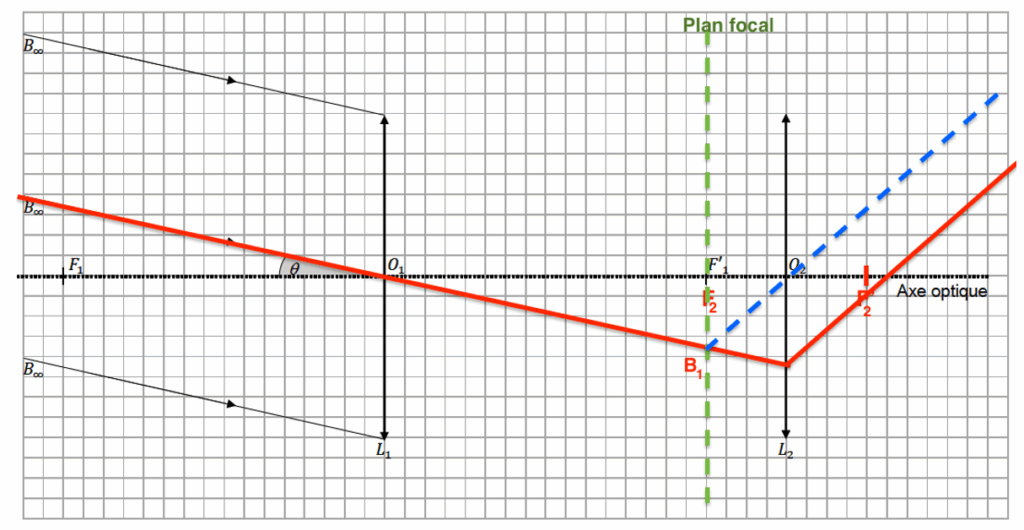
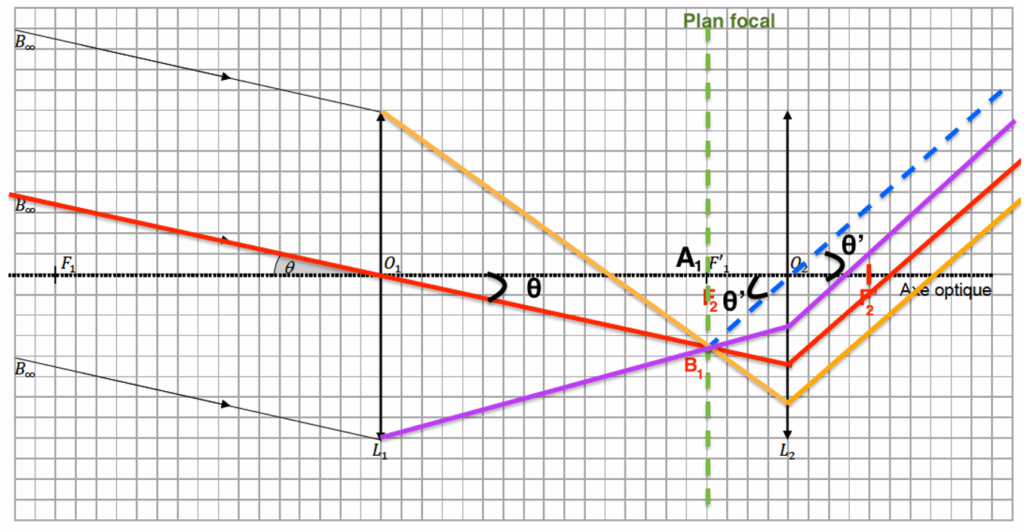
4. Sur le document réponse à rendre avec la copie, tracer le trajet du rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 et émergeant de la lentille L2. Noter la position de B1 image intermédiaire de B.
Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O1 de la lentille L1 n’est pas dévié.
Position de B1 image intermédiaire de B : Comme l’objet A∞B∞ est à l’infini, son image A1B1 est dans le plan focal image de l’objectif L1.
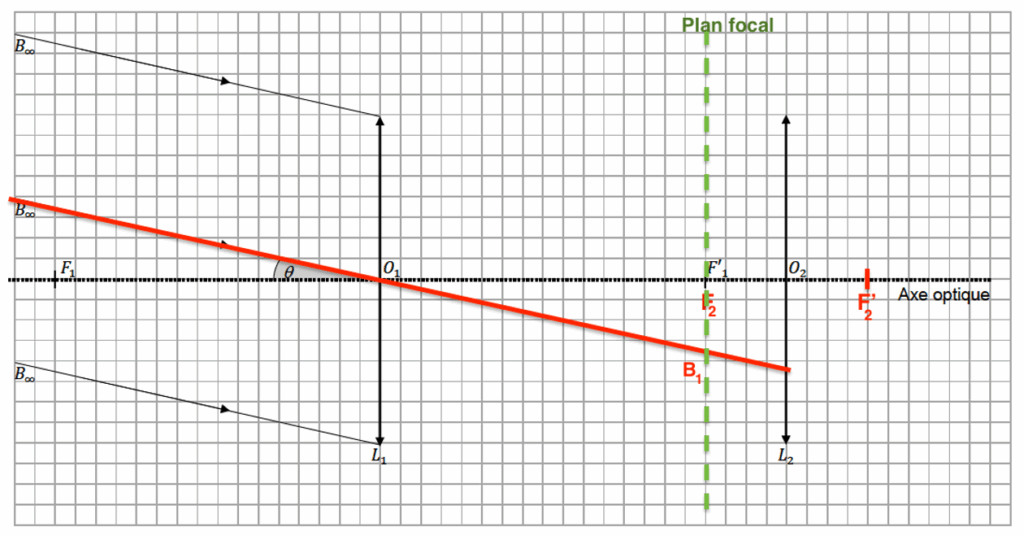
Pour le rayon émergeant de la lentille L2 :
On trace un rayon issu de B1 passant par O2. Ce rayon ne sera pas dévié. De plus nous savons que l’image d’un objet situé dans le plan focal objet d’une lentille se forme à l’infini. Ainsi le rayon émergeant de la lentille L2 issue de B1 sera parallèle à ce rayon tracé
5. Représenter le faisceau émergent issu de l’objet B traversant la lunette en poursuivant les trajets des rayons lumineux s’appuyant sur les bords de la lentille L1 jusqu’à leur sortie de la lunette par L2 sur le document réponse à rendre avec la copie.
Les rayons lumineux s’appuyant sur les bords de la lentille L1 sont issus de B. Ainsi, ils seront déviés vers B1.
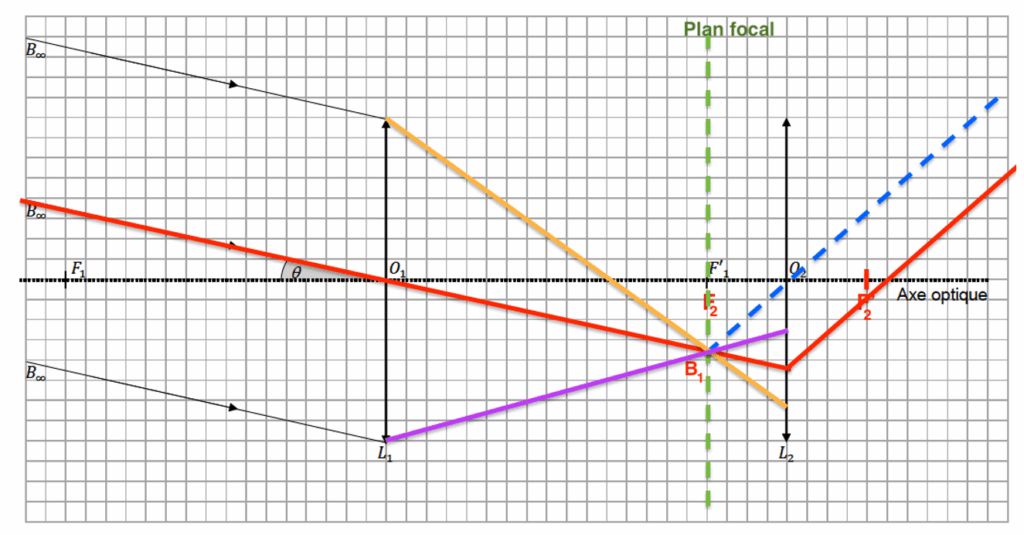
Pour leur sortie de la lunette par L2, les rayons seront parallèles aux autres rayons déjà tracés issus de B1 passant par la lentille L2.
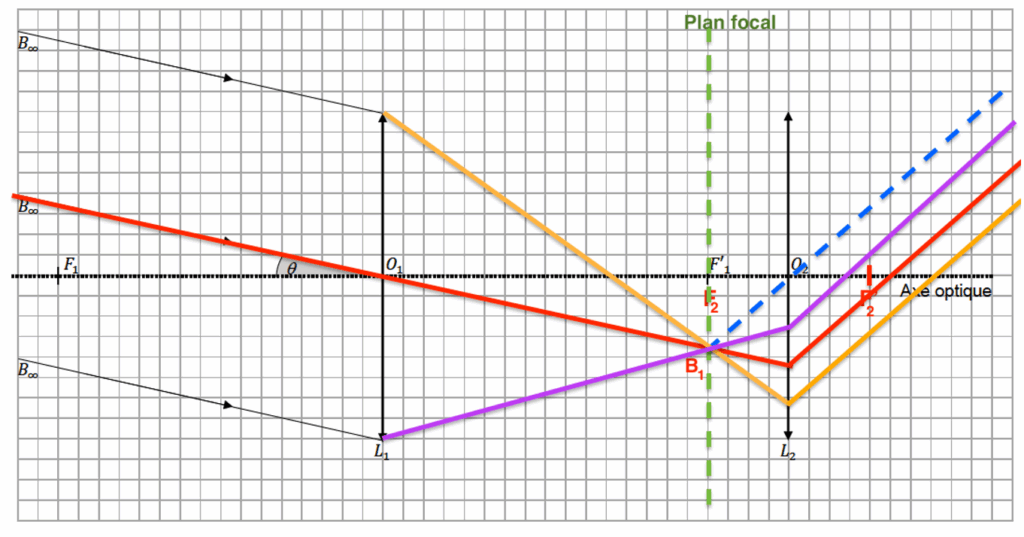
6. Le point objet B est vu à l’œil nu sous l’angle θ appelé diamètre apparent de l’objet. Représenter l’angle θ’ sous lequel l’image définitive est vue à travers la lunette sur le document réponse à rendre avec la copie.
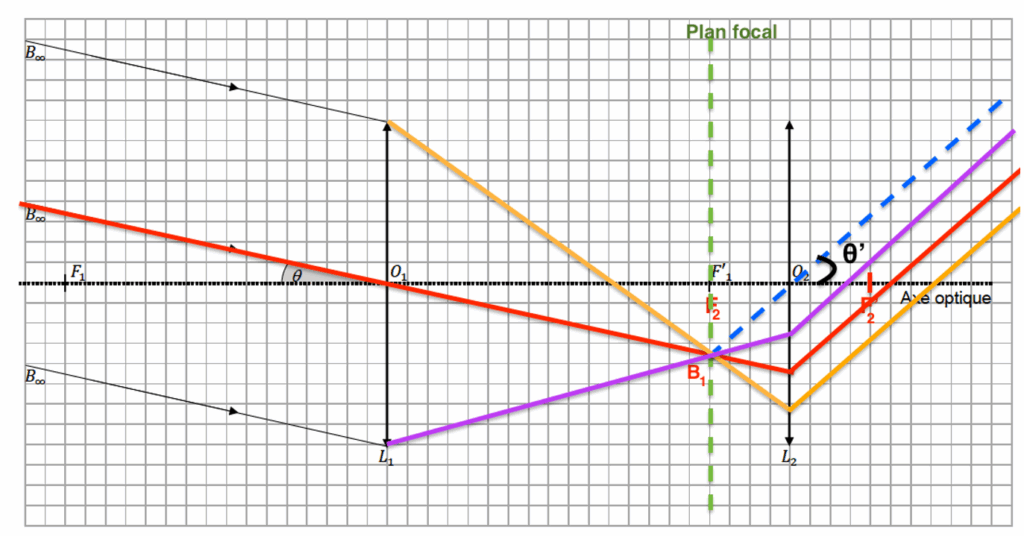
7. Le grossissement de la lunette est donné par l’expression :
$G= \frac{\theta’}{\theta} $
Les angles θ ’ et θ sont petits et exprimés en radian, on peut donc considérer que tan θ = θ et que tan θ ′= θ ′. Retrouver, par des considérations géométriques, l’expression du grossissement G en fonction des distances focales f1‘ et f2‘ .
$$\tan(\theta) \approx \theta = \frac{A_1B_1}{f_1′}$$
$$\tan(\theta’) \approx \theta’ = \frac{A_1B_1}{f_2′}$$
$$G = \frac{\theta’}{\theta} = \frac{\frac{A_1B_1}{f_2′}}{\frac{A_1B_1}{f_1′}} = \frac{A_1B_1}{f_2′} \times \frac{f_1′}{A_1B_1} = \frac{f_1′}{f_2′}$$
8. Calculer le grossissement GGL de la « Grande Lunette » de Meudon.
$$G_{GL} = \frac{f_1′}{f_2′}$$
$$G_{GL} = \frac{16}{4\times10^{-2}} = 4\times10^2$$
Depuis le sol terrestre, un cratère de la Lune nommé Albategnius peut être aperçu sous un angle θ de valeur égale à 1’.
Donnée : Un degré est subdivisé en 60 minutes d’arc dont la notation est 60 ’.
9. Calculer, en degrés, la valeur de l’angle θ’ sous lequel l’image du cratère Albategnius est observé à travers la « Grande Lunette » de Meudon.
| 1° | 60’ |
| $\theta$ | 1’ |
$$\theta = \frac{1 \times 1}{60} = 1,7\times10^{-2}\ \text{degrés}$$
$$G = \frac{\theta’}{\theta}$$
$$\theta’ = G\times\theta$$
$$\theta’ = 4\times10^2 \times 1,7\times10^{-2}$$
$$\theta’ = 6,8\ \text{degrés}$$
EXERCICE C – La « Grande Lunette » de Meudon DOCUMENT RÉPONSE À RENDRE AVEC LA COPIE
Questions 3, 4, 5 et 6