La masse de la Terre

Bac Polynésie 2024 Sujet 2

Exercice 2 – (6 points) –  Durée 1h03 – Calculatrice autorisée

Sujet n°24-PYCJ2PO1

EXERCICE 2 – LA MASSE DE LA TERRE (6 POINTS)

De tout temps, l’Homme a cherché à mesurer ce qui l’entoure de l’infiniment petit à l’infiniment grand. Il a donc dû mettre en place des protocoles de mesure indirecte pour accéder aux dimensions des objets hors de sa portée.

L’objectif de cet exercice est de mesurer la masse de la Terre par deux méthodes.

Mesure de la masse de la Terre à l’aide d’un satellite.

On étudie le mouvement du centre de masse A d’un satellite, dans le référentiel géocentrique, considéré comme galiléen. Ce satellite est situé à une distance r = OA par rapport au centre O de la Terre.

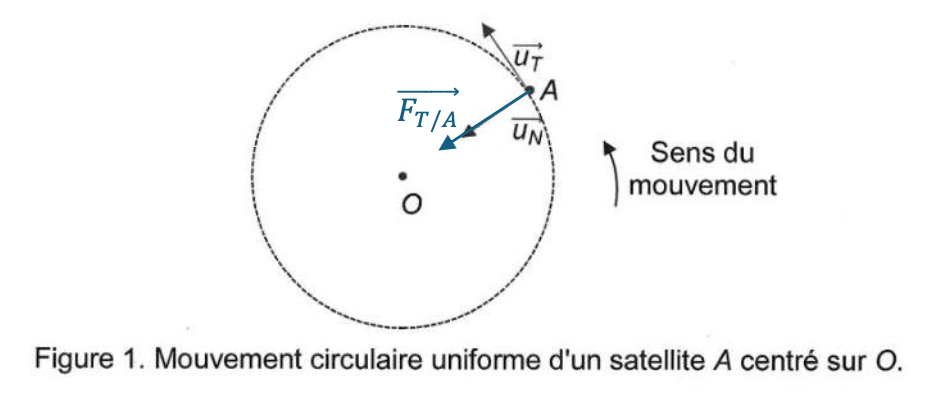
On fait l’approximation, dans un premier temps, que le mouvement du satellite est circulaire uniforme et on considère que la seule force qui s’applique sur le satellite est la force d’interaction gravitationnelle $\overrightarrow{F_{T/A}}$ exercée par la Terre, de masse M_T sur le satellite, de masse m.

Le repère de Frenet $(A,\overrightarrow{u_T},\overrightarrow{u_N})$ est représenté figure 1.

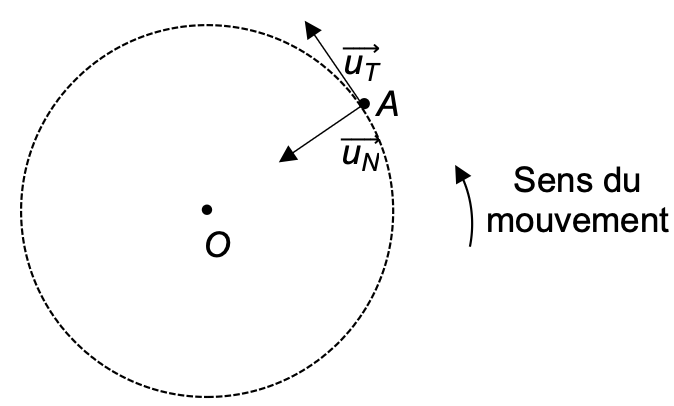
Figure 1. Mouvement circulaire uniforme d’un satellite A centré sur O.

Q1. Reproduire la figure 1 sur votre copie et représenter sans souci d’échelle, la force d’interaction gravitationnelle $\overrightarrow{F_{T/A}}$ exercée par la Terre sur le satellite.

On note G la constante de gravitation universelle.

Q2.Donner l’expression vectorielle de la force gravitationnelle $\overrightarrow{F_{T/A}}$ en fonction du vecteur unitaire $\overrightarrow{u_{N}}$, de G, M_T, m et r.

Ici, la force gravitationnelle s’exprime par : $\overrightarrow{F_{T/A}}=\frac{G\times M_T\times m}{r^2}\overrightarrow{u_N}$

Q3. En appliquant la deuxième loi de Newton au centre de masse A du satellite, établir que sa vitesse a pour expression $v=\sqrt{\frac{G\cdot M_T}{r}}$ .

Le système étudié est le satellite de centre de masse A.
Le référentiel d’étude est géocentrique, et le repère étudié est le repère de Frenet $(A,\overrightarrow{u_T},\overrightarrow{u_N})$.
Le satellite est soumis à la force gravitationnelle $\overrightarrow{F_{T/A}}$.
D’après la deuxième loi de Newton : $\sum\overrightarrow{F_{ext}}=m\cdot\overrightarrow{a}$
On a : $\overrightarrow{F_{T/A}}=m\cdot\overrightarrow{a}$
$\frac{G\times M_T\times m}{r^2}\overrightarrow{u_N}=m\cdot\overrightarrow{a}$
$\frac{G\times M_T}{r^2}\overrightarrow{u_N}=\overrightarrow{a}$
Or, dans le repère de Frenet : $\overrightarrow{a}=\frac{dv}{dt}\overrightarrow{u_T}+\frac{v^2}{r}\overrightarrow{u_N}$
$\frac{G\times M_T}{r^2}\overrightarrow{u_N}=\frac{dv}{dt}\overrightarrow{u_T}+\frac{v^2}{r}\overrightarrow{u_N}$
Par identification : $\frac{dv}{dt}=0$ et $\frac{G\times M_T}{r^2}=\frac{v^2}{r}$
Puisque $\frac{dv}{dt}=0$, donc $a_T=0$. La vitesse du satellite est donc constante, et le satellite a un mouvement circulaire uniforme.
Et on a : $\frac{G\times M_T}{r^2}=\frac{v^2}{r}$
$v^2=\frac{G\times M_T}{r}$
$v=\sqrt{\frac{G\cdot M_T}{r}}$

Q4. À l’aide de l’expression littérale de la vitesse v du satellite et de la définition de la période de révolution T du satellite autour de la Terre, vérifier que l’expression de la troisième loi de Kepler est : $\frac{T^2}{r^3}=\frac{4\pi^2}{G\cdot M_T}$.

Formule : $v=\frac{d}{T}$ avec $d=2\pi r$ et $v=\sqrt{\frac{G\cdot M_T}{r}}$
$\sqrt{\frac{G\cdot M_T}{r}}=\frac{2\pi r}{T}$
$\frac{G\cdot M_T}{r}=\left(\frac{2\pi r}{T}\right)^2$
$\frac{G\cdot M_T}{r}=4\pi^2\frac{r^2}{T^2}$
$\frac{T^2}{r^3}=\frac{4\pi^2}{G\cdot M_T}$

Astérix, le premier satellite artificiel français, a été lancé le 26 novembre 1965, la France devient alors la troisième puissance spatiale mondiale.

On considère que le satellite Astérix A parcourt une trajectoire elliptique autour de la Terre de centre O. Les points B et C symbolisent respectivement le périgée et l’apogée de l’ellipse.

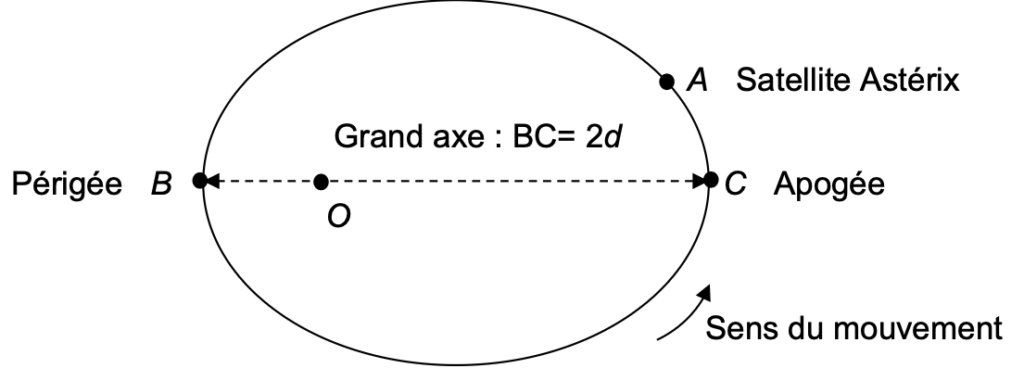
Figure 2. Trajectoire elliptique du satellite Astérix.

Données :

• Grand axe : BC = 2d ;
• Distance entre le périgée et le centre de la Terre : D_OB = 6,89×10⁶ m ;
• Distance entre l’apogée et le centre de la Terre : D_OC = 8,07×10⁶ m ;
• Constante de gravitationnelle universelle : G = 6,67×10^–11 m³·kg^–1·s^–2.

Q5. En vous aidant de la figure 2 et des données, calculer la valeur du demi-grand axe d de l’ellipse de la trajectoire du satellite Astérix.

On a $BC=D_{OB}+D_{OC}=2d$. Donc $d=\frac{D_{OB}+D_{OC}}{2}$.
A.N. : $d=\frac{(6,89+8,07)\times{10}^6}{2}=\frac{14,96\times{10}^6}{2}=7,48\times{10}^6\ m$

Dans le cas d’une trajectoire elliptique, la troisième loi de Kepler établie à la question Q4 s’écrit en remplaçant la valeur du rayon de la trajectoire circulaire par la valeur du demi-grand axe de la trajectoire elliptique. Ainsi, on obtient l’expression : $\frac{T^2}{d^3}=\frac{4\pi^2}{G\cdot M_T}$ .

Donnée :

• Le satellite Astérix effectue 1400 révolutions autour de la Terre en une durée Δt d’une valeur égale à 9,03×10⁶ s.

Q6. En exploitant l’expression de la période T de révolution d’un satellite en orbite elliptique, calculer la masse M_T de la Terre.

Le satellite Astérix fait 1400 révolutions autour de la Terre en une durée $\Delta t=9,03\times{10}^6\ s$.
Donc le temps pour une révolution est : $T=\frac{9,03\times{10}^6}{1400}=6450\ s=6,45\times{10}^3\ s$.
D’après la troisième loi de Kepler : $\frac{T^2}{d^3}=\frac{4\pi^2}{G\cdot M_T}$
Donc : $M_T=\frac{4\pi^2\times d^3}{G\times T^2}$
A.N. : $M_T=\frac{4\pi^2\times{(7,48\times{10}^6)}^3}{6,67\times{10}^{-11}\times{6450}^2}=5,95\times{10}^{24}\ kg$.
Donc la Terre possède une masse de $5,95\times{10}^{24}\ kg$ environ.

Mesure de la masse de la Terre à l’aide d’un pendule.

On représente les variations de l’angle θ en fonction du temps pour un pendule de longueur ℓ = 1,0 m sur la figure 3.

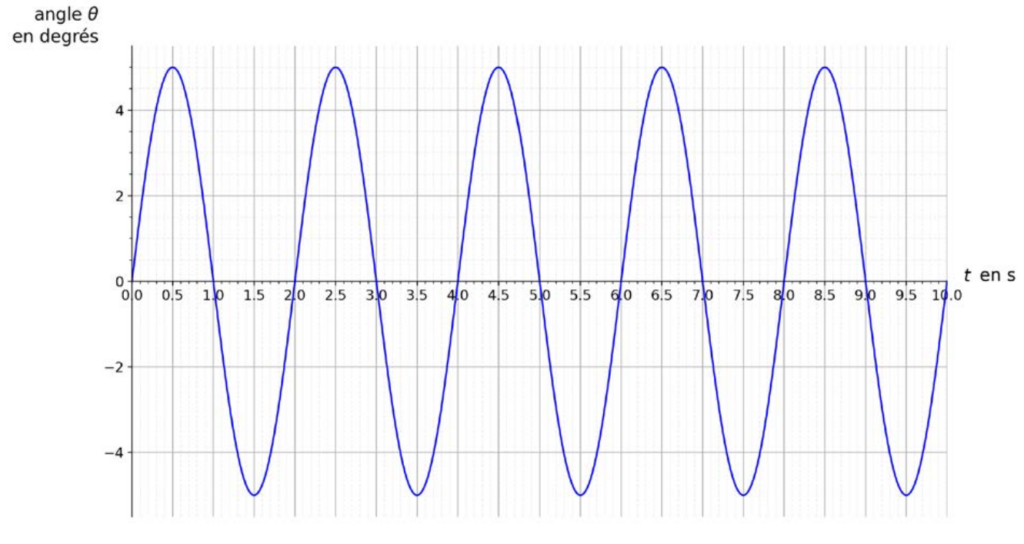
Figure 3. Variations de l’angle θ en fonction du temps.

Q7. Exploiter la figure 3 pour déterminer, le plus précisément possible, la valeur de la période T des oscillations du pendule.

D’après la figure 3, on a 5 oscillations pour une durée $\Delta t=10,0\ s$.
Donc pour une oscillation : $T=\frac{10,0}{5}=2,0\ s$.

On admet que l’expression de la période des oscillations du pendule est $T=2\pi\sqrt{\frac{\ell}{g}}$ avec ℓ la longueur du pendule, en mètres, et T la période des oscillations, en secondes.

Q8. Calculer la valeur de l’intensité de pesanteur g.

On nous donne : $T=2\pi\sqrt{\frac{l}{g}}$
$T^2=4\pi^2\times\frac{l}{g}$
Donc : $g=\frac{4\pi^2\times l}{T^2}$ ;
A.N. : $g=\frac{4\pi^2\times1,0}{4}=\pi^2=9,9\ m.s^{-2}$

Donnée :

• Distance entre le pendule et le centre de la Terre : R_T = 6,37×10³ km.

Q9. En considérant que le poids P du pendule est de valeur égale à la force d’interaction gravitationnelle F exercée par la Terre sur le pendule, déterminer la valeur M_T de la masse de la Terre.

L’expression de la force gravitationnelle exercée par la Terre sur le pendule est : $F=\frac{G\times M_T\times m}{{R_T}^2}$
Le poids s’exprime par : $P=m\times g$
On considère $P=F$
On a : $m\times g=\frac{G\times M_T\times m}{{R_T}^2}$
$g=\frac{G\times M_T}{{R_T}^2}$
Donc : $M_T=\frac{g\times{R_T}^2}{G}$ ;
A.N. : $M_T=\frac{9,9\times{(6,37\times{10}^6)}^2}{6,67\times{10}^{-11}}=6,0\times{10}^{24}\ kg$