La mesure du méridien par triangulation au XVIIIe siècle

Sujet sans enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h – 10 points – Thème « La Terre, un astre singulier »

Dans cet exercice, on cherche à calculer la longueur d’un méridien terrestre en utilisant la méthode de triangulation du XVIIIe siècle.

Document 1 – L’aventure de Delambre et Méchain

Jean-Baptiste Delambre, Pierre Méchain et leurs collaborateurs devaient définir la longueur du mètre, fixée selon les scientifiques de l’Académie des sciences à « la dix millionième partie du quart du méridien terrestre. Ils se lancent pour cela dans la mesure du méridien de Paris : une ligne née dans l’imagination des cartographes, qui traverse la France de part en part (de Dunkerque à Barcelone) et fait le tour de la Terre en passant par les deux pôles. Les deux tiers supérieurs, de Dunkerque à Rodez, incombent à Jean-Baptiste Delambre, et le parcours Rodez- Barcelone à Pierre Méchain. Aucun monument ne commémore les efforts déployés pour mener à bien cette mission, en pleine Terreur (au moment de la Révolution française) …

Les chercheurs utilisent une méthode mathématique appelée « α triangulation ». Elle consiste à diviser le terrain en triangles pour le mesurer. On trace d’abord le long du méridien des triangles jointifs, ayant chacun un côté en commun avec le suivant. Il suffit ensuite de mesurer les angles des triangles par visée, depuis un endroit situé en hauteur (clocher, château, tour) et de disposer de la longueur d’une seule base (celle de Melun-Lieussaint pour la partie nord) pour pouvoir en déduire tous les côtés des triangles dont la somme était précisément la portion de méridien.

Source : D’après Azar Khalatbari, « Le mètre et le méridien », wwwliberation.fr, 2006

Document 2 – La mesure de la distance Dunkerque-Barcelone par Delambre et Méchain

On peut effectuer une triangulation à partir de la connaissance de la longueur d’une première base de 6075,90 toises1 entre Melun et Lieussaint, deux villes situées en Seine-et-Marne (77). Ainsi, à partir des extrémités de cette base, Jean- Baptiste Delambre vise Malvoisine. De la mesure des angles, il déduit la distance Lieussaint-Malvoisine et celle-ci constitue la base d’un nouveau triangle dont le sommet sera Montlhéry. Une chaîne de triangles successifs juxtaposés est ainsi formée le long de la méridienne. L’arc de méridien Dunkerque-Barcelone a pour longueur un quarantième de méridien terrestre.

1 : Toise : unité de longueur ancienne, correspondant à six pieds : 1 toise = 1,949 m

Source : D’après « Un voyage… de Dunkerque à Barcelone », www.clea-astro.eu

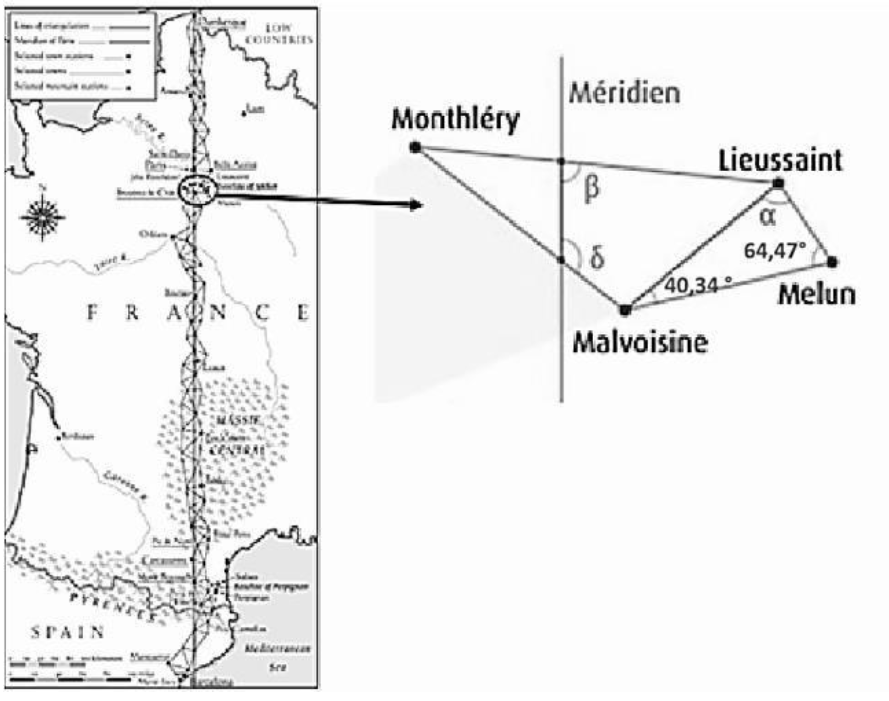
Source : Ken Alder 2005 et IGN

Document 3 – Loi des sinus

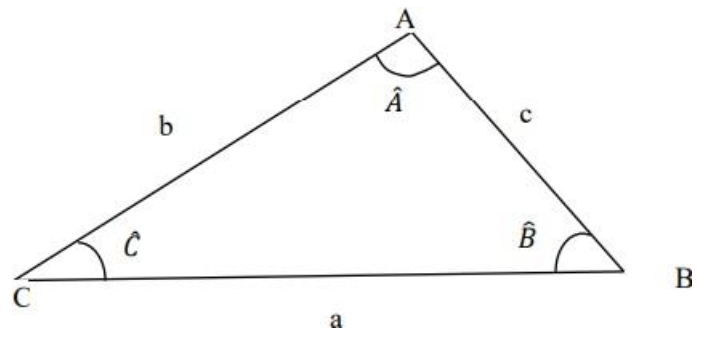
La méthode de triangulation est fondée sur la loi des sinus, formule de trigonométrie dans un triangle quelconque, qui s’énonce de la façon suivante pour un triangle ABC :

$\frac{a}{sin\ \hat{A}}=\frac{b}{sin\ \hat{B}}=\frac{c}{sin\ \hat{C}}$

1 – Montrer que l’angle alpha, qui se réfère à l’angle entre la base Melun-Lieussaint et la ligne de visée vers Malvoisine, du document 2, est égal à 75,19°.

Dans un triangle, la somme des angles vaut 180° :

α +64,47+40,34=180

α =180-64,47-40,34

α =75,19°

Ainsi, l’angle alpha, qui se réfère à l’angle entre la base Melun-Lieussaint et la ligne de visée vers Malvoisine, du document 2, est égal à 75,19°.

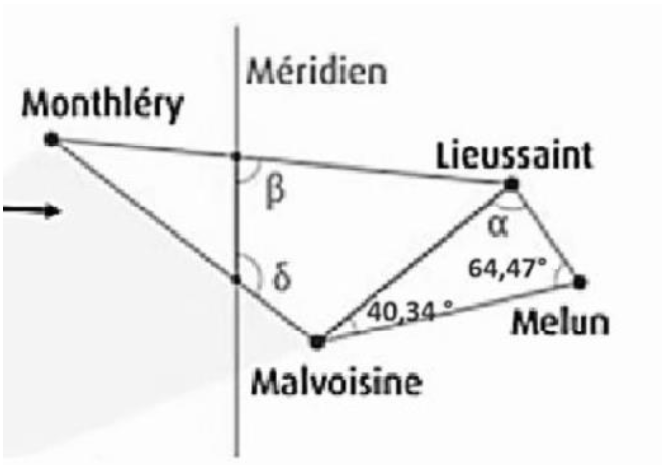
2 – En écrivant la loi des sinus du document appliquée au triangle représenté dans document 3, déterminer la distance Melun-Malvoisine en kilomètre. Arrondir le résultat à 10^-1 près.

D’après la loi des sinus :

$\frac{a}{sin\ \hat{A}}=\frac{b}{sin\ \hat{B}}=\frac{c}{sin\ \hat{C}}$

Appliquons la loi des sinus du document au triangle représenté dans document 3 :

$\frac{d_{Melun-Malvoisine}}{sin\ 75,19}=\frac{d_{Melun-Lieussaint}}{sin\ 40,34}=\frac{d_{Lieussain-Malvoisine}}{sin\ 64,47}$

Le document 2 nous donne : « la longueur d’une première base de 6075,90 toises entre Melun et Lieussaint.

1 : Toise : unité de longueur ancienne, correspondant à six pieds : 1 toise = 1,949 m »

$\frac{d_{Melun-Malvoisine}}{sin\ 75,19}=\frac{d_{Melun-Lieussaint}}{sin\ 40,34}$

$d_{Melun-Malvoisine}=\frac{d_{Melun-Lieussaint}}{sin\ 40,34} \times sin\ 75,19$

$d_{Melun-Malvoisine}=\frac{6075,90}{sin\ 40,34} \times sin\ 75,19$

$d_{Melun-Malvoisine}=9074,4\ toises$

$d_{Melun-Malvoisine}=9074,4 \times 1,949$

$d_{Melun-Malvoisine}=17686,0\ m$

$d_{Melun-Malvoisine}=17,7\ km$

Ainsi, la distance Melun-Malvoisine est de 17,7 kilomètres.

3 – Aujourd’hui on sait que la distance entre ces deux villes est égale à d = 18,2 km. L’incertitude sur la mesure admise est égale à 1,0 km, conclure sur la précision de la mesure de l’époque.

L’incertitude sur la mesure admise est égale à 1,0 km. Ainsi, la valeur trouvée est comprise entre

$17,7\ km-1<d_{Melun-Malvoisine}<17,7\ km+1$

$16,7\ km<d_{Melun-Malvoisine}<18,7\ km$

La distance entre ces deux villes est égale à d = 18,2 km. Cette valeur est dans l’intervalle de valeur de la distance mesurée.

Ainsi, la mesure de l’époque est précise.

4 – En appliquant la méthode de triangulation, Jean-Baptiste Delambre a obtenu une longueur de 1 000 km pour l’arc méridien Dunkerque Barcelone. En déduire à partir document 2 la longueur L du méridien terrestre (circonférence de la Terre).

D’après le document 2 : « L’arc de méridien Dunkerque-Barcelone a pour longueur un quarantième de méridien terrestre. »

Soit

$d_{Dunkerque-Barcelone}=\frac{1}{40} \times L$

$\frac{1}{40} \times L=d_{Dunkerque-Barcelone}$

$L=40 \times d_{Dunkerque-Barcelone}$

$L=40 \times 1000$

$L=40\ 000\ km$

La longueur L du méridien terrestre est de 40 000 km.

5 – Indiquer si le résultat est cohérent avec la définition du mètre du document 1.

D’après le document 1 : « définition de la longueur du mètre, fixée selon les scientifiques de l’Académie des sciences : la dix millionième partie du quart du méridien terrestre »

$40\ 000\ km \times \frac{1}{10 \times {10}^6} \times \frac{1}{4}=40\ 000 \times \ {10}^3 \times \frac{1}{10 \times {10}^6} \times \frac{1}{4}=1,0\ m$