La physique s’invite sur un terrain de rugby

Nouvelle Calédonie 2025 Sujet 2

Exercice 2 – (6 points) – Durée 1h03 – Calculatrice autorisée

Sujet n°25-PYCJ2NC1

EXERCICE II – LA PHYSIQUE S’INVITE SUR UN TERRAIN DE RUGBY (6 points)

Au rugby, une chandelle est un tir au pied vers l’avant et très en hauteur qui permet au tireur, sur sa lancée, de récupérer le ballon à sa retombée avant l’adversaire.

Dans cet exercice, on se propose d’étudier une chandelle par une approche dynamique dans la première partie ; la seconde partie concerne une étude énergétique.

Les parties A et B de cet exercice sont indépendantes et peuvent être traitées séparément.

Lors d’un entrainement, un joueur de rugby réalise une chandelle. Le système considéré est le ballon de rugby, assimilé à un point matériel de centre de masse noté G. Le mouvement du ballon est étudié dans le référentiel terrestre supposé galiléen et muni du système d’axes (Ox, Oz), de base $(O\ ;\ \overrightarrow{i}\ ;\ \overrightarrow{k})$.

À t = 0 s, le joueur communique au ballon, de masse m, une vitesse $\overrightarrow{v_0}$ qui forme un angle α avec l’horizontale. Le ballon se trouve alors à une hauteur h au-dessus du sol comme indiqué sur la figure 1.

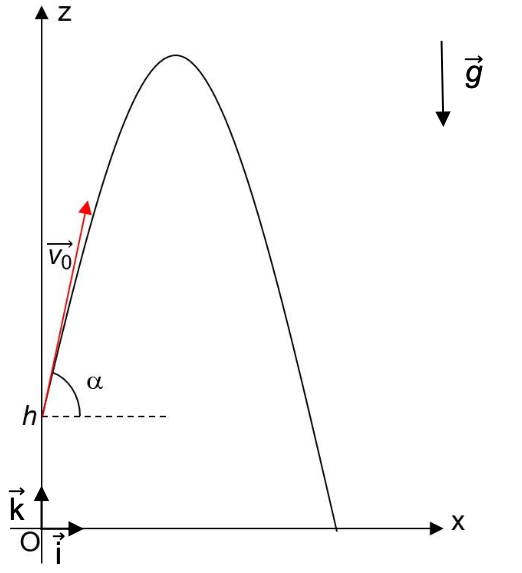
Figure 1 – Schéma de la situation lors de la chandelle

Hypothèses :

La valeur du champ de pesanteur terrestre local $\overrightarrow{g}$ est considérée uniforme.
Les frottements liés à l’action de l’air sont supposés négligeables.

Données :

Intensité de la pesanteur terrestre : g = 9,81 m·s^–2.
Valeur v₀ de la vitesse initiale communiquée au ballon : ~~v₀ = 20,5 km.h^–1~~(erreur du sujet) v₀ = 20,5 m.s^–1
Altitude initiale du ballon : h = 90 cm.
Angle à l’instant initial : α = 70°.

Partie A – Étude dynamique d’une chandelle

1. En précisant la loi utilisée, exprimer les coordonnées du vecteur accélération ballon à l’instant t : a_x(t) et a_z(t).

Système {sphère métallique}
Référentiel terrestre supposé galiléen

D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{P}=m\overrightarrow{a}$$
$$m\overrightarrow{g}=m\overrightarrow{a}$$
$$\overrightarrow{g}=\overrightarrow{a}$$

Or
$$\overrightarrow{g}\begin{pmatrix}0\\-g\end{pmatrix}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.

$$\overrightarrow{a}\begin{pmatrix}a_{x(t)}=0\\a_{z(t)}=-g\end{pmatrix}$$

2. Montrer que les équations horaires du mouvement sont :

$$
\begin{cases}
x(t)=v_0 \times \cos(\alpha) \times t\\
z(t)=-\frac{1}{2} \times g \times t^2+v_0 \times \sin(\alpha) \times t+h
\end{cases}
$$

$$\overrightarrow{a}\begin{pmatrix}a_{x(t)}=0\\a_{z(t)}=-g\end{pmatrix}$$

Or
$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$

On intègre le système d’équation précédent :
$$\overrightarrow{v}\begin{pmatrix}v_{x(t)}=C_1\\v_{z(t)}=-gt+C_2\end{pmatrix}$$

Pour trouver les constantes, on utilise $\overrightarrow{v}_0$
$$\overrightarrow{v}_0\begin{pmatrix}v{0x}=v_0\cos\alpha\\v{0z}=v_0\sin\alpha\end{pmatrix}$$

D’ou
$$\overrightarrow{v}\begin{pmatrix}v_{x(t)}=v_0\cos\alpha\\v_{z(t)}=-gt+v_0\sin\alpha\end{pmatrix}$$

Or
$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$

On intègre le système d’équation précédent :
$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0\cos(\alpha)\times t+C_3\\z(t)=-\frac{1}{2}gt^2+v_0\sin(\alpha)\times t+C_4\end{pmatrix}$$

Pour trouver les constantes, on utilise $\overrightarrow{OG}_0$
$$\overrightarrow{OG}_0\begin{pmatrix}x_0=0\\z_0=h\end{pmatrix}$$

d’ou

$$\overrightarrow{OG}\begin{pmatrix}x(t)=v_0\cos(\alpha)\times t\\z(t)=-\frac{1}{2}gt^2+v_0\sin(\alpha)\times t+h\end{pmatrix}$$

3. Vérifier que le vol du ballon, jusqu’à ce qu’il touche le sol, dure 3,97 s.

Le vol du ballon jusqu’à ce qu’il touche le sol est le temps pour lequel $z=0$
Il faut lire $v_0=20,5\ m.s^{-1}$ et non $v_0=20,5\ km.h^{-1}$ on retrouve 3,97s.
$$z(t_{sol})=-\frac{1}{2}g{t_{sol}}^2+v_0\sin(\alpha)\times t_{sol}+h$$
$$0=-\frac{1}{2}\times 9,81\times {t_{sol}}^2+20,5\sin(70)\times t_{sol}+90\times {10}^{-2}$$
$$0=-4,905\times {t_{sol}}^2+19,26\times t_{sol}+9,0\times {10}^{-1}$$

C’est une équation du second degré :
$$\Delta=b^2-4ac$$
$$\Delta=(19,26)^2-4\times -4,905\times 9,0\times {10}^{-1}$$
$$\Delta=371$$
$$t_{sol1}=\frac{-b+\sqrt{\Delta}}{2a}$$
$$t_{sol1}=\frac{-(19,26)+\sqrt{371}}{2\times -4,905}$$
$$t_{sol1}=-1,39\times {10}^{-4}\ s$$
Or $t$ est positif
$$t_{sol2}=\frac{-b-\sqrt{\Delta}}{2a}$$
$$t_{sol2}=\frac{-(19,26)-\sqrt{371}}{2\times -4,905}$$
$$t_{sol2}=3,94\ s$$

Une chandelle est réussie si le joueur de rugby qui a tapé le ballon le récupère. Lors de sa chandelle, le joueur saute et parvient à récupérer son ballon au bout de 3,82 s.

4. Calculer l’altitude du ballon lorsque le joueur le récupère.

Calculons l’altitude (z) du ballon lorsque le joueur le récupère (au bout de 3,82 s).
$$z(t)=-\frac{1}{2}gt^2+v_0\sin(\alpha)\times t+h$$
$$z(t=3,82)=-\frac{1}{2}\times 9,81\times {3,82}^2+20,5\sin(70)\times 3,82+90\times {10}^{-2}$$
$$z(t=3,82)=2,9\ m$$

Lors de la coupe du monde 2023, le talonneur Julien Marchand a tapé le ballon, puis a sprinté vers le ballon avec une vitesse moyenne de 25,7 km·h^–1.

5. Déterminer si Julien Marchand aurait été capable de réussir la chandelle étudiée dans les questions précédentes (chandelle du joueur de rugby précédent avec les mêmes caractéristiques).

Julien Marchand a tapé le ballon, puis a sprinté vers le ballon avec une vitesse moyenne de 25,7 km·h^–1

Méthode 1 :
Calculons la distance horizontale parcourue par Julien Marchand en 3,82 s :
$$v=\frac{d}{t}$$
$$\frac{d}{t}=v$$
$$d=v\times t$$
$$d=\frac{25,7}{3,6}\times 3,82$$
$$d=27,3\ m$$

Calculons la distance horizontale parcourue par le ballon en 3,82 s (avec $v_0=20,5\ m.s^{-1}$) :
$$x(t)=v_0\cos(\alpha)\times t$$
$$x(t=3,82)=20,5\times \cos(70)\times 3,82$$
$$x(t=3,82)=26,8\ m$$

La distance horizontale parcourue par Julien Marchand est supérieure à la distance horizontale parcourue par le ballon : Julien Marchand aurait été capable de réussir la chandelle étudiée dans les questions précédentes

Méthode 2 :
Calculons vitesse horizontale du ballon (avec $v_0=20,5\ m.s^{-1}$) :
$$v_{x(t)}=v_0\times \cos\alpha$$
$$v_{x(t)}=20,5\times \cos(70)$$
$$v_{x(t)}=7,0\ m.s^{-1}$$

Calculons vitesse horizontale de Julien Marchand :
$$v=\frac{25,7}{3,6}$$
$$v=7,1\ m.s^{-1}$$

La vitesse horizontale de Julien Marchand est supérieure à la vitesse horizontale de ballon : Julien Marchand aurait été capable de réussir la chandelle étudiée dans les questions précédentes.

Partie B – Étude énergétique d’une chandelle

Par une modélisation numérique, on cherche à calculer la vitesse du ballon lorsqu’il est récupéré par le joueur. Pour cela, on effectue une étude énergétique du système défini dans la partie A à l’aide d’un programme en langage Python dont un extrait est présenté ci- dessous. Ce programme utilise les coordonnées x(t) et z(t) du vecteur position et v_x(t) et v_z(t) du vecteur vitesse obtenues par modélisation de la trajectoire du ballon.

Les variables x, z, vx et vz sont déclarées dans le code mais non affichées dans l’extrait de la figure 2.

…
7	# Déclaration des constantes
8	m = 0.440 # en kg
9	g = 9.81 # en N/kg
…
25	# Calcul des énergies
26	… = (vx2 + vz2)**(1/2)
27	… = 0.5 * m * v**2
28	Ep = ……… # Ep = 0 si z = 0
29	Em = ………

Figure 2 – Extrait du programme écrit en langage Python

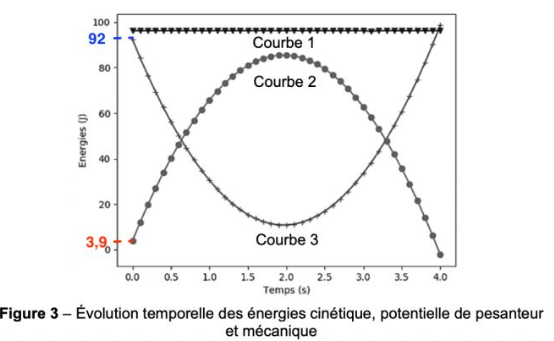
L’exécution de ce programme permet d’obtenir le graphique de la figure 3 page suivante qui modélise l’évolution des énergies du point G au cours du temps.

6. Relever dans le code de la figure 2 la valeur de la masse du ballon.

Dans l’extrait du code Python (figure 2, ligne 8), la masse du ballon est donnée : $m=0.440\ kg$

7. Identifier les grandeurs calculées aux lignes 26 et 27.

Ligne 26 : … = (vx**2 + vz**2)**(1/2)
La grandeur calculée est la vitesse du ballon : $v=\sqrt{v_x^2+v_z^2}$

Ligne 27 : … = 0.5 * m * v**2
La grandeur calculée est l’énergie cinétique du ballon: $E_c=\frac{1}{2}mv^2$

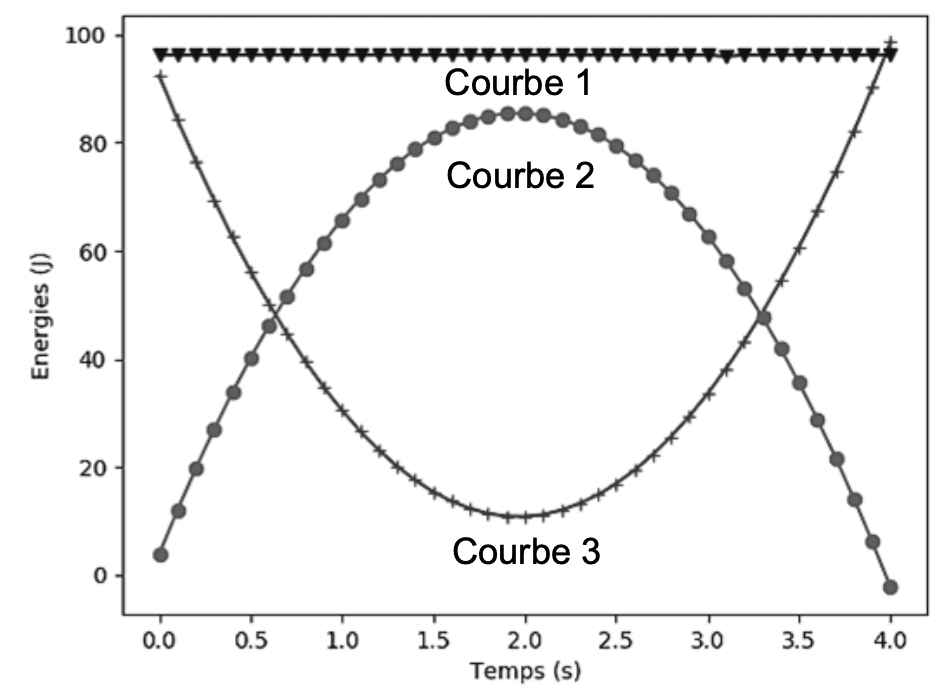
Figure 3 – Évolution temporelle des énergies cinétique, potentielle de pesanteur et mécanique

8. Recopier et compléter le code des lignes 27, 28 et 29 du programme.

Ligne 27 : Ec = 0.5 * m * v**2
Ligne 28 : Ep = m * g * z
Ligne 29 : Em = Ec + Ep

9. En justifiant, attribuer la nature de l’énergie correspondant à chaque courbe du graphique de la figure 3.

$$E_m=E_c+E_p$$
L’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur.
La courbe de l’énergie mécanique est donc au-dessus des courbes de l’énergie cinétique et l’énergie potentielle de pesanteur : courbe 1.

$$E_{pp}=m\times g\times z$$
Calculons l’énergie potentielle de pesanteur à l’instant initial :
$$E_{pp}(0)=m\times g\times z_0$$
$$E_{pp}(0)=m\times g\times h$$
$$E_{pp}(0)=0,440\times 9,81\times 90\times {10}^{-2}$$
$$E_{pp}(0)=3,9\ J$$
L’énergie potentielle de pesanteur initiale est de 3,9 J : Courbe 3

$$E_c=\frac{1}{2}\times m\times v^2$$
Calculons l’énergie cinétique à l’instant initial (avec $v_0=20,5\ m.s^{-1}$) :
$$E_c(0)=\frac{1}{2}\times 0,440\times {20,5}^2$$
$$E_c(0)=92\ J$$
L’énergie cinétique initiale est de 92 J : Courbe 2

10. Indiquer, en expliquant, si l’hypothèse sur les frottements de l’air, proposée au début de l’exercice, a été prise en compte dans la modélisation numérique.

Dans la modélisation numérique, l’énergie mécanique du ballon reste constante au cours du temps. Les frottements de l’air sont donc négligés, conformément à l’hypothèse formulée au début de l’exercice : « les frottements liés à l’action de l’air sont supposés négligeables ».

Le joueur tape le ballon et lui communique une vitesse initiale v0 dont la valeur est celle de la partie A. Il récupère le ballon à une altitude de 2,90 m.

11. À l’aide d’une étude énergétique, calculer la vitesse du ballon, en km·h–1, lorsqu’il est récupéré par le joueur.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti : la démarche est évaluée et nécessite d’être correctement présentée.

D’après le sujet : les frottements liés à l’action de l’air sont supposés négligeables. Ainsi l’énergie mécanique se conserve :
$$E_m(R)=E_m(0)$$
$$\frac{1}{2}\times m\times v_R^2+m\times g\times z_R=\frac{1}{2}\times m\times v_0^2+m\times g\times h$$
$$m\times\left(\frac{1}{2}\times v_R^2+g\times z_R\right)=m\times\left(\frac{1}{2}\times v_0^2+g\times h\right)$$
$$\frac{1}{2}\times v_R^2+g\times z_R=\frac{1}{2}\times v_0^2+g\times h$$
$$\frac{1}{2}\times v_R^2=\frac{1}{2}\times v_0^2+g\times h-g\times z_R$$
$$\frac{1}{2}\times v_R^2=\frac{1}{2}\times v_0^2+g\times\left(h-z_R\right)$$
$$\frac{1}{2}\times v_R^2=\frac{1}{2}\times v_0^2+g\times\left(h-z_R\right)$$
$$v_R^2=v_0^2+2\times g\times\left(h-z_R\right)$$
$$v_R=\sqrt{v_0^2+2\times g\times\left(h-z_R\right)}$$
(avec $v_0=20,5\ m.s^{-1}$) :
$$v_R=\sqrt{{20,5}^2+2\times 9,81\times\left(90\times {10}^{-2}-2,90\right)}$$
$$v_R=19,5\ m.s^{-1}$$
$$v_R=19,5\times 3,6$$
$$v_R=70,2\ km\cdot h^{-1}$$

Lorsqu’il est récupéré par le joueur, la vitesse du ballon est de 70,2 km·h^–1.