La planète mercure

Polynésie 2022 Sujet 2

Exercice B – (5 points) – au choix du candidat – Durée 0h53 – Calculatrice autorisée

Sujet n° 22-PYCJ2P01

Mots-clés : lois de Kepler ; interaction gravitationnelle ; deuxième loi de Newton

Planète la plus proche du Soleil, Mercure est longtemps restée mal connue. En première approximation, sa trajectoire dans le référentiel héliocentrique peut être considérée comme circulaire. Toutefois, de toutes les planètes du Système solaire, c’est celle qui possède l’orbite la plus excentrique. Sa distance au Soleil varie en effet de 0,31 ua à 0,47 ua. La vitesse orbitale de Mercure, qui vaut en moyenne 47 km·s^–1, varie quant à elle entre les valeurs extrêmes 39 km·s^–1 et 59 km·s^–1.

Ce n’est que récemment, entre mars 2011 et avril 2015, que la sonde américaine MESSENGER (MErcury Surface, Space ENvironment, GEochemistry and Ranging) a pu être satellisée autour de Mercure. En complément d’autres informations précieuses, la mission MESSENGER a permis de connaître avec précision la masse de cette planète qui ne possède aucun satellite naturel.

L’objectif de cet exercice est d’étudier le mouvement de Mercure autour du Soleil et le mouvement de MESSENGER autour de Mercure. Dans la première partie, on cherchera à déterminer la période de révolution de Mercure. Dans la seconde partie, on cherchera à préciser la trajectoire de MESSENGER.

Données :

Rayon de Mercure : R_M = 2440 km
Unité astronomique : 1 ua = 1,5×10¹¹ m
Constante universelle de gravitation : G = 6,67×10^–11 m³·kg^–1·s^–2

Étude de la trajectoire de Mercure.

1. Énoncer la première loi de Kepler, dite « loi des orbites ». Représenter, sans souci d’échelle, l’allure de la trajectoire de Mercure autour du Soleil. Le schéma fera apparaître la position du Soleil et le demi-grand axe de l’orbite.

Réponse :

Première loi de Kepler : Dans le référentiel héliocentrique, le centre de chaque planète décrit une trajectoire elliptique dont le soleil S est l’un des foyers.

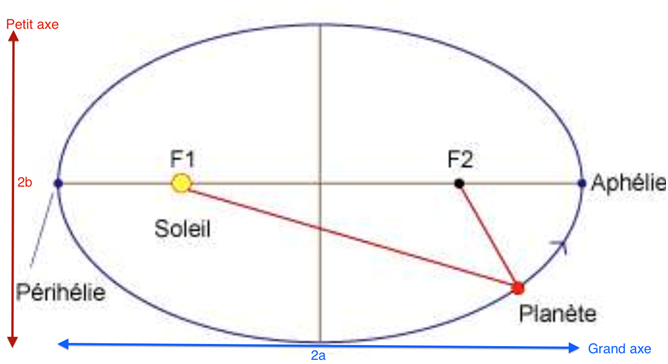
2. En vous appuyant sur le schéma réalisé et sur des informations tirées du texte introductif, montrer par un calcul simple que le demi-grand axe vaut 0,39 ua.

Réponse :

D’après le texte : « sa distance au soleil varie de 0,31 ua à 0,47 ua »

C’est respectivement la distance la plus proche et la plus éloignée.

2a=0,47+0,31

2a=0,78

a=(0,78)/2

a=0,39 ua

3. Énoncer la deuxième loi de Kepler, dite « loi des aires ». Appliquer cette loi pour déterminer dans quelle partie de sa trajectoire Mercure atteint la vitesse de 39 km·s^–1. Une justification claire, pour laquelle le schéma pourra être complété, est attendue.

Réponse :

Deuxième loi de Kepler : loi des aires

Le segment soleil planète balaie des aires égales au cours de durées égales.

Pour que les aires soient égales, il faut que la distance parcourue lorsque la planète est proche soit supérieure à la distance parcourue lorsque la planète est éloignée.

Or le temps de parcours est identique.

Donc la planète va plus vite lorsqu’elle est proche d’un foyer de l’ellipse que quand elle est loin.

Ainsi, pour la plus petite valeur de la vitesse 39 Km.s^-1, mercure se trouve au point le plus éloigné (l’aphélie) soit à une distance de 0,47 ua.

La troisième loi de Kepler est souvent écrite sous la forme : $\frac{T^2}{a^3}=k$ , où la constante de Kepler k évoque le mot allemand « konstante ».

Donnée :

Constante de Kepler pour le Système solaire : k = 2,9×10^–19 s²·m^–3

4. Donner la signification des grandeurs T et a pour Mercure. À l’aide des données utiles et de la troisième loi de Kepler, justifier que cette planète parcourt l’ensemble de son orbite autour du Soleil en un peu moins de trois mois.

Étude de la trajectoire de MESSENGER.

Une fois satellisée autour de Mercure, la sonde MESSENGER a effectué ses orbites avec une période de révolution TS égale à 8,00 heures. Lors de son passage au plus près de la surface de la planète, à l’altitude h égale à 200 km, la sonde possédait une accélération a_S de valeur 3,15 m·s^–2. On supposera que cette accélération était uniquement due à l’attraction gravitationnelle de Mercure.

On rappelle l’expression de la force gravitationnelle exercée par un corps A de masse m_A sur un corps B de masse m_B : $\overrightarrow{F}$ $_A_/_B=\frac{G \cdot m_A \cdot m_B}{r^2}\cdot$ $\overrightarrow{u}$

Dans cette expression, $\overrightarrow{u}$ est un vecteur unitaire orienté de B vers A et r représente la distance entre les centres de masse des corps.

Pour les questions suivantes, on pourra noter m_S la masse de la sonde, M la masse de Mercure et R_M son rayon.

La figure 1 représente la sonde MESSENGER (symbolisée par son centre de masse S) se déplaçant sur une portion de sa trajectoire à l’altitude h.

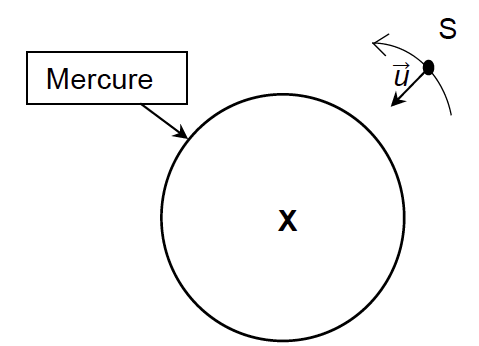
Figure 1 : La sonde MESSENGER passant au plus près de Mercure
(échelle non respectée)

5. Donner la signification des grandeurs T et a pour Mercure. À l’aide des données utiles et de la troisième loi de Kepler, justifier que cette planète parcourt l’ensemble de son orbite autour du Soleil en un peu moins de trois mois.

Reproduire le schéma de la figure 1 pour le compléter en y faisant apparaître sans souci d’échelle :

les distances R_M, h et r ;
le vecteur force gravitationnelle exercée par Mercure sur la sonde $\overrightarrow{F}$ $_M_/_S$ ;
le vecteur vitesse $\overrightarrow{v_S}$ de la sonde ;
le vecteur accélération $\overrightarrow{a_S}$ de la sonde.

Réponse :

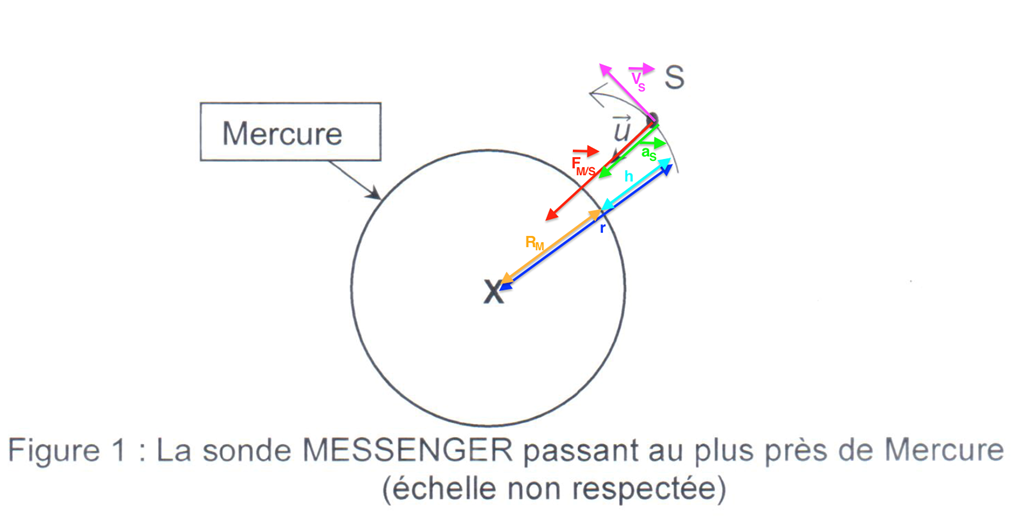
$\overrightarrow{F}_{M/S}$ : La force qu’exerce Mercure sur Messenger est orientée de Messenger vers Mercure.

$\overrightarrow{a}_{S}$ : $\sum_{}^{}\overrightarrow{F_{ext}}=m_{S}\overrightarrow{a}_{S}$ donc à la même direction et le même sens que $\overrightarrow{F}_{M/S}$

$\overrightarrow{v}_{S}$ est tangent à la trajectoire dans le sens du mouvement

6. Énoncer la deuxième loi de Newton, puis l’appliquer au système MESSENGER dans le référentiel mercurocentrique considéré comme galiléen. En déduire l’expression du vecteur accélération $\overrightarrow{a_S}$ de la sonde.

Réponse :

Système : sonde MESSENGER

Référentiel : Mercurocentrique supposé galiléen

D’après la 2^nd loi de Newton :

$\sum_{}^{}\overrightarrow{F_{ext}}=m_{S}\overrightarrow{a}_{S}$

$\overrightarrow{F}_{M/S}=m_{S}\overrightarrow{a}_{S}$

$G\times \frac{m_{S}\times M}{r^2}\overrightarrow{u}=m_{S}\overrightarrow{a}_{S}$

$\overrightarrow{a}_{S}=G\times \frac{M}{r^2}\overrightarrow{u}$

$\overrightarrow{a}_{S}=G\times \frac{M}{\left( R_M+h \right)^2}\overrightarrow{u}$

7. À l’aide des données utiles, montrer que la valeur de l’accélération mesurée à l’altitude h permet d’attribuer à la planète Mercure une masse M égale à 3,29×10²³ kg.

Ses lois de la gravitation et du mouvement ont permis à Newton d’établir l’expression de la constante de Kepler pour tout corps de masse m orbitant autour d’un astre attracteur de masse M (très supérieure à m) : $k=\frac{4 \pi^2}{G \cdot M}$

8. En appliquant la troisième loi de Kepler au mouvement de la sonde MESSENGER autour de Mercure, calculer la valeur du demi-grand axe, a, de son orbite. À l’aide de cette valeur, expliquer pourquoi la trajectoire de la sonde ne peut pas être considérée comme circulaire.