La presbytie

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH107 et n°SPEPHCH115

La presbytie est un défaut de la vision qui apparaît avec l’âge. Généralement autour de 45 ans, il devient difficile de voir net de près. Très souvent, les premiers signes se manifestent lors de la lecture. La personne ne peut plus lire de près et tient son livre ou les objets à distance pour les voir nettement. Ce défaut s’installe naturellement avec le vieillissement du cristallin qui perd en souplesse et en élasticité : on dit alors que l’œil a alors du mal à accommoder. Si plus de 90 % des personnes qui ont besoin d’une correction utilisent des lunettes correctrices, certains patients préfèrent se tourner vers des techniques de chirurgie.

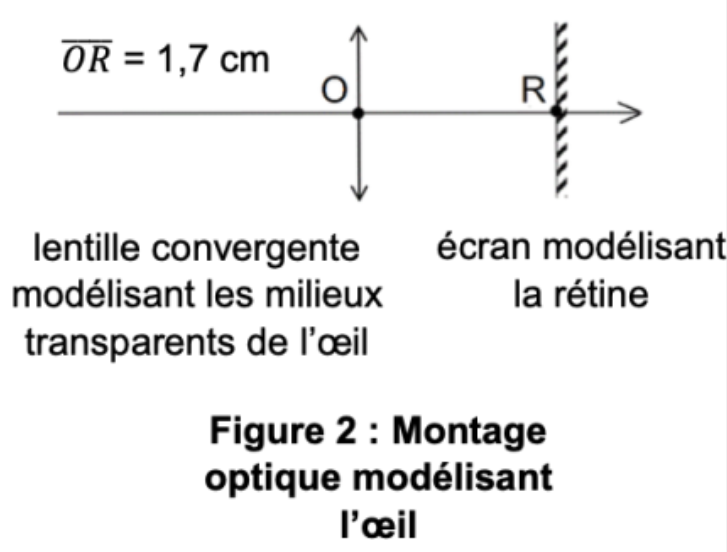
Figure 2 : Montage optique modélisant l’œil

La première partie de l’exercice porte sur la modélisation de l’œil par un montage d’optique et la seconde partie étudie les principes de la correction de la presbytie.

1. Le modèle de l’œil normal Anatomie de l’œil

Dans l’œil, la lumière traverse différents milieux transparents : la cornée, l’humeur aqueuse, le

cristallin et l’humeur vitrée. Pour être vu nettement, l’image de l’objet observé doit se former sur la rétine. La distance cristallin-rétine est fixe.

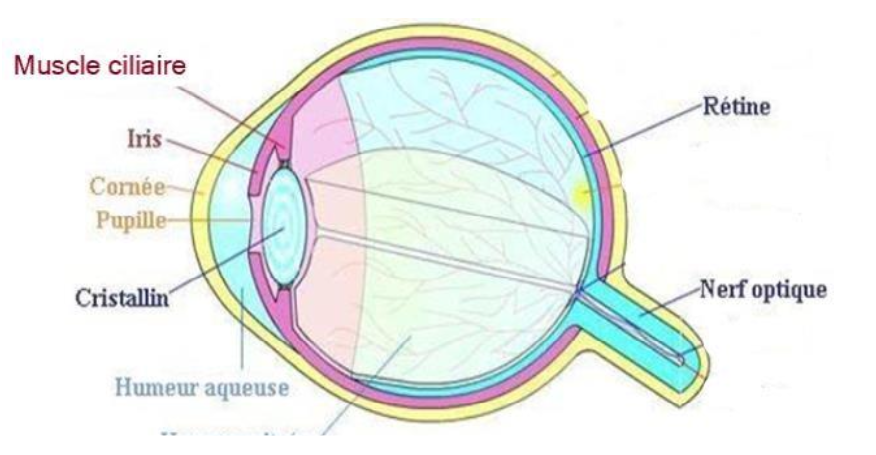
Figure 1 : Représentation schématique simplifiée de l’anatomie de l’œil

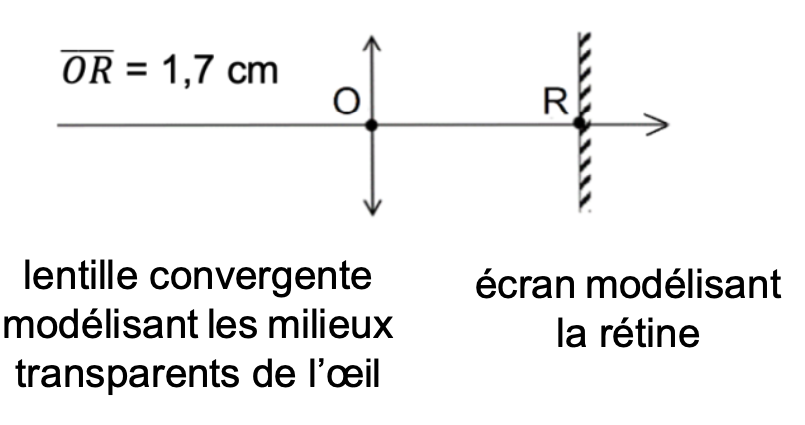
Figure 2 : Montage optique modélisant l’œil

On modélise les différents milieux transparents de l’œil par une lentille mince (L) de centre optique O et la rétine par un écran fixe situé à 1,7 cm de O.

Données :

Relation de conjugaison pour une lentille mince :

$\mathrm{ \frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'} }$

𝑓^′ est la distance focale de la lentille ;

O est le centre optique de la lentille ;

A est un point objet situé sur l’axe optique et A’ est l’image du point A à travers la lentille mince.

La vergence C d’une lentille est égale à l’inverse de sa distance focale ; elle est homogène à l’inverse d’une longueur (cette dernière étant exprimée en mètres) et s’exprime en dioptries (δ) :

$\mathrm{ C = \frac{1}{f'} }$

Lorsque qu’un œil normal (sans défaut) est au repos, il parvient à voir nettement les objets situés à grande distance (« à l’infini ») ; l’image se forme sur la rétine.

1.1. À l’aide de la figure 2, indiquer la position particulière du foyer image de la lentille (L) modélisant l’œil normal lorsqu’il regarde à l’infini. Justifier votre réponse. En déduire la valeur de la distance focale f_a’ de cette lentille (L) et la valeur de sa vergence C_o.

$\mathrm{\frac{1}{\overline{OA'}} - \frac{1}{\overline{OA}} = \frac{1}{f'}}$

Lorsqu’un objet est situé à l’infini : $\overline{OA} = \infty$

$\mathrm{\frac{1}{\overline{OA'}} - \frac{1}{\infty} = \frac{1}{f'}}$

$\mathrm{\frac{1}{\overline{OA'}} - 0 = \frac{1}{f'}}$

$\mathrm{\frac{1}{\overline{OA'}} = \frac{1}{f'}}$

$\mathrm{\overline{OA'} = f'}$

Ainsi, l’image d’un objet à l’infini se trouve sur le foyer image.

Sur la figure 2, l’écran est la rétine.

Pour être vu nettement, l’image de l’objet observé doit se former sur la rétine.

Ainsi, lorsque l’œil normal regarde à l’infini, le foyer image de la lentille (L) se situe au point R sur la rétine.

La distance focale est donc de f_a’=OR=1,7 cm

Calculons la vergence de l’œil :

$\mathrm{ C_0 = \frac{1}{\overline{f_a'}}}$

$\mathrm{ C_0 = \frac{1}{1,7 \times 10^{-2}}}$

$\mathrm{ C_0 = 59 \, \text{d}^\circ}$

Lorsque cet œil normal regarde un objet proche, les muscles ciliaires déforment le cristallin. Celui-ci se bombe pour que l’image se forme toujours sur la rétine. On dit que l’œil accommode. L’œil normal observe maintenant avec netteté un objet AB situé à une « distance » $\overline{OA'}=−20,0 cm.$
Le montage optique modélisant l’œil ainsi que l’objet AB est représenté à l’échelle 1 sur l’ANNEXE À RENDRE AVEC LA COPIE.

1.2. Sur le schéma de l’ANNEXE À RENDRE AVEC LA COPIE, construire l’image A’B’ de l’objet AB à travers la lentille (L). Déduire par construction graphique une estimation de la distance focale f_b’_schéma de la lentille (L).

Le rayon lumineux issu de B pénétrant dans la lunette par le centre optique O de la lentille n’est pas dévié.

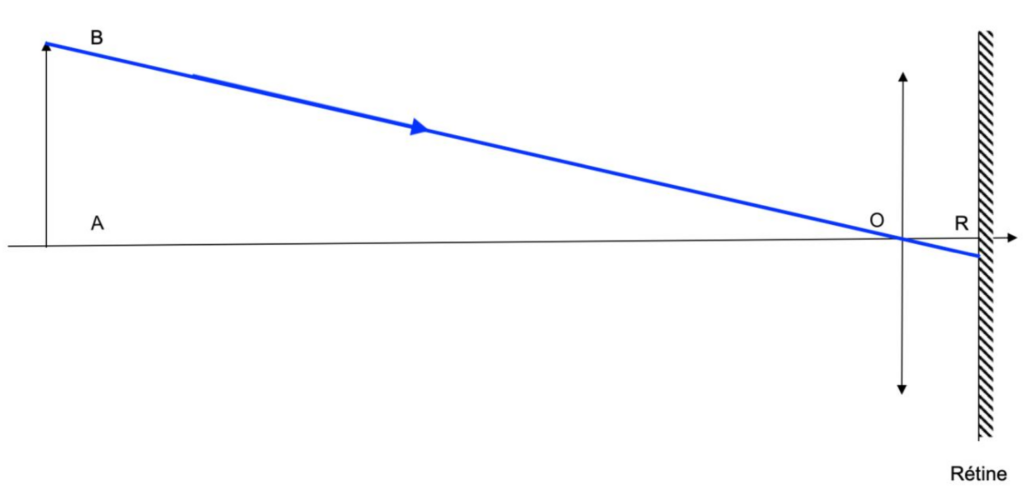
Or, d’après le sujet, pour être vu nettement, l’image de l’objet observé doit se former sur la rétine.

Ainsi, le point B’ est sur la rétine et A’ sur l’axe optique.

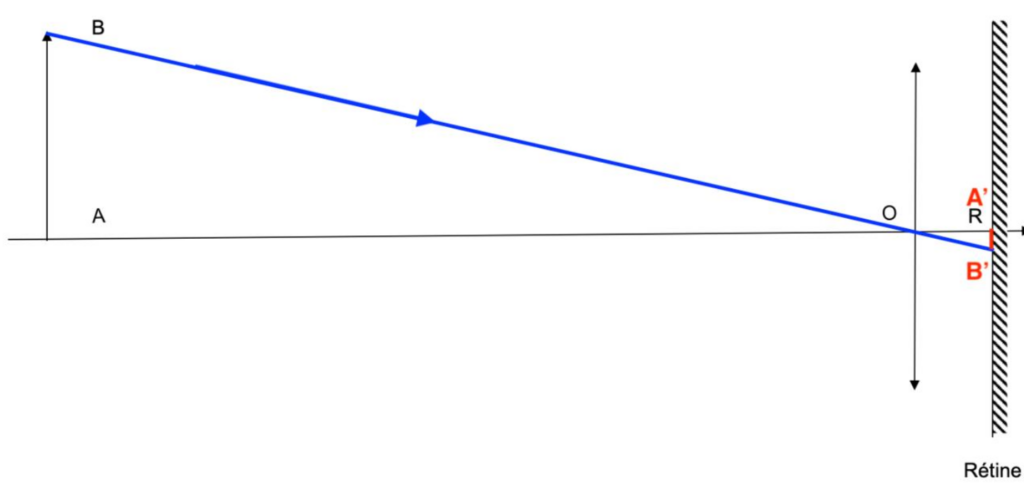
Le rayon lumineux issu de B parallèle à l’axe optique pénétrant dans la lunette est dévié vers B’.

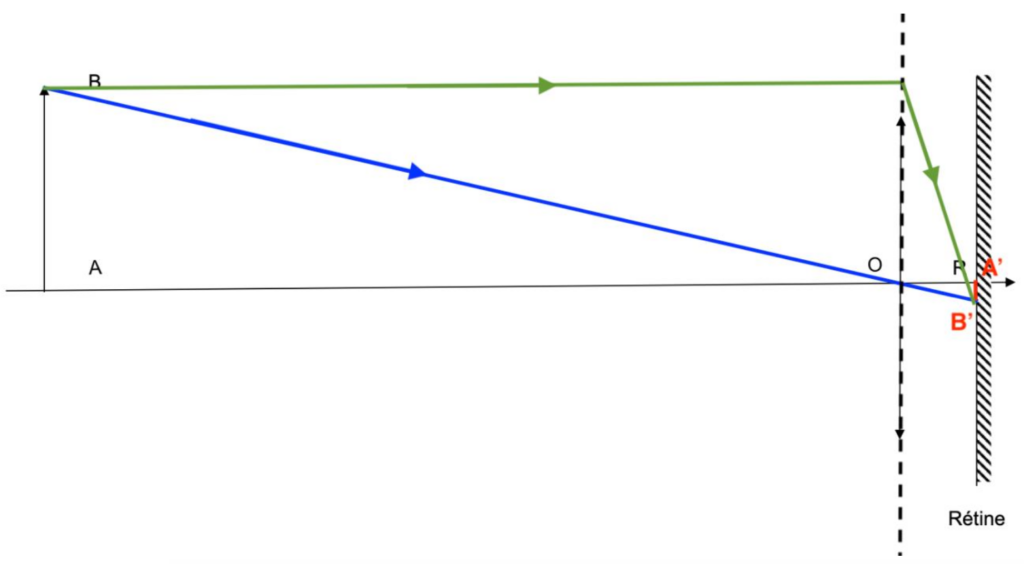
Or Le rayon lumineux issu de B parallèle à l’axe optique pénétrant dans la lunette est dévié en passant par le foyer image F’.

L’intersection de ce rayon et l’axe optique nous donne F’.

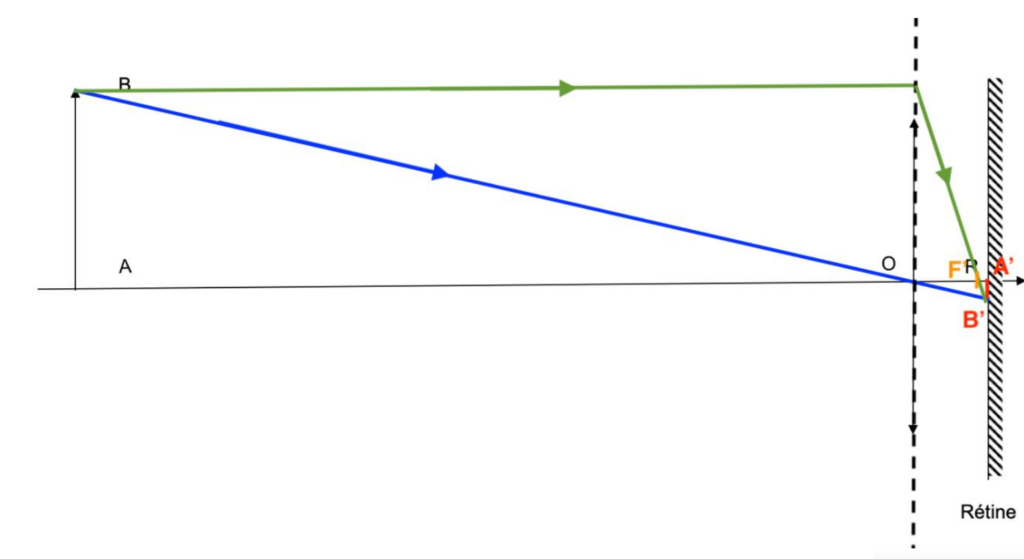
On en déduit une estimation de la distance focale : f_b’_schéma = 1,5 cm

1.3. A l’aide de la relation de conjugaison, déterminer la distance focale f_b’_théoriquede la lentille (L).

$\mathrm{\frac{1}{\overline{OA'} } - \frac{1}{\overline{OA} } = \frac{1}f_b'_{\text{théorique}}}}$

$\mathrm{\frac{1}f_b'_{\text{théorique}}} = \frac{1}{\overline{OA'} } - \frac{1}{\overline{OA} }}$

$\mathrm{\frac{1}f_b'_{\text{théorique}}} = \frac{1 \times \overline{OA}}{\overline{OA'} \times \overline{OA}} - \frac{1 \times \overline{OA'} }{\overline{OA} \times \overline{OA'}}}$

$\mathrm{\frac{1}f_b'_{\text{théorique}}} = \frac{\overline{OA} - \overline{OA'}}{\overline{OA'} \times \overline{OA}}}$

$\mathrmf_b'_{\text{théorique}} = \frac{\overline{OA'} \times \overline{OA}}{\overline{OA} - \overline{OA'}}}$

$\mathrm{ {f_b'}_{\text{théorique}} = \frac{1,7 \times 10^{-2} \times (-20,0 \times 10^{-2})}{-20,0 \times 10^{-2} - 1,7 \times 10^{-2}}}$

$\mathrm{ {f_b'}_{\text{théorique}} = 1,6 \times 10^{-2} \, \text{m}}$

$\mathrm{ {f_b'}_{\text{théorique}} = 1,6 \, \text{cm}}$

1.4. Confronter les résultats f_b’_schéma et f_b’_théorique.

f_b’_schéma =1,5 cm et f_b’_théorique =1,6 cm : les deux résultats sont quasiment identiques.

1.5. L’accommodation réalisée par la déformation du cristallin modifie la distance focale de la lentille (L). Comparer les vergences de l’œil au repos et de l’œil qui accommode.

Calculons la vergence de l’œil qui accommode :

$\mathrm{ C_{\text{acco}} = \frac{1}{\overline{f'_b}}}$

$\mathrm{ C_{\text{acco}} = \frac{1}{1,6 \times 10^{-2}}}$

$\mathrm{ C_{\text{acco}} = 62,5 \, \text{dioptries}}$

Or, au repos,

$\mathrm{ C_0 = 59 \, \text{dioptries}}$

Ainsi,

$\mathrm{ C_{\text{acco}} > C_0}$

La vergence de l’œil au repos est inférieure à celle de l’œil qui accommode.

2. Presbytie et lunettes correctrices

Avec l’âge, le cristallin perd en souplesse. Les muscles ciliaires ne parviennent plus à bomber suffisamment le cristallin. L’œil peine donc à faire une mise au point quand il observe un objet proche de lui. Il perd progressivement son pouvoir d’accommodation, la presbytie s’installe. La vergence de l’œil presbyte au repos reste identique à celle de l’œil normal. Cependant, elle ne peut plus varier suffisamment pour voir nettement les objets de près.

Une personne souffrant de presbytie accommode légèrement de telle sorte que la vergence C₁ de la lentille modélisant les milieux transparents de son œil ne peut atteindre que la valeur C₁ = 61 δ.

2.1. Dans ces conditions d’accommodation et en utilisant la relation de conjugaison (voir données partie 1), déterminer la valeur de la distance à laquelle cette personne peut voir net un objet. On rappelle que la distance OR reste constante : OR = 1,7 cm (figure 2 de la partie 1).

Nous avons :

$\mathrm{\frac{1}{\overline{OA'} } - \frac{1}{\overline{OA} } = \frac{1}{f'}}$

Or,

$\mathrm{C_1 = \frac{1}{f'}}$

Et,

$\mathrm{\overline{OA'} = \overline{OR}}$

D’où,

$\mathrm{\frac{1}{\overline{OR}} - \frac{1}{\overline{OA}} = C_1}$

$\mathrm{-\frac{1}{\overline{OA}} = C_1 - \frac{1}{\overline{OR}}}$

$\mathrm{\frac{1}{\overline{OA}} = -C_1 + \frac{1}{\overline{OR}}}$

$\mathrm{\frac{1}{\overline{OA}} = \frac{-C_1 \times \overline{OR} + 1}{\overline{OR}}}$

$\mathrm{\overline{OA} = \frac{\overline{OR}}{-C_1 \times \overline{OR} + 1}}$

En utilisant les valeurs,

$\mathrm{\overline{OA} = \frac{1,7 \times 10^{-2}}{-61 \times 1,7 \times 10^{-2} + 1}}$

$\mathrm{\overline{OA} = -0,46 \, \text{m}}$

$\mathrm{\overline{OA} = -46 \, \text{cm}}$

La distance à laquelle cette personne peut voir net un objet est de 46 cm.

Pour corriger sa presbytie, le médecin ophtalmologiste prescrit à cette personne des lunettes pour voir de près. Le port de ces lunettes correctrices permet au patient de voir de près en accommodant légèrement. En vision de près, la vergence du dispositif optique {œil+lunettes} est alors égale à C = 62,5 δ.

Donnée :

Si on associe deux lentilles minces séparées par une distance négligeable et de vergences respectives C₁ et C₂, le système est alors assimilable à une lentille unique de vergence C telle que : C = C₁ + C₂.

2.2. Déterminer la valeur de la vergence C₂ des lunettes correctrices portées par le patient en supposant pour simplifier que pour chaque œil la distance du centre optique de chacun de l’œil au verre de lunette est négligeable (ce qui en pratique n’est pas le cas).

C = C₁+ C₂

C₁ + C₂ = C

C₂ = C – C₁

C₂ = 62,5 – 61

C₂ = 1,5 δ

2.3. Justifier que le port de ces lunettes n’est pas conseillé pour voir nettement un objet à l’infini.

Calculons $\overline{(OA')}$ :

$\frac{1}{\overline{(OA')}} - \frac{1}{\overline{(OA)}} = \frac{1}{f'}$

Lorsqu’un objet est situé à l’infini : $\overline{(OA)} = \infty$

$\frac{1}{\overline{(OA')}} - \frac{1}{\infty} = \frac{1}{f'}$

$\frac{1}{\overline{(OA')}} - 0 = \frac{1}{f'}$

$\frac{1}{\overline{(OA')}} = \frac{1}{f'}$

$\overline{(OA')} = f'$

$\overline{(OA')} = \frac{1}{C}$

$\overline{(OA')} = \frac{1}{62,5}$

$\overline{(OA')} = 1,6 \times 10^{-2} \, \text{m}$

$\overline{(OA')} = 1,6 \, \text{cm}$

Or $\overline{(OR)} = 1,7 \, \text{cm}$

Ainsi, avec le port de ces lunettes, l’image d’un objet à l’infini se forme avant la rétine.

L’image ne sera donc pas nette.

C’est pourquoi, le port de ces lunettes n’est pas conseillé pour voir nettement un objet à l’infini.

3. Correction de la presbytie par une chirurgie laser

Une nouvelle technique de chirurgie de l’œil presbyte est à l’étude : la technique « femtoseconde ».

La technique agit directement sur l’acteur principal responsable du phénomène de perte d’accommodation, le cristallin. Elle consiste à pratiquer des incisions sur ce dernier, grâce à un laser femtoseconde. Ce laser émet des impulsions de l’ordre de 500 femtosecondes (fs).

L’énergie délivrée à chaque impulsion est modeste, de l’ordre de E = 0,1 μJ, ce qui permet d’éviter les effets thermiques.

La longueur d’onde des rayonnements émis est λ = 1,0 μm.

Données :

célérité de la lumière dans le vide : c = 3,00 × 10⁸ m.s^-1 ;
constante de Planck : h = 6,63 × 10^–34 J.s ;
l’énergie E d’une impulsion (en J) s’exprime en fonction de la puissance P (en W) d’un laser et la durée τ de l’impulsion (en s) par la relation : 𝐸 = 𝑃 × 𝜏 ;
1 fs = 10^-15 s ;
nombre d’étoiles dans notre Galaxie : entre 200 et 400 milliards ;

Une femtoseconde correspond à un millionième de milliardième de seconde ! Pourtant, le nombre de photons émis lors de chaque impulsion est de l’ordre de grandeur du nombre d’étoiles présentes dans notre Galaxie !

3.1. Vérifier l’affirmation ci-dessus.

Une femtoseconde correspond à un millionième de milliardième de seconde !

$1 \times 10^{-6} \times 1 \times 10^{-9} = 1 \times 10^{-15} \, \text{s} = 1 \, \text{fs}$

Le nombre de photons émis lors de chaque impulsion est de l’ordre de grandeur du nombre d’étoiles présentes dans notre Galaxie !

Énergie d’un photon :

$E = \frac{h \times c}{\lambda}$

$E = \frac{6{,}63 \times 10^{-34} \times 3{,}00 \times 10^{8}}{1{,}0 \times 10^{-6}}$

$E = 2{,}0 \times 10^{-18} \, \text{J}$

Calculons le nombre de photons émis lors de chaque impulsion :

$\mathrm{N = \frac{0{,}1 \times 10^{-6} \times 1}{2{,}0 \times 10^{-18}}}$

$\mathrm{N = 5 \times 10^{10} \text{ photons}}$

Ordre de grandeur : $10^{11} \text{ photons}$

Nombre d’étoiles dans notre Galaxie : entre 200 et 400 milliards ;

$\mathrm{200 \times 10^9 < N_{\text{étoile}} < 400 \times 10^9}$

$\mathrm{2{,}00 \times 10^{11} < N_{\text{étoile}} < 4{,}00 \times 10^{11}}$

Ordre de grandeur : $10^{11} \text{ étoiles}$

Ainsi, l’affirmation « Le nombre de photons émis lors de chaque impulsion est de l’ordre de grandeur du nombre d’étoiles présentes dans notre Galaxie ! » est vérifiée.

3.2. La brièveté des impulsions laser délivrées par le laser femtoseconde permet d’atteindre des puissances très élevées, malgré une énergie délivrée modeste. Expliquer cette affirmation en vous appuyant éventuellement sur un calcul.

$\mathrm{ E = P \times \tau}$

$\mathrm{ P \times \tau = E}$

$\mathrm{ P = \frac{E}{\tau}}$

La puissance est inversement proportionnelle au temps. Ainsi, la brièveté des impulsions (temps petit) laser délivrées par le laser femtoseconde permet d’atteindre des puissances très élevées, malgré une énergie délivrée modeste.

Calculons cette puissance :

$\mathrm{ P = \frac{0{,}1 \times 10^{-6}}{500 \times 10^{-15}}}$

$\mathrm{ P = 2{,}0 \times 10^{5} \text{ W}}$

Effectivement, on trouve une puissance très élevée, malgré une énergie délivrée modeste.

ANNEXE À RENDRE AVEC LA COPIE – Question 1.2

$\text{1 photon}$	$2{,}0 \times 10^{-18} \text{ J}$
$\text{N photons}$	$0{,}1 \text{ μJ} = 0{,}1 \times 10^{-6} \text{ J}$