La protonthérapie sauve la vue

Bac Polynésie 2024 Sujet 1

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°24-PYCJ1PO1

EXERCICE 2 – LA PROTONTHÉRAPIE SAUVE LA VUE (5 POINTS)

Le cyclotron isochrone Medicyc de Nice, est un accélérateur de particules pionnier dans le traitement des cancers par protonthérapie.

Cette technique de médecine nucléaire très précise, accélère des protons leur permettant d’atteindre à leur sortie, une énergie cinétique suffisante pour pénétrer l’œil jusqu’à la rétine comme représenté sur la figure 1.

Ils déposent alors avec précision cette grande quantité d’énergie sur la tumeur rétinienne cible qui est détruite, tout en épargnant les tissus sains et le nerf optique. La vue du patient est sauvée !

Sources : Dans l’oeil du cyclotron-Pierre Mandrillon 2016

L’objectif de cet exercice est de décrire le mouvement d’un proton dans les différentes zones du cyclotron.

Données :

• Un cyclotron est constitué des zones B et C qui sont des cavités semi-circulaires de rayon R_max = 69 cm, séparées par un intervalle étroit qui correspond à la zone A.
• Un cyclotron est un accélérateur de particules qui utilise l’action successive d’un champ électrique $\overrightarrow{E}$ (dans la zone A) et d’un champ magnétique $\overrightarrow{B}$ (dans les zones B et C).

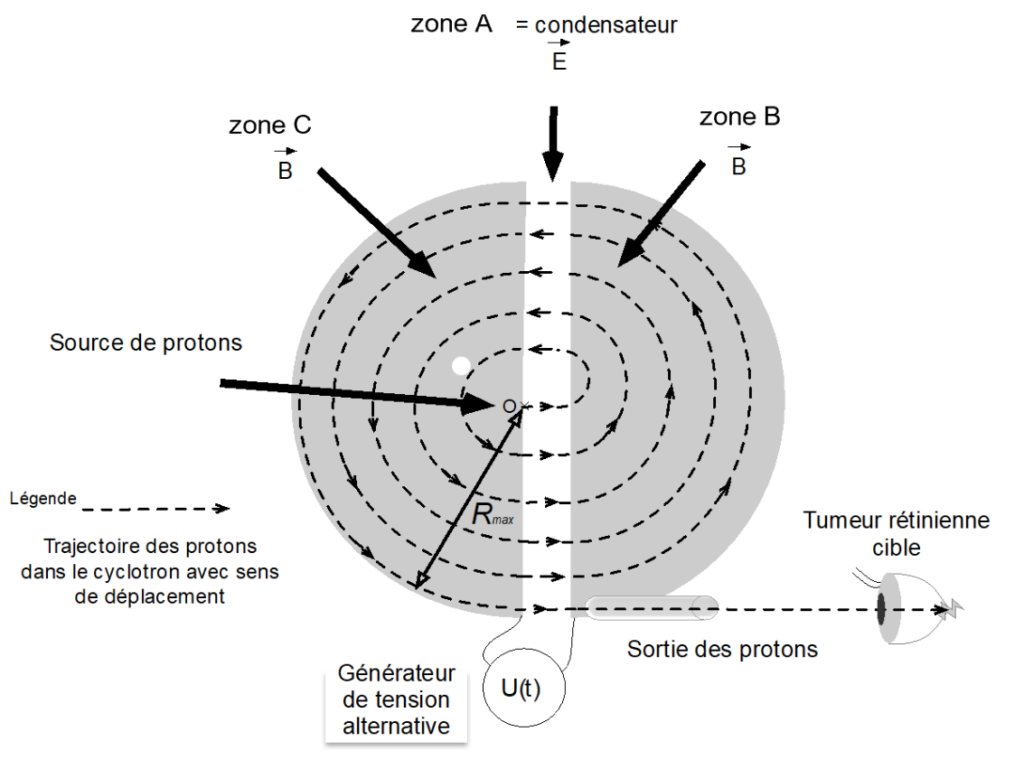
Figure 1. Vue de dessus des zones du cyclotron.

Dans le cadre de l’exercice on supposera que le proton étudié est injecté au point O sans vitesse initiale, et suit les lois de Newton.

Mouvement du proton dans la zone A de O à M₁.

La zone A, est modélisée par un condensateur plan alimenté par une tension U(t) alternative, figure 2.

Il y règne un champ électrique $\overrightarrow{E}$ uniforme, qui a pour valeur :

$$E=\frac{|U|}{d}$$

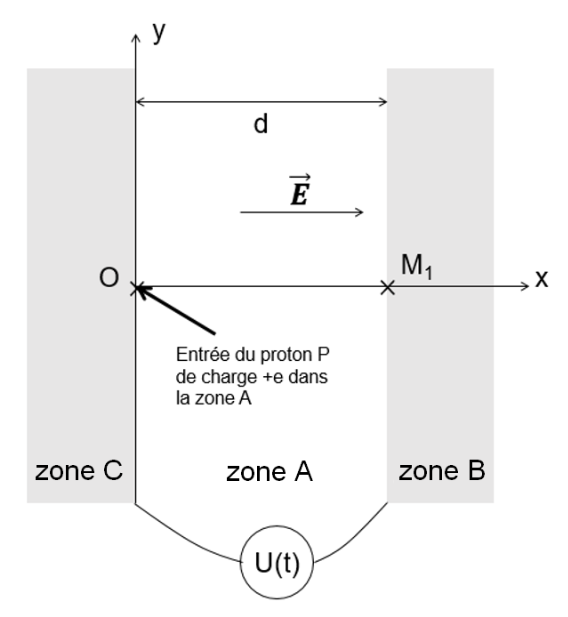
Figure 2. Modélisation de la zone A du cyclotron par un condensateur plan.

Données :

• Charge électrique du proton : e = 1,6 × 10^–19 C ;
• Le poids du proton est négligeable devant la force électrique ;
• Masse du proton : m = 1,67 × 10^–27 kg ;
• La largeur de la zone A est : d = 1,0 cm ;
• Le repère d’étude dans la zone A est le repère (O,x,y) ;
• Unité d’énergie : 1 eV = 1,6 × 10^–19 J ;
• Tension appliquée dans la zone A : U = 50 kV.

Q1. En appliquant la deuxième loi de Newton, déterminer l’expression du vecteur accélération $\overrightarrow{a}$ du proton dans la zone A, en fonction de e, m et $\overrightarrow{E}$, et en déduire ses caractéristiques : direction, sens et valeur. Conclure quant à la nature du mouvement du proton dans la zone A.

Q2. Établir la coordonnée $v_x(t)$ du proton dans le repère (O,x,y) et montrer, avec la méthode de votre choix, que la valeur du vecteur vitesse $\overrightarrow{v_1}$ du proton au point M$_1$, a pour expression : $v_1=v_x(t_1)=\sqrt{\frac{2e\cdot U}{m}}$.

D’ou

$$\overrightarrow{a}\ \left|\begin{matrix}a_{x(t)}=\frac{e}{m}\times E\\ a_{y\left(t\right)}=\frac{e}{m}\times 0\end{matrix}\right.$$
$$\overrightarrow{a}\ \left|\begin{matrix}a_{x(t)}=\frac{e}{m}\times E\\ a_{y\left(t\right)}=0 \end{matrix}\right.$$

$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{v}\ \left|\begin{matrix}v_{x\left(t\right)}=\frac{e}{m}\times E\times t+C_1\\{\ v}_{y\left(t\right)}=C_2 \end{matrix}\right.$$

Pour trouver les constantes, on utilise ${\overrightarrow{v}}0$ (À t= 0, un proton entre dans la zone A, en O, sans vitesse initiale.)
$${\overrightarrow{v}}0\ \left|\begin{matrix}v{0x}=0\\ \v{0z}=0\ \end{matrix}\right.$$

d’ou
$$\overrightarrow{v}\ \left|\begin{matrix}v_{x\left(t\right)}=\frac{e}{m}\times E\times t\\{\ v}_{y\left(t\right)}=0 \end{matrix}\right.$$

Ainsi : $v_{x\left(t\right)}=\frac{e}{m}\times E\times t$

Méthode 1 (un peu longue) :
$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$

On intègre le système d’équation précédent :
$$\overrightarrow{OG}\left|\begin{matrix}x\left(t\right)=\ \frac{1}{2}\times \frac{e}{m}\times E\times t^2\ +C_3\ \\y\left(t\right)=C_4 \end{matrix}\right.$$

Pour trouver les constantes, on utilise ${\overrightarrow{OG}}_0$ (À t= 0, un proton entre dans la zone A, en O.)
$${\overrightarrow{OG}}_0\ \left|\begin{matrix}x_0=0\\ y_0=0\ \end{matrix}\right.$$
d’ou
$$\overrightarrow{OG}\left|\begin{matrix}x\left(t\right)=\ \frac{1}{2}\times \frac{e}{m}\times E\times t^2\ \\y\left(t\right)=0 \end{matrix}\right.$$

Isolons t :
$$x\left(t\right)=\ \frac{1}{2}\times \frac{e}{m}\times E\times t^2$$
$$\frac{1}{2}\times \frac{e}{m}\times E\times t^2=x\left(t\right)$$
$$t^2=\frac{2\times m\times x\left(t\right)}{e\times E}$$
$$t=\sqrt{\frac{2\times m\times x\left(t\right)}{e\times E}}$$

Remplaçons t dans vx :
$$v_{x\left(t\right)}=\frac{e}{m}\times E\times t$$
$$v_{x\left(t\right)}=\frac{e}{m}\times E\times \sqrt{\frac{2\times m\times x\left(t\right)}{e\times E}}$$
$$v_{x\left(t\right)}=\sqrt{\frac{e^2}{m^2}\times E^2\times \frac{2\times m\times x\left(t\right)}{e\times E}}$$
$$v_{x\left(t\right)}=\sqrt{\frac{e}{m}\times E\times 2\times x\left(t\right)}$$
Or
$$E=\frac{\left|U\right|}{d}$$
$$v_{x\left(t\right)}=\sqrt{\frac{e}{m}\times \frac{\left|U\right|}{d}\times 2\times x\left(t\right)}$$

Au point M1, $x_1=d$
$$v_{x1}=v_{x\left(t_1\right)}=\sqrt{\frac{e}{m}\times \frac{\left|U\right|}{d}\times 2\times d}$$
$$v_{x1}=v_{x\left(t_1\right)}=\sqrt{\frac{e}{m}\times \left|U\right|\times 2}$$
$$v_{x1}=v_{x\left(t_1\right)}=\sqrt{\frac{2eU}{m}}$$

Méthode 2 (plus rapide) :
Théorème de l’énergie cinétique : La variation d’énergie cinétique entre deux points O et M1 est égale à la somme des travaux des forces :
$$\Delta E_C=\Sigma W_{OM_1}(\overrightarrow{F})$$
$$E_{C\ finale}-E_{C\ initiale}=W_{OM_1}(\overrightarrow{F})$$
$$E_C\left(M_1\right)-E_C\left(0\right)=\overrightarrow{F}\cdot \overrightarrow{OM_1}$$
$$\frac{1}{2}\times m\times v_1^2-\frac{1}{2}\times m\times v_0^2=q\times \overrightarrow{E}\cdot \overrightarrow{OM_1}$$
À t= 0, un proton entre dans la zone A, en O, sans vitesse initiale.
$$\frac{1}{2}\times m\times v_1^2-0=e\times \overrightarrow{E}\cdot \overrightarrow{OM_1}$$
$$\frac{1}{2}\times m\times v_1^2=e\times E\times OM_1\times \cos(\alpha)$$
$$\frac{1}{2}\times m\times v_1^2=e\times E\times OM_1\times \cos(0)$$
$$\frac{1}{2}\times m\times v_1^2=e\times E\times OM_1\times 1$$
$$\frac{1}{2}\times m\times v_1^2=e\times \frac{U}{d}\times OM_1$$
Or $OM_1=d$
$$\frac{1}{2}\times m\times v_1^2=e\times U$$
$$v_1^2=\frac{2\times e\times U}{m}$$
$$v_1=\sqrt{\frac{2\times e\times U}{m}}$$

Q3. En déduire les caractéristiques, direction, sens et valeur, du vecteur vitesse $\overrightarrow{v_1}$ au point M₁.

$$v_1=\sqrt{\frac{2\times e\times U}{m}}$$

$$v_1=\sqrt{\frac{2\times 1,6\times {10}^{-19}\times 50\times {10}^3}{1,67\times {10}^{-27}}}$$
$$v_1=3,1\times {10}^6\ m.s^{-1}$$

$$\overrightarrow{v}\ \left|\begin{matrix}v_{x\left(t\right)}=\frac{e}{m}\times E\times t\\ {\ v}_{y\left(t\right)}=0 \end{matrix}\right.$$

Caractéristiques du vecteur vitesse ${\overrightarrow{v}}_1$:
Direction : horizontale (selon l’axe Ox)
Sens : vers la droite (sens de l’axe Ox)
Valeur : $v_1=3,1\times {10}^6\ m.s^{-1}$

Mouvement du proton dans la zone B de M₁ à N₁.

Le proton atteint la zone B au point M$_1$, avec la vitesse $\overrightarrow{v_1}$ où règne uniquement un champ magnétique $\overrightarrow{B}$ uniforme, figure 3. Il est soumis à une force magnétique $\overrightarrow{F_m}$ ainsi qu’à son poids.

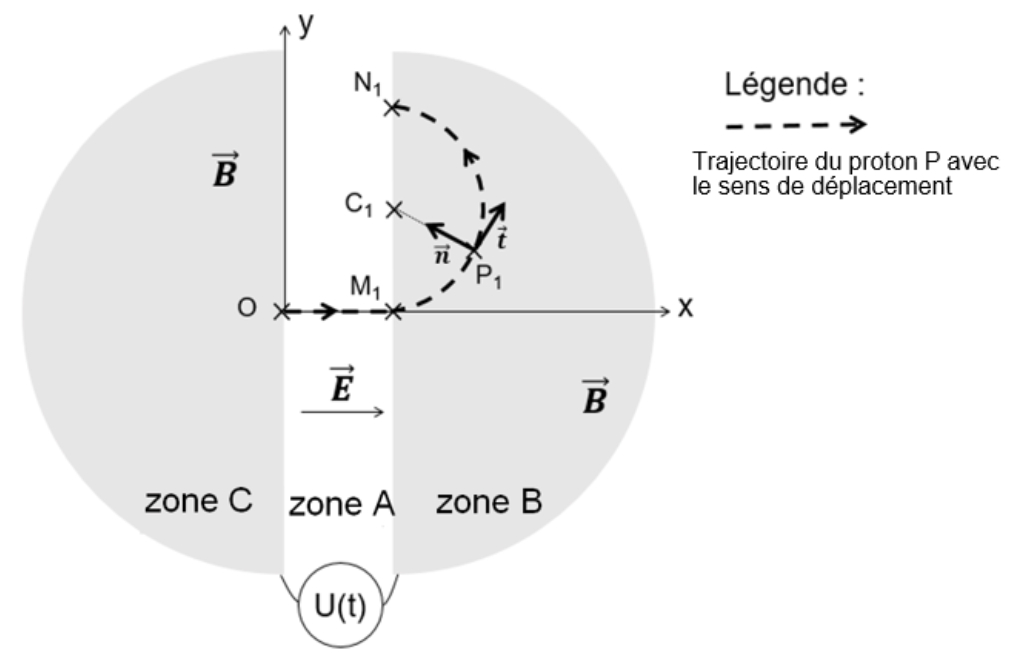
Figure 3. Trajectoire du proton dans les zones A et B du cyclotron.

Données :

• La trajectoire du proton dans la zone B est circulaire, il parcourt un demi-cercle de rayon : R₁ = C₁P₁ = 1,9 cm ;
• Le repère d’étude pour la zone B est le repère de Frenet $(P_1,\overrightarrow{t},\overrightarrow{n})$ ;
• Force du champ magnétique uniforme sur le proton : $\overrightarrow{F_m}=(e\cdot v\cdot B)\ \overrightarrow{n}$ où $\overrightarrow{n}$ est le vecteur du repère de Frenet $(P_1,\overrightarrow{t},\overrightarrow{n})$ ;
• Vecteur accélération dans la base de Frenet : $\overrightarrow{a}=\frac{dv}{dt}\ \overrightarrow{t}+\frac{v^2}{R}\ \overrightarrow{n}$ ;
• Dans la zone B, le champ magnétique a une valeur constante : B = 1,7 T où T est le symbole du tesla, unité de champ magnétique ;
• On néglige le poids du proton devant la force magnétique.

Q4. En utilisant la deuxième loi de Newton, établir l’expression littérale du vecteur accélération $\overrightarrow{a}$ du proton en P₁ et donner ses caractéristiques : direction et sens.

D’après l’énoncé : le proton est soumis à une force magnétique Fm ainsi qu’à son poids.

Système {proton}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{F_m}+\overrightarrow{P}=m\overrightarrow{a}$$
Or d’après les données : nn néglige le poids du proton devant la force magnétique.
$$\overrightarrow{F_m}=m\overrightarrow{a}$$
$$m\overrightarrow{a}=\overrightarrow{F_m}$$
$$\overrightarrow{a}=\frac{\overrightarrow{F_m}}{m}$$

Or d’après les données :
$$\overrightarrow{F_m}=\left(e\times v\times B\right)\times \overrightarrow{n}$$

$$\overrightarrow{a}=\frac{\left(e\times v\times B\right)\times \overrightarrow{n}}{m}$$
$$\overrightarrow{a}=\frac{\left(e\times v\times B\right)}{m}\times \overrightarrow{n}$$

Caractéristiques du vecteur accélération :
Direction. Même direction que $\overrightarrow{n}$ : radiale
Sens. Même sens que $\overrightarrow{n}$ : centripète

Q5. Montrer que le mouvement circulaire du proton est uniforme et établir que l’expression de la valeur de sa vitesse est : $v=\frac{e\cdot R_1\cdot B}{m}$.

D’après les données :
$$\overrightarrow{a}=\frac{dv}{dt}\overrightarrow{t}+\frac{v^2}{R}\overrightarrow{n}$$

Or, d’après la question précédente Q4 :

$$\overrightarrow{a}=\frac{\left(e\times v\times B\right)}{m}\times \overrightarrow{n}$$

L’accélération étant unique, par identification :
$$\frac{v^2}{R}=\frac{\left(e\times v\times B\right)}{m}$$
$$\frac{v}{R}=\frac{e\times B}{m}$$
$$v=\frac{e\times R\times B}{m}$$

Dans notre cas R=R1 :
$$v=\frac{e\times R_1\times B}{m}$$

Q6. Calculer la valeur de la vitesse v et expliquer pourquoi on retrouve la valeur v₁ de la question Q3.

$$v=\frac{e\times R_1\times B}{m}$$
$$v=\frac{1,6\times {10}^{-19}\times 1,9\times {10}^{-2}\times 1,7}{1,67\times {10}^{-27}}$$
$$v=3,1\times {10}^6\ m.s^{-1}$$

D’après les données :
$$\overrightarrow{a}=\frac{dv}{dt}\overrightarrow{t}+\frac{v^2}{R}\overrightarrow{n}$$

Or, d’après la question précédente Q4 :

$$\overrightarrow{a}=\frac{\left(e\times v\times B\right)}{m}\times \overrightarrow{n}$$

L’accélération étant unique, par identification :
$$\frac{dv}{dt}=0$$

Ainsi, la valeur de la vitesse v est constante, c’est pourquoi on retrouve la valeur v1 de la question Q3. Retour du proton dans la zone A puis entrée dans la zone C.

Retour du proton dans la zone A puis entrée dans la zone C.

Le proton quitte la zone B et revient dans la zone A en N₁. Pendant que le proton était dans la zone B, le signe de la tension U(t) a changé pour inverser le sens du champ

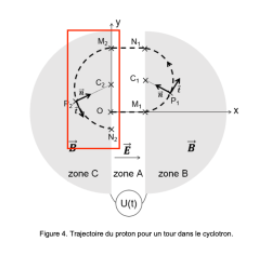
$\overrightarrow{E}$, ce qui lui permet de subir une nouvelle accélération jusqu’au point M₂. Il entre dans la zone C, où il décrit un demi-cercle de rayon C₂P₂ = R₂ tel que : R₂ > R₁, pour en ressortir en N₂, figure 4.

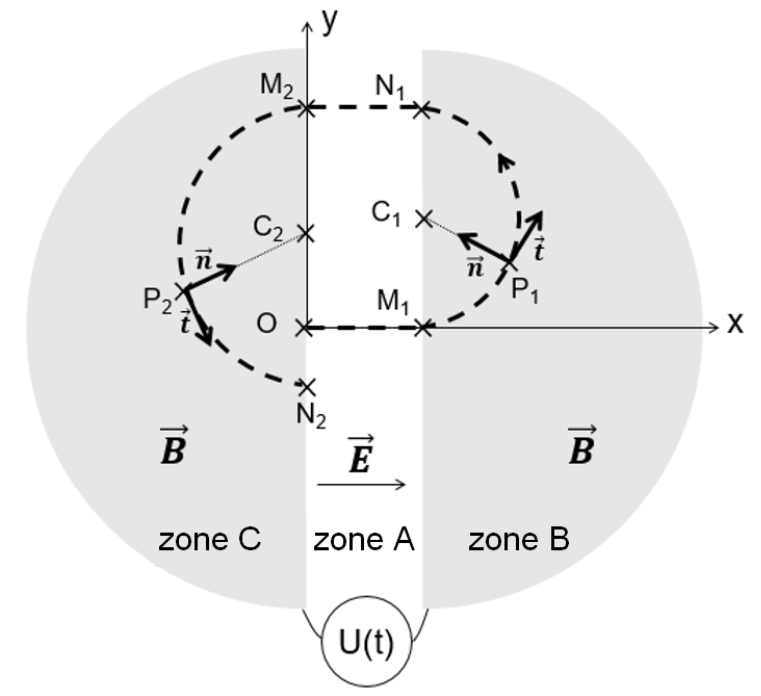
Figure 4. Trajectoire du proton pour un tour dans le cyclotron.

La figure 5 représente la valeur de la vitesse du proton en fonction du temps, lorsqu’il parcourt un tour dans le cyclotron : du point O, au point N₂.

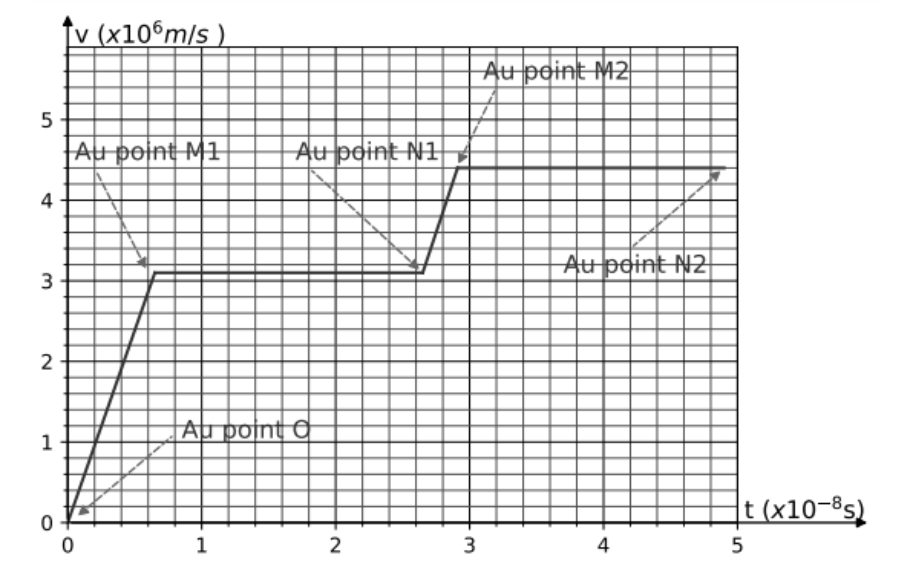
Figure 5. Valeur de la vitesse v du proton en fonction du temps.

Données :

• Les repères d’étude sont : le repère orthonormé (O,x,y) pour la zone A et le repère local de Frenet $(P,\overrightarrow{t},\overrightarrow{n})$ pour les zones B et C avec P le centre du proton ;
• Zone C : Rayon de la trajectoire circulaire: R₂ = C₂P₂ = 3,9 cm.

Q7. Déterminer à l’aide des figures 4 et 5 la valeur du vecteur accélération :

• Entre les points N₁ et M₂ : retour dans la zone A, la valeur du vecteur accélération sera notée a_A ;
• Entre les points M₂ et N₂ : passage dans la zone C, la valeur du vecteur accélération sera notée a_C.

$$a=\frac{dv}{dt}$$

Entre les points N1 et M2 : retour dans la zone A, la valeur du vecteur accélération sera notée aA ;
$$a_A=\frac{\Delta v}{\Delta t}$$
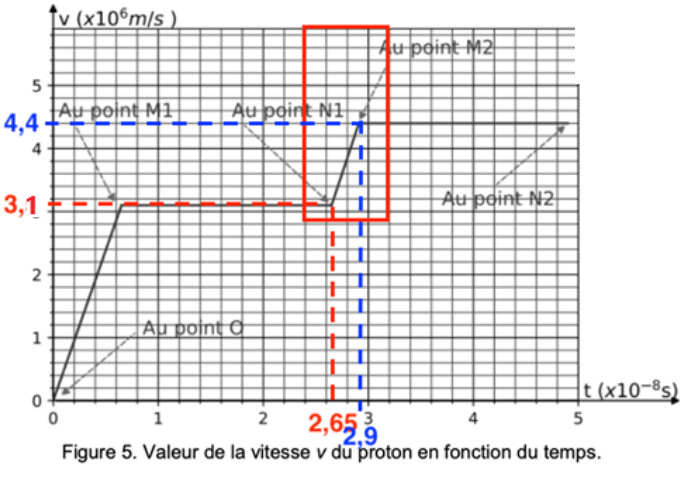
$$a_A=\frac{v_{M_2}-v_{N_1}}{t_{M_2}-t_{N_1}}$$
$$a_A=\frac{4,4\times {10}^6-3,1\times {10}^6}{2,9\times {10}^{-8}-2,65\times {10}^{-8}}$$
$$a_A=5,2\times {10}^{14}\ m.s^{-2}$$

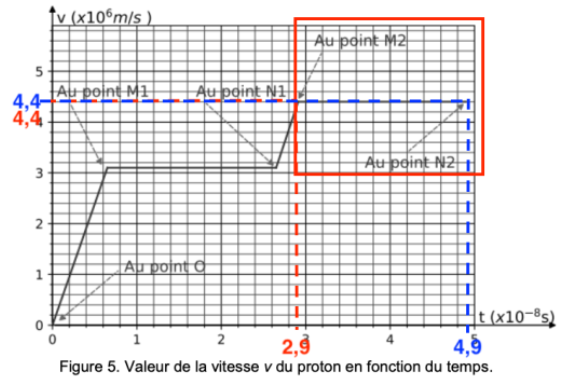
Entre les points M2 et N2 : passage dans la zone C, la valeur du vecteur accélération sera notée aC.
La vitesse est constante : $v_{N_2}=v_{M_2}=4,4\times {10}^6\ m.s^{-1}$. Le mouvement est uniforme.

De plus, le mouvement est circulaire.

Pour un mouvement circulaire uniforme, l’accélération est de la forme :
$$a_C=\frac{v^2}{R_2}$$
$$a_C=\frac{\left(4,4\times {10}^6\right)^2}{3,9\times {10}^{-2}}$$
$$a_C=5,0\times {10}^{14}\ m.s^{-2}$$