E3C2 – 10 points – Durée 1h – calculatrice autorisée
Sujet n°G1SPHCH02715 ,n°G1SPHCH02774 et n°G1SPHCH02694
Télécharger l’exercice en PDF :
Le jet d’eau de Genève, en Suisse, est l’emblème de la ville. Il permettait à l’origine de contrôler la pression d’une usine hydraulique en laissant s’échapper vers le ciel l’eau en surpression.

(d’après wikipedia.org/Jet_d’eau.jpg)
Le but de cet exercice est de discuter de deux différentes modélisations permettant d’étudier le mouvement du jet d’eau.
Données techniques :
- hauteur moyenne du jet : 140 m ;
- vitesse de sortie de l’eau : 200 km.h-1 ;
- débit : 500 L.s-1 ;
- puissance des pompes : 1000 kW ;
- intensité du champ de pesanteur terrestre :
g = 9,81 m.s-2.
1. Estimation de la hauteur du jet
On souhaite estimer la hauteur du jet à l’aide d’un modèle très simple. On s’intéresse à une goutte d’eau de masse m initialement au niveau du sol, à qui on communique une vitesse v0=56m.s-1,soit 200 km.h-1, dirigée verticalement vers le haut.
Dans cette partie, on néglige les frottements de l’air sur la goutte. La hauteur du jet est notée h1. L’origine des altitudes pour le calcul de l’énergie potentielle de pesanteur est choisie à la surface du lac, où est située la sortie des pompes et l’axe Oz est orienté vers le haut.
1.1. Donner l’expression de l’énergie mécanique de la goutte en fonction de sa masse m, de sa vitesse v, de son altitude z et du champ de pesanteur terrestre g.
$$E_M = E_c + E_p$$
$$E_M = \frac{1}{2} m v^2 + m g z$$
1.2. En déduire l’expression de l’énergie mécanique en sortie des pompes en fonction de v0 et m.
$$E_{M(0)} = \frac{1}{2} m v_0^2 + m g z_0$$
$$E_{M(0)} = \frac{1}{2} m v_0^2$$
1.3. Indiquer en justifiant la valeur de l’énergie cinétique de la goutte en haut du jet. En déduire l’expression de l’énergie mécanique en haut du jet en fonction de la hauteur h1 du jet, de g et de m.
L’énergie cinétique de la goutte en haut du jet est nulle car elle ne monte plus, la goutte n’a plus de vitesse.
$$E_{M(1)} = \frac{1}{2} m v_1^2 + m g z_1$$
$$E_{M(1)} = m g z_1$$
$$E_{M(1)} = m g h_1$$
1.4. Dans cette partie, on considère que l’énergie mécanique de la goutte se conserve. Estimer la hauteur h1 du jet. Commenter votre résultat.
L’énergie mécanique de la goutte se conserve : $E_{M(1)} = E_{M(0)}$
$$m g h_1 = \frac{1}{2} m v_0^2$$
$$g h_1 = \frac{1}{2} v_0^2$$
$$h_1 = \frac{v_0^2}{2 g}$$
$$h_1 = \frac{\left(\frac{200}{3,6}\right)^2}{2 \times 9,81} = 157 m$$
D’après les données techniques la hauteur moyenne du jet : 140 m.
La différence entre la valeur trouvée et la valeur réelle est due au fait que l’énergie ne se conserve pas, il faut prendre en compte les forces de frottements.
2. Un modèle plus complexe
Une modélisation plus complexe permet d’obtenir les expressions de l’altitude z et de la vitesse v de la goutte en fonction du temps. On utilise le langage python afin d’obtenir le graphique des différentes énergies en fonction du temps.
Dans cette partie, la hauteur du jet est notée h2.
Extrait du programme réalisé en python :

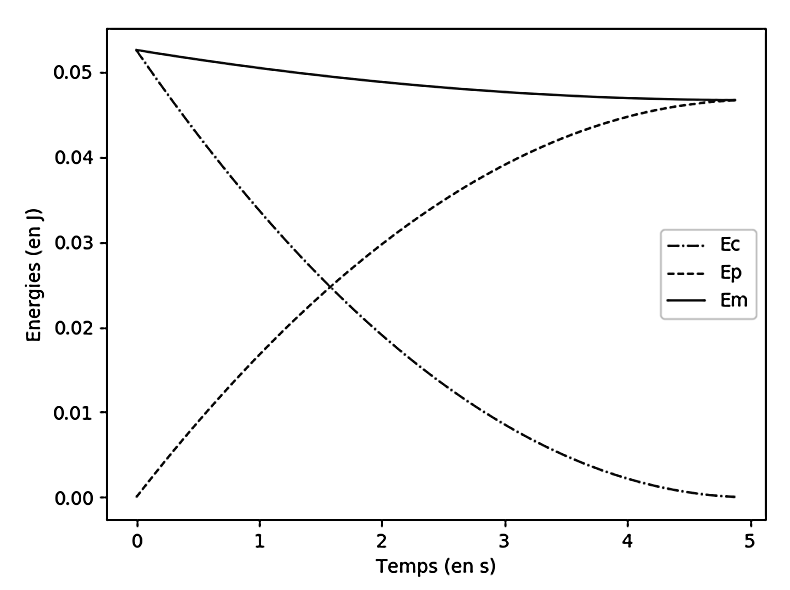
2.1. Compléter les lignes 26 et 27 du programme en python afin qu’il permette d’obtenir la représentation graphique de la figure 2.
Nous souhaitons obtenir les graphiques Ec et Ep. Ainsi il faut écrire leurs formules. Remarques :
- le fois en python se note *
- La puissance en python se note **
26 Ec=0,5*m*v**2
27 Ep=m*g*z
2.2. Commenter l’évolution de l’énergie mécanique de la goutte obtenue sur le graphique (figure 2). Indiquer en quoi la modélisation choisie ici permet d’obtenir des résultats plus en accord avec la réalité que le modèle proposé dans la partie 1.
La courbe de l’énergie mécanique décroit. Ainsi l’énergie mécanique ne se conserve pas.
La modélisation choisie ici permet d’obtenir des résultats plus en accord avec la réalité que le modèle proposé dans la partie 1 car elle prend en compte que l’énergie mécanique ne se conserve pas à cause des frottements.
2.3. La norme de la force de frottement, supposée constante, qui s’applique sur la goutte est notée f.
2.3.1. Relier la variation d’énergie mécanique de la goutte entre sa position haute et sa position basse ΔEm à la hauteur du jet h2et à la norme force de frottement f. En déduire l’expression de f.
Théorème de l’énergie mécanique
$$\Delta E_m = \Sigma W(\overrightarrow{F}_{non\ conservatives})$$
$$\Delta E_m = W(\overrightarrow{f})$$
$$\Delta E_m = – f \times h_2$$
$$f = \frac{- \Delta E_m}{h_2}$$
2.3.2. La valeur choisie dans le programme pour f permet d’obtenir une valeur de 140 m pour la hauteur h2 du jet. À l’aide du graphique figure 2, évaluer ΔEm. En déduire la valeur choisie pour la norme de la force de frottement.
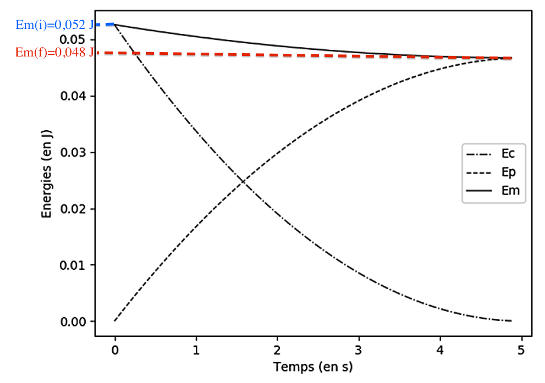
$$f = \frac{- \Delta E_m}{h_2} = \frac{-(0,048 – 0,052)}{140} = 2,85.10^{-5} N$$
2.3.3. Les équations de la mécanique des fluides permettent d’établir que la force de frottement est proportionnelle au carré de la vitesse de la goutte. Indiquer une éventuelle amélioration à apporter à la modélisation utilisée dans la partie 2. Expliquer votre choix.
Nous allons modifier le programme en prenant en compte que la force de frottement est proportionnelle au carré de la vitesse
19 : au lieu de f = 1,24*m, mettre f = k*v0**2 (avec une valeur pour k)
