Bac Métropole Mars 2021 Sujet 1
Exercice 1 – (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
EXERCICE 1 commun à tous les candidats (10 points) LE JEU DU CORNHOLE
Le Cornhole, contraction des mots anglais « corn » et « hole » voulant dire « maïs » et « trou », est un jeu de plein air pratiqué entre autres aux États-Unis et au Canada.
Les règles de ce jeu sont assez simples. Chaque joueur est muni de quatre petits sacs contenant du maïs qu’il doit lancer en direction d’une planche inclinée par rapport à l’horizontale munie d’un trou circulaire et située environ à 8 mètres du joueur. À chaque fois qu’un sac retombe sur la planche, le joueur marque un point ; si le sac passe par le trou circulaire, le joueur marque trois points. Le premier joueur qui marque 21 points gagne la partie.

Extrait du site Internet www.quora.com
On étudie dans cet exercice les aspects énergétiques du lancer du sac puis le mouvement du centre de masse du sac dans le référentiel terrestre supposé galiléen.
Données :
- intensité de la pesanteur terrestre : g = 9,81 m·s-2 ;
- masse du sac : m = 440 g.
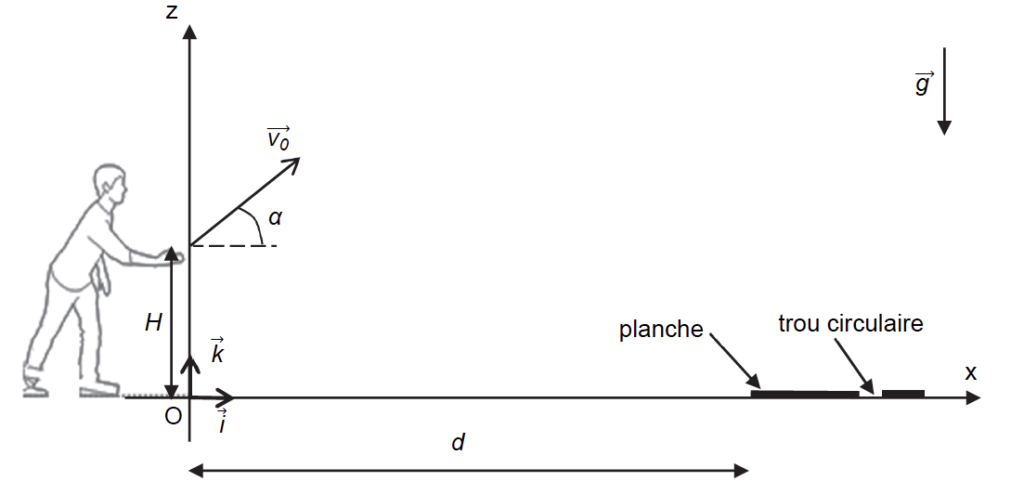
Un joueur se place à une distance d de la planche afin de réaliser un lancer de son sac de maïs. La situation est représentée sur la figure 1 ci-dessous. Afin de simplifier l’étude, la planche est considérée quasi-
horizontale. Dans le repère d’espace (Ox, Oz) muni des vecteurs unitaires ![]() et
et ![]() , le sac de maïs est lancé, depuis une hauteur initiale H, avec une vitesse initiale dont le vecteur
, le sac de maïs est lancé, depuis une hauteur initiale H, avec une vitesse initiale dont le vecteur ![]() est incliné d’un angle α par rapport à l’horizontale. On s’intéresse au mouvement du centre de masse G du sac. L’axe (Oz) du repère d’espace est vertical.
est incliné d’un angle α par rapport à l’horizontale. On s’intéresse au mouvement du centre de masse G du sac. L’axe (Oz) du repère d’espace est vertical.
1. Étude énergétique
Le mouvement complet du sac est filmé puis étudié à l’aide d’un logiciel de pointage. Les données de la partie ascendante du mouvement sont traitées à l’aide d’un programme écrit en langage python (extrait en figure 2) qui permet de représenter l’évolution au cours du temps des énergies cinétique (Ec), potentielle de pesanteur (Epp) et mécanique (Em) du sac (figure 3).
| 1 | #importation des bibliothèques utilisées |
| 2 | import numpy as np |
| 3 | import matplotlib.pyplot as plt |
| 4 | |
| 5 | # valeurs experimentales |
| 6 | z=np.array([0.869,0.996,1.17,1.3,1.41,1.51,1.6,1.67,1.75,1.82,1.86,1.92,1.94,1.94,1.97,1.96,1.96]) |
| 7 | t=np.array([0,0.033,0.067,0.1,0.133,0.167,0.2,0.233,0.267,0.3,0.333,0.367,0.4,0.433,0.467,0.5,0.533]) |
| 8 | vx=np.array([7.61,7.66,7.712,7.517,7.595,7.578,7.334,7.39,7.329,7.184,7.239,7.116,7.065,7.119,6.997,7.006,6.997]) |
| 9 | vz=np.array([4.8,4.484,4.158,3.797,3.219,2.787,2.515,2.314,2.008,1.827,1.447,0.9539,0.7198,0.3329,0.1782, |
| 10 | -0.02958,-0.4165]) |
| 11 | |
| 12 | #Calcul des énergies |
| 13 | m=0.440 |
| 14 | g=9.81 |
| 15 | ? = (vx**2 + vz**2)**(1/2) |
| 16 | ? = 0.5*m*v**2 |
| 17 | ? = m*g*z |
| 18 | ? = 0.5*m*v**2 + m*g*z |
| 19 |
Figure 2. Extrait du programme écrit en langage python
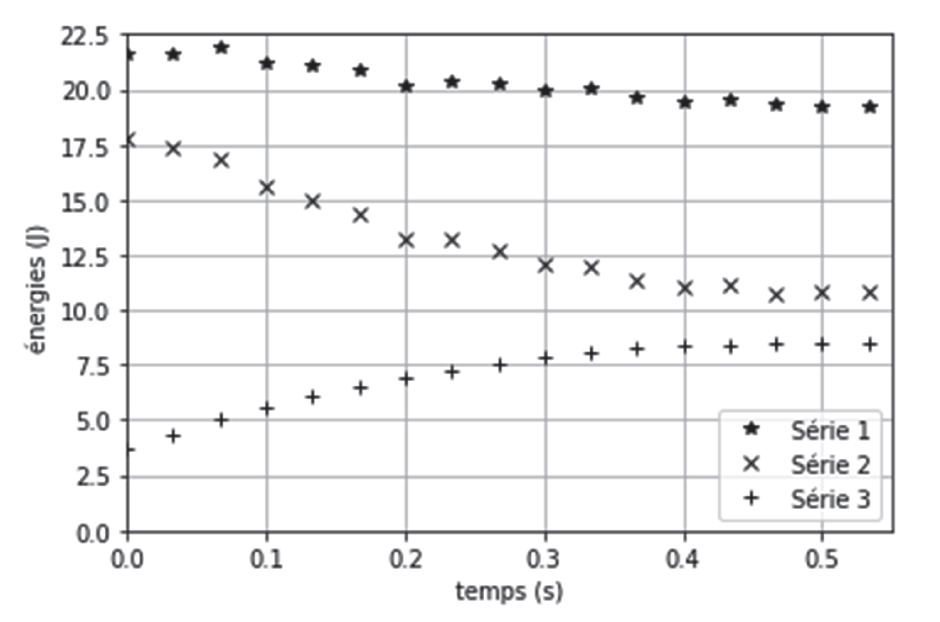
Figure 3. Évolution des énergies cinétique, potentielle de pesanteur et mécanique du sac au cours du temps obtenue à l’aide du programme écrit en langage python
1.1. Identifier les grandeurs calculées dans l’extrait du programme écrit en langage python (figure 2) aux lignes 15, 16, 17 et 18.
1.2. Exploitation de la figure 3
1.2.1. En justifiant votre choix, attribuer à chaque série l’énergie qui lui correspond.
1.2.2. Expliquer en quoi les résultats expérimentaux permettent de considérer que l’action de l’air sur le sac n’est pas négligeable devant le poids du sac.
1.2.3. Estimer la valeur de la vitesse initiale v0 du centre de masse du sac.
1.2.4. Estimer la valeur de l’altitude initiale H du centre de masse du sac. Commenter.
2. Étude du mouvement du sac après le lancer
On souhaite étudier la chute du sac au cours du temps. La situation est toujours représentée sur la figure 1. Les frottements ne seront pas pris en compte dans cette partie.
On souhaite établir les expressions littérales des grandeurs accélération, vitesse et position du sac lors de son mouvement, ainsi que les caractéristiques (vitesse initiale et direction initiale) nécessaires à la réussite d’un lancer valant trois points.
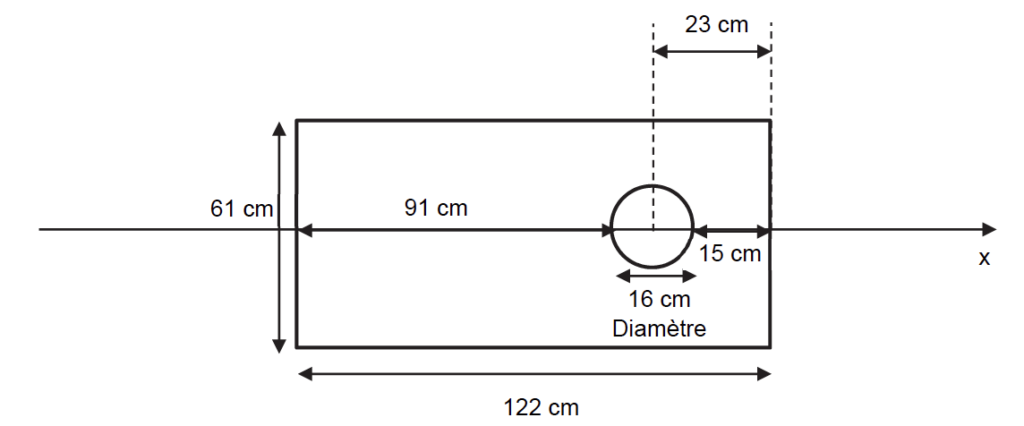
Les dimensions de la planche sont précisées sur la figure 4 ci-dessous :
2.1. Déterminer les expressions littérales des coordonnées ax et az du vecteur accélération ![]() du centre de masse du sac suivant les axes Ox et Oz.
du centre de masse du sac suivant les axes Ox et Oz.
Réponse :
Système {sac}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
![]()
![]()
![]()
![]()
Or
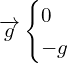
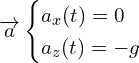
2.2. En déduire les expressions littérales des équations horaires x(t) et z(t) de la position du centre de masse du sac au cours du mouvement.
Réponse :
![]()
On intègre le système d’équation précédent :
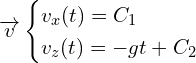
Pour trouver les constantes, on utilise ![]() :
:
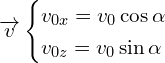
d’ou
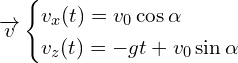
![]()
On intègre le système d’équation précédent :
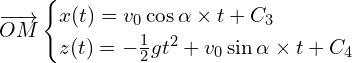
Pour trouver les constantes, on utilise ![]()
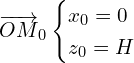
d’ou
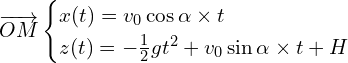
2.3. Montrer que l’équation littérale de la trajectoire du centre de masse du sac dans le repère d’espace (Ox, Oz) est :
![]()
Qualifier cette trajectoire.
2.4. Indiquer les paramètres initiaux de lancement sur lesquels le joueur peut avoir une influence et qui jouent un rôle pour la réussite d’un lancer à trois points.
Le joueur effectue un premier lancer. L’équation de la trajectoire du centre de masse du sac a pour expression numérique :
z(x) = – 0,0842 x2 + 0,625 x + 0,880 avec x et z en m
La distance d qui sépare l’origine O du repère d’espace et le bord de la planche est égale à d = 8,0 m.
2.5. Déterminer le nombre de point(s) marqué(s) par le joueur pour ce lancer.
2.6. Le joueur effectue un second lancer en conservant le même angle de tir α, la même hauteur initiale H mais en modifiant la valeur de la vitesse initiale par rapport au premier lancer.
Déterminer une valeur possible de la nouvelle vitesse initiale v0 , afin que le sac tombe directement dans le trou. Commenter la valeur obtenue.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
