Bac Amérique du nord 2021 Sujet 1
Exercice 1– (10 points) – Commun à tous les candidats – Durée 1h45 – Calculatrice autorisée
Sujet n° 21-PYCJ1AN1
Le lancer de gerbe de paille est une activité sportive, issue du domaine agricole, qui se pratique aujourd’hui en compétition. Le but du jeu est de lancer, à l’aide d’une fourche, une gerbe de paille, assimilable à un parallélépipède rectangle de longueur 0,60 m, de largeur 0,40 m et d’épaisseur 0,40 m, au-dessus d’une barre horizontale placée à une hauteur bien précise.

A. Étude du lancer
On modélise la situation en compétition de la manière suivante :
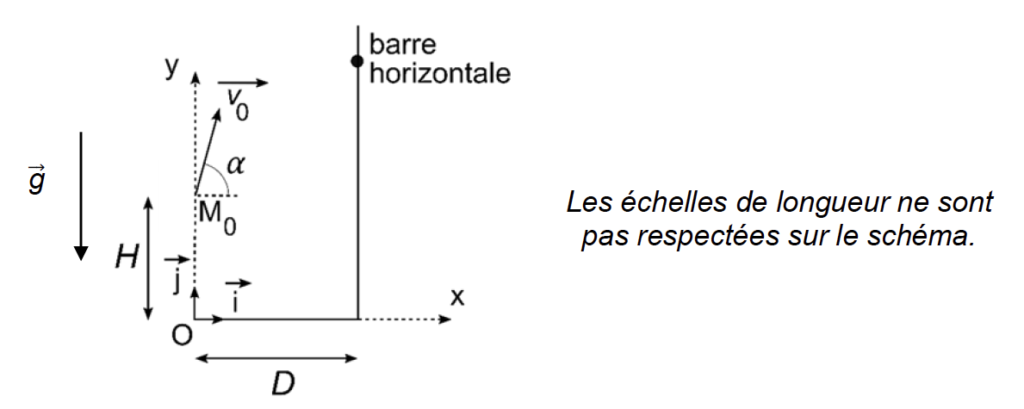
- La gerbe de paille de masse m = 7,257 kg est assimilée à un point matériel M, correspondant au centre masse.
- À l’instant initial, M se trouve au point M0 tel que OM0 = H = 2,80 m.
- Le lanceur se trouve à la distance D = 2,0 m de la base des supports de la barre horizontale.
- L’étude débute à t = 0 quand la gerbe de paille vient de quitter la fourche (au point M0) avec une vitesse initiale représentée par le vecteur vitesse
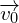 incliné d’un angle α = 80° par rapport à l’horizontale. La valeur de la vitesse initiale est v0 = 9,0 m·s-1.
incliné d’un angle α = 80° par rapport à l’horizontale. La valeur de la vitesse initiale est v0 = 9,0 m·s-1. - On suppose que la trajectoire de M s’effectue dans le plan xOy.
- La barre horizontale est à une hauteur de 4,50 m par rapport au sol.
- L’action de l’air est négligée.
- Le champ de pesanteur, considéré comme uniforme, vaut g = 9,8 m·s-2.
On étudie le mouvement de M dans le référentiel terrestre dont le repère xOy est défini sur le schéma introductif.
A.1. Utiliser la deuxième loi de Newton pour déterminer les coordonnées ax(t) et ay(t) du vecteur accélération de M.
Réponse :
Système {gerbe de paille}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
![]()
![]()
![]()
![]()
Or
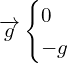
Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
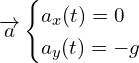
A.2. Montrer que les équations horaires du mouvement de M s’expriment sous la forme :
![]()
![]()
Réponse :
![]()
On intègre le système d’équation précédent :
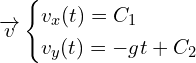
Pour trouver les constantes, on utilise ![]() :
:
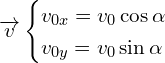
d’ou
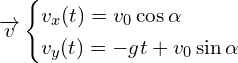
![]()
On intègre le système d’équation précédent :
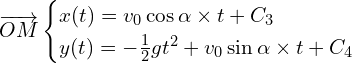
Pour trouver les constantes, on utilise ![]()
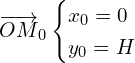
d’ou
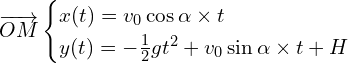
A.3. En déduire l’équation de la trajectoire y(x) de M.
Réponse :
![]()
![]()
On remplace t dans y :
![]()
![]()
![]()
A.4. À l’aide d’une analyse quantitative, indiquer si la gerbe de paille franchira, ou pas, la barre horizontale.
Réponse :
La barre horizontale se situe à x=D.
Trouvons y pour x=D :
![]()
![]()
![]()
La barre est située à une hauteur de 4,5 m. La gerbe franchira donc la barre.
On s’intéresse à trois positions particulières de M sur sa trajectoire parabolique : la position initiale M0, le point M1 au sommet de la trajectoire et le point M2 à la même hauteur que M0 par lequel passe M lors de la phase descendante du mouvement.
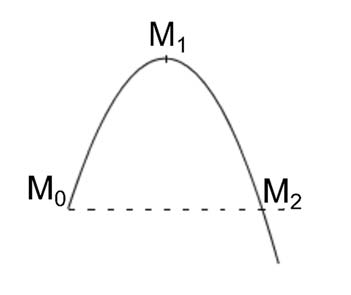
L’énergie potentielle de pesanteur est choisie nulle au niveau du sol.
A.5. Calculer la valeur de l’énergie cinétique et celle de l’énergie potentielle de pesanteur du système en M0.
Réponse :
Energie cinétique : ![]()
![]()
![]()
![]()
Energie potentielle : ![]()
![]()
![]()
![]()
![]()
A.6. Indiquer par un raisonnement détaillé si chacune des trois propositions suivantes est vraie, ou fausse, lorsque l’on néglige l’action de l’air.
Proposition I : l’énergie mécanique est maximale en M0.
Proposition II : l’énergie cinétique est nulle en M1.
Proposition III : l’énergie cinétique en M2 est inférieure à l’énergie cinétique en M0.
Réponse :
Proposition 1 : Lorsqu’on néglige l’action de l’air, l’énergie mécanique se conserve. Ainsi, elle est constante sur tout le trajet. Elle est donc maximale en M0. Donc la proposition 1 est vraie.
Proposition 2 : au point M1, la gerbe ne monte plus, sa vitesse verticale est nulle vy=0. Cependant sa vitesse horizontale v(x(t))=v0 cos α n’est pas nulle. vx est constante sur toute la trajectoire. Donc la proposition 2 est fausse.
Proposition 3 : Lorsqu’on néglige l’action de l’air, l’énergie mécanique se conserve. Ainsi, elle est constante sur tout le trajet.
EM0=EM2
Ec0+Epp0=Ec2+Epp2
Or Epp0=Epp2 car ils sont à la même altitude.
Donc : Ec0=Ec2
L’énergie cinétique en M2 est égale à celle en M0. Donc la proposition 3 est fausse.
En réalité, l’action de l’air ne peut pas être négligée.
A.7. Indiquer par un raisonnement détaillé si chacune des trois propositions de la question A.6. reste vraie, ou fausse, lorsqu’on ne néglige plus l’action de l’air.
Réponse :
Proposition 1 : Lorsqu’on ne néglige plus l’action de l’air, l’énergie mécanique ne se conserve pas. Ainsi, elle décroit sur tout le trajet. Elle est donc maximale en M0. Donc la proposition 1 est vraie.
Proposition 2 : au point M1, la gerbe ne monte plus, sa vitesse verticale est nulle vy=0. Cependant sa vitesse horizontale v(x(t))=v0 cos α n’est pas nulle. vx est constante sur toute la trajectoire. Donc la proposition 2 est fausse.
Proposition 3 : Lorsqu’on ne néglige plus l’action de l’air, l’énergie mécanique ne se conserve pas. Ainsi, elle décroit sur tout le trajet.
EM0>EM2
Ec0+Epp0>Ec2+Epp2
Or Epp0=Epp2 car ils sont à la même altitude.
Donc : Ec0=Ec2
Donc : Ec0>Ec2 L’énergie cinétique en M2 est supérieure à celle en M0. Donc la proposition 3 est vraie.
B. Le microphone de l’animateur
L’animateur de la compétition du lancer de gerbe de paille utilise un microphone relié à une enceinte acoustique par l’intermédiaire d’un amplificateur de puissance.
Le microphone utilisé lors de la compétition est un transducteur électroacoustique. Il permet de convertir un signal acoustique en un signal électrique.
Schéma de principe du microphone
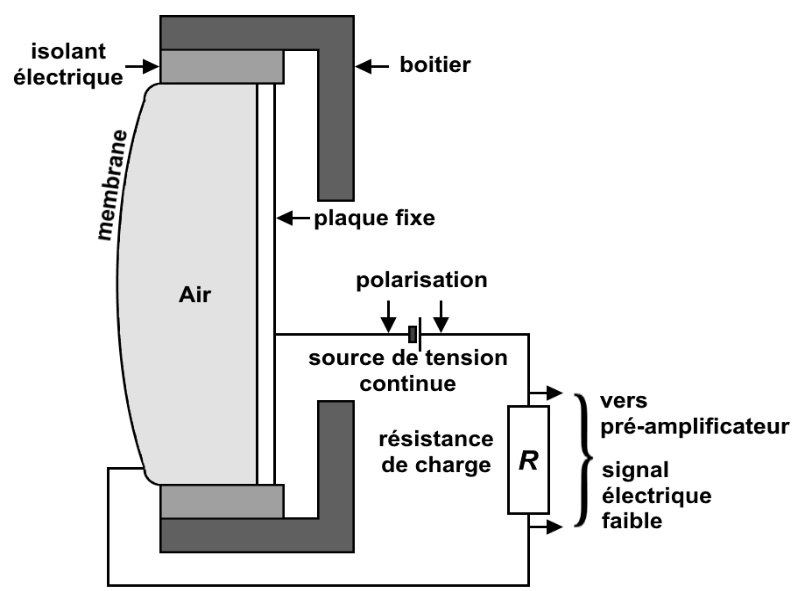
Le condensateur présent dans le microphone est formé de deux armatures ; la première est constituée d’une membrane mobile en plastique recouverte d’une fine pellicule métallique, la seconde est constituée d’une plaque métallique fixe. Lorsque le microphone ne capte pas de son, la distance entre les deux armatures est de l’ordre de 15 à 25 µm.
En outre, pour fonctionner, le condensateur doit être chargé ; on insère donc une source de tension continue qui n’a pas d’effet sur le signal électrique de sortie envoyé vers le pré-amplificateur.
On modélise alors le microphone par le circuit électrique suivant :
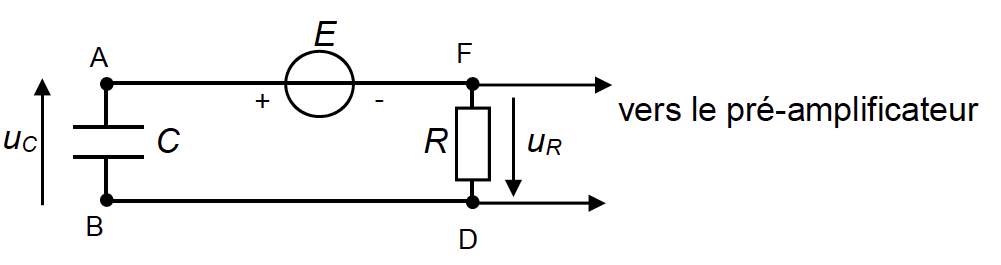
Tension continue délivrée par la source idéale : E = 48 V
Résistance du conducteur ohmique de charge : R = 100 × 106 Ω
Capacité du condensateur : C
Pour fonctionner, le condensateur doit rester chargé. On étudie la phase de charge, le microphone ne captant pas de son.
B.1. Établir la relation entre la tension E aux bornes de la source de tension idéale, la tension uc(t) aux bornes du condensateur et la tension uR(t) aux bornes du conducteur ohmique.
Réponse :
D’après la loi d’additivité des tensions ou loi des mailles :
![]()
B.2. Montrer que l’équation différentielle vérifiée par la tension uc(t) lors de la charge est de la forme :
![]()
Réponse :
![]()
Or ![]()
![]()
Or ![]()
![]()
Or ![]()
![]()
![]()
![]()
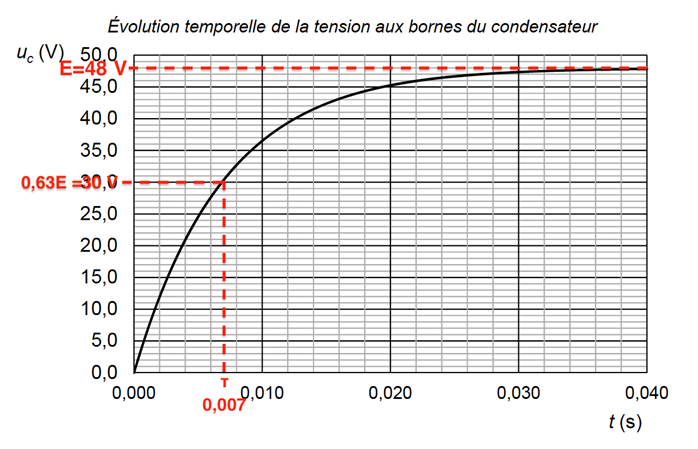
Grâce à un dispositif approprié, on mesure la tension uc(t) aux bornes du condensateur lors de sa charge. On obtient la courbe suivante.
Évolution temporelle de la tension aux bornes du condensateur
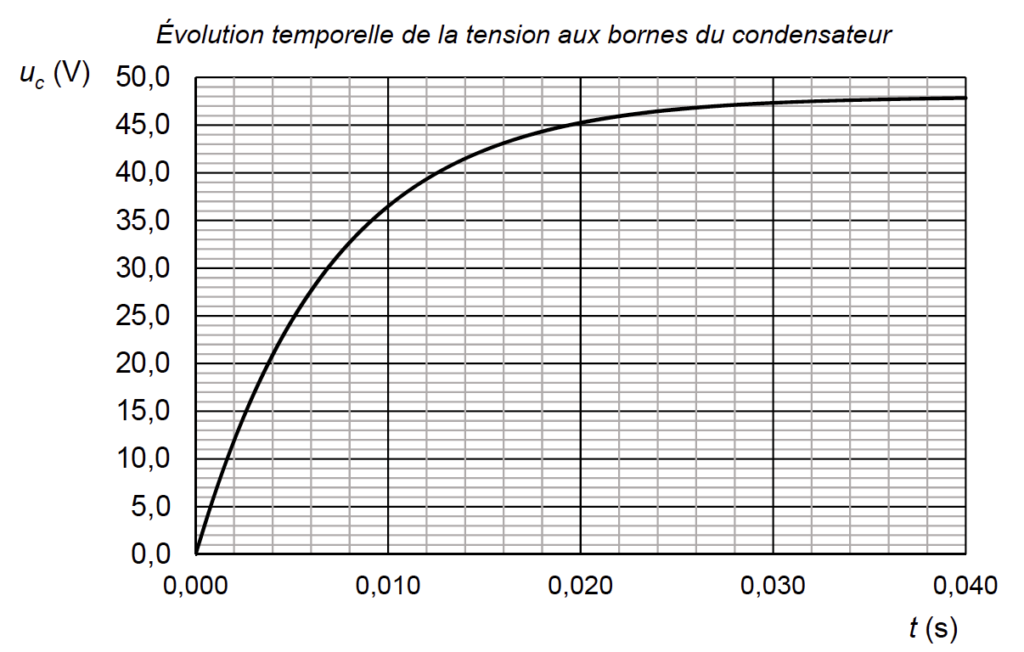
Cette courbe peut être modélisée par une des trois fonctions mathématiques proposées ci-dessous :
Fonction 1 : ![]() Fonction 2 :
Fonction 2 : ![]()
Fonction 3 : ![]()
B.3. En exploitant la courbe, indiquer par un raisonnement argumenté la fonction qui modélise la charge du condensateur.
Réponse :
Graphiquement UC (t=0)=0 V
Pour chaque fonction proposée calculons UC (t=0)
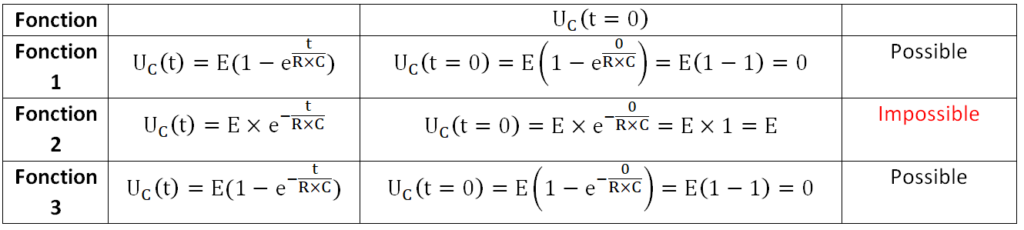
Graphiquement UC (t→∞)=E
Pour chaque fonction proposée calculons UC (t→∞)
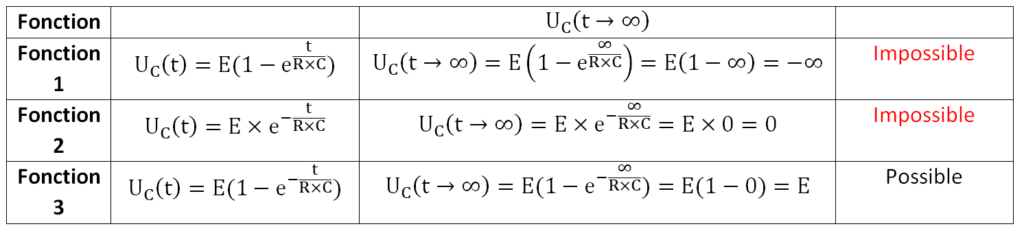
La seule proposition qui convient pour ces deux conditions est la fonction 3 : ![]()
B.4. Vérifier que la fonction retenue est solution de l’équation différentielle établie à la question B.2.
Réponse :
Vérifions que la fonction retenue est solution de l’équation différentielle :
![]()
-Dérivons UC (t) :
![]()
![]()
-Remplaçons ![]() et
et ![]() dans l’équation :
dans l’équation :
![]()
![]()
![]()
![]()
La fonction retenue est bien solution de l’équation différentielle.
La capacité C d’un condensateur plan constitué de deux armatures métalliques de surface S en regard l’une de l’autre, séparées d’une distance d, est donnée par la relation ![]() avec ε la permittivité de l’air entre les deux armatures du condensateur. Pour le microphone étudié, le produit de la permittivité de l’air par la surface est : ε·S = 1,4 × 10-15 F·m.
avec ε la permittivité de l’air entre les deux armatures du condensateur. Pour le microphone étudié, le produit de la permittivité de l’air par la surface est : ε·S = 1,4 × 10-15 F·m.
B.5. En exploitant la courbe et en explicitant le raisonnement, déterminer la valeur de la distance d séparant les deux armatures quand le microphone fonctionne mais qu’il ne capte pas de son.
Réponse :
![]()
![]()
Or ![]()
![]()
D’ou
![]()
![]()
A l’aide de la courbe, trouvons τ : τ=0,007 s
![]()
![]()
![]()
Remarque : la distance trouvée correspond à la distance attendue » la distance entre les deux armatures est de l’ordre de 15 à 25 μm »
Sous l’effet des ondes sonores émises par l’animateur, la membrane se déplace en entraînant une modification de la distance entre les deux armatures du condensateur. La tension de sortie envoyée vers le pré-amplificateur est alors l’image des ondes sonores captées par le microphone.
B.6. Justifier par un raisonnement détaillé l’évolution de la capacité du condensateur lorsque la distance séparant les deux armatures diminue.
Réponse :
![]()
C est inversement proportionnel à d. Ainsi, quand d diminue, C augmente.
C. L’enceinte
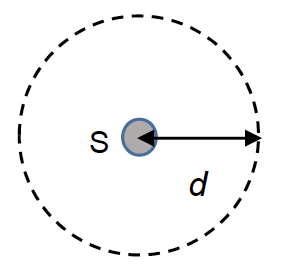
Une source S, émettant des ondes sonores de puissance P, est isotrope si elle émet la même quantité d’énergie dans toutes les directions. L’intensité sonore mesurée, notée I, dépend alors de la distance d à la source selon la relation : ![]() avec I en W·m-2 ; P en W et d en m.
avec I en W·m-2 ; P en W et d en m.
Le niveau d’intensité sonore, noté L, est lié à l’intensité sonore par la relation :
![]() avec L exprimé en dB, I en W·m-2 et I0 = 1,0 × 10-12 W·m-2.
avec L exprimé en dB, I en W·m-2 et I0 = 1,0 × 10-12 W·m-2.
Le microphone est relié, par l’intermédiaire d’un amplificateur de puissance, à une enceinte. L’intensité sonore mesurée à 1,0 m devant l’enceinte vaut : I1 = 3,2 × 10-3 W·m-2.
C.1. Calculer le niveau d’intensité sonore L1 correspondant à l’intensité sonore I1.
Réponse :
![]()
![]()
![]()
La législation européenne indique les durées limites d’exposition journalière à ne pas dépasser à certains niveaux d’intensité sonore pour ne pas engendrer des traumatismes irréversibles :
| L (dB) | 86 | 92 | 95 | 101 | 107 |
| Durée limite d’exposition | 2 h/jour | 30 min/jour | 15 min/jour | 4 min/jour | 1 min/jour |
C.2. Commenter le résultat de la question C.1. au regard de ces durées limites d’exposition journalière.
Réponse :
Pour un niveau d’intensité sonore de 95 dB, la durée maximale d’exposition est de 15 min/jour pour ne pas engendrer des traumatismes irréversibles.

Ainsi, ce niveau est très élevé.
C.3. Montrer que la puissance P de l’enceinte est égale à 4,0 × 10-2 W.
Réponse :
![]()
![]()
![]()
![]()
Les organisateurs de la manifestation sportive, d’une durée de 2 h, ont fixé à 2,0 × 10-4 W·m-2 la valeur maximale de l’intensité sonore perçue par les spectateurs.
C.4. Expliquer le choix des organisateurs de fixer à 2,0 × 10-4 W·m-2 la valeur maximale de l’intensité sonore perçue par les spectateurs.
Réponse :
Calculons le un niveau d’intensité sonore pour I=2,0 × 10-4 W·m-2
![]()
![]()
![]()
La manifestation sportive doit durée 2h. Afin de respecter la réglementation, les organisateurs doivent émettre au maximum 86 dB.
Par mesure de sécurité, ils choisissent un niveau maximum inferieur à cette limite :
L= 83 dB pour I=2,0 × 10-4 W·m-2
Des barrières de sécurité entourent l’enceinte à 3,0 m de celle-ci, pour éviter que les spectateurs en soient trop proches.
C.5. Indiquer, par un raisonnement quantitatif, si la distance de sécurité entre les barrières et l’enceinte est suffisante pour respecter la valeur maximale de 2,0 × 10-4 W·m-2 choisie par les organisateurs.
Réponse :
Calculons la distance de sécurité minimale pour respecter la valeur I=2,0 × 10-4 W·m-2
![]()
![]()
![]()
![]()
![]()
En plaçant la barrière à 3,0 m, la distance n’est pas suffisante pour respecter la valeur I=2,0 × 10-4 W·m-2
