Le paradoxe du Soleil pâle

Sujet sans enseignement de mathématiques spécifique

Enseignement scientifique première

Durée 1h – 10 points – Thème « Le Soleil, notre source d’énergie »

Le système solaire s’est formé il y a 4,57 milliards d’années. Le paradoxe du jeune Soleil pâle désigne la contradiction apparente, entre la présence d’eau liquide sur Terre à cette époque et le fait que le Soleil ne brillait qu’à 70 % de son intensité actuelle. La température sur Terre devait être inférieure à 0 °C et donc l’eau aurait dû être présente à l’état solide uniquement.

L’objectif de cet exercice est d’étudier ce paradoxe.

Partie 1 – Caractérisation du Soleil jeune

Actuellement, la puissance surfacique moyenne du rayonnement solaire arrivant à la surface de l’atmosphère terrestre est de 340 W · m⁻².

1 – Montrer que la puissance surfacique moyenne solaire qui atteignait la surface de l’atmosphère terrestre il y a 4 milliards d’années était d’environ 240 W · m⁻².

Le Soleil ne brillait qu’à 70 % de son intensité actuelle. Actuellement, la puissance surfacique moyenne du rayonnement solaire arrivant à la surface de l’atmosphère terrestre est de 340 W · m⁻².

$P_{S,\ 4m}=\frac{70}{100} \times P_{S,\ actu}$

$P_{S,\ 4m}=\frac{70}{100} \times 340 P_{S,\ 4m}=238\ W.m^{-2}$

Ainsi, la puissance surfacique moyenne solaire qui atteignait la surface de l’atmosphère terrestre il y a 4 milliards d’années était d’environ 240 W · m⁻².

Document 1 – Loi de Stefan

La puissance émise par unité de surface (𝑃 exprimée en W · m⁻²) est proportionnelle à la puissance quatrième de la température (𝑇 exprimée en Kelvin).

𝑃 = 𝜎 × 𝑇⁴

avec 𝜎, constante de Stefan-Boltzmann valant 5,67 × 10⁻⁸ W · m⁻² · K⁻⁴.

Relation entre la température 𝜽(°𝐂) et la température 𝑻(𝐊) :

𝑇 = 𝜃 + 273

2 – À l’aide du document 1, montrer qu’en première approximation, la température de la Terre aurait dû être d’environ −18°C il y a 4 milliards d’années.

$P=\sigma \times T^4$

$\sigma \times T^4=P$

$T^4=\frac{P}{\sigma}$

$T=\sqrt[4]{\frac{P}{\sigma}}$

$T=\sqrt[4]{\frac{240}{5,67 \times {10}^{-8}}}$

T=255 K

T=𝜃 +273

𝜃+273=T

𝜃=T-273

𝜃=255-273

𝜃 =-18 °C

Ainsi, en première approximation, la température de la Terre aurait dû être d’environ −18°C il y a 4 milliards d’années.

Document 2 – Lien entre luminosité et température de surface d’une étoile

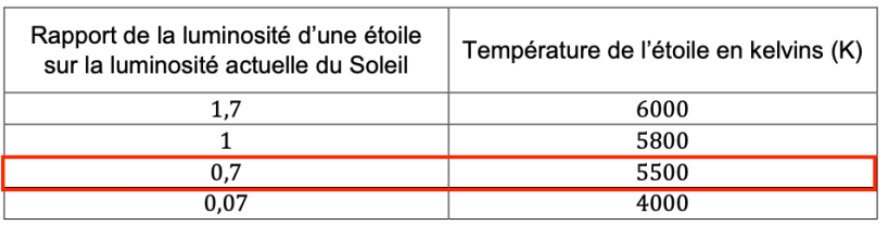
En astrophysique, le diagramme Hertzprung Russel permet d’établir une relation entre la température d’une étoile et sa luminosité et conduit aux correspondances précisées dans le tableau suivant :

Par exemple, si une étoile brille deux fois plus intensément que le Soleil actuel, ce rapport vaut 2.

Rapport de la luminosité d’une étoile sur la luminosité actuelle du Soleil	Température de l’étoile en kelvins (K)
1,7	6000
1	5800
0,7	5500
0,07	4000

Source : d’après l’auteur

Document 3 – Loi de Wien
La longueur d’onde d’intensité maximale (𝜆𝑚𝑎𝑥 exprimée en mètres) relevée sur un spectre d’émission est inversement proportionnelle à la température (T exprimée en kelvins) du corps émetteur :

$\lambda_{max}=\frac{k}{T}$

avec 𝑘, constante de la loi de Wien valant 2,99 × 10⁻³ K · m.

3- À l’aide des documents 2 et 3, déterminer en nanomètres la longueur d’onde d’intensité maximale du Soleil il y a 4 milliards d’années.

D’après l’énoncé, Il y a 4 milliards d’années, le Soleil ne brillait qu’à 70 % de son intensité actuelle.

La température de l’étoile était alors de 5500 kelvins (K).

A l’aide de la loi de Wien, calculons la longueur d’onde d’intensité maximale du Soleil il y a 4 milliards d’années :

$\lambda_{max,4m}=\frac{k}{T_{4m}}$

$\lambda_{max,4m}=\frac{2,99 \times {10}^{-3}}{5500}$

$\lambda_{max,4m}=5,44 \times {10}^{-7}m$

$\lambda_{max,4m}=544 \times {10}^{-9}m$

$\lambda_{max,4m}=544\ nm$

Il y a 4 milliards d’années, la longueur d’onde d’intensité maximale du Soleil était λmax = 544 nm .

Partie 2 – Première proposition d’explication du paradoxe

Document 4 – Tableau de la pression partielle atmosphérique en 𝐂𝐎_𝟐

Une température de −15 °C est incompatible avec la présence d’eau liquide. Des études ont permis de montrer qu’il y a 4 milliards d’années, un volcanisme très intense rejetait de grandes quantités de dioxyde de carbone dans l’atmosphère terrestre.

Période	−4 Milliards d’années	Actuelle
Pression partielle en 𝐂𝐎_𝟐	Entre 0,3 et 0,6 bar	3 × 10⁻⁴ bar

Source : d’après https://planet-terre.ens-lyon.fr

Document 5 – Bilan radiatif terrestre

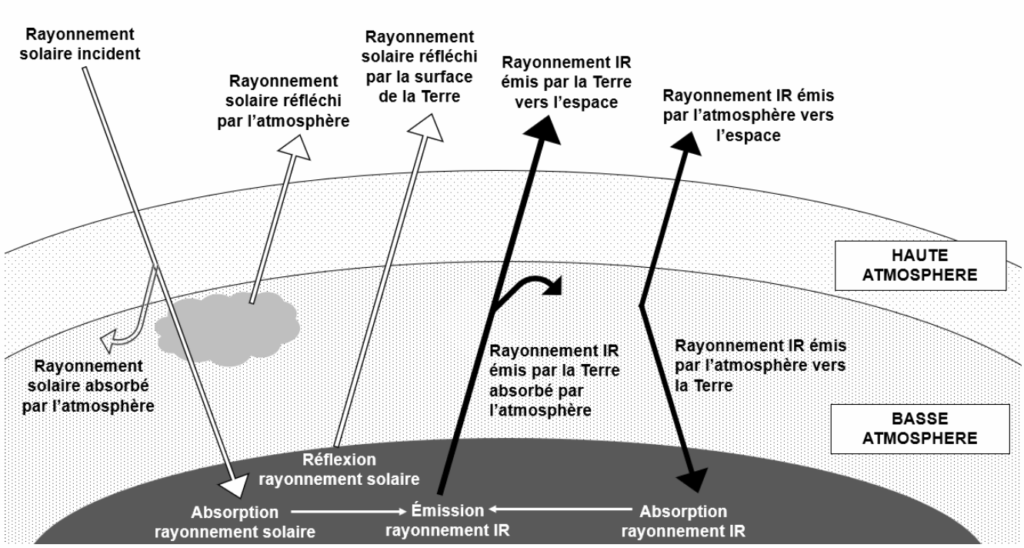
4- À partir des documents 4 et 5 et de vos connaissances, proposer une explication au paradoxe du Soleil pâle, c’est-à-dire à la présence d’eau liquide il y a 4 milliards d’années malgré une température terrestre inférieure à 0 °C due à la plus faible puissance reçue du Soleil.

La température calculée dans la partie 1 ne tient compte que du rayonnement reçu par la Terre en provenance du Soleil. Dans le document 5, présentant le bilan radiatif de la Terre, nous observons que la partie solide de la Terre et l’atmosphère jouent un rôle différencié. En effet, une partie du rayonnement solaire absorbé par la Terre est réémise par celle-ci sous forme d’infrarouges (IR) vers l’espace, mais aussi par la basse atmosphère qui l’absorbe.

Le document 4 nous indique que l’atmosphère terrestre, il y a 4 milliards d’années, contenait beaucoup plus de CO₂ (la pression partielle était 1000 à 2000 fois plus grande). Nous savons que le CO₂ est un gaz à effet de serre qui piège la chaleur émise par la Terre dans l’atmosphère, favorisant ainsi un réchauffement global. La présence importante de CO₂ permet donc à l’atmosphère de ne pas avoir une température trop faible, ce qui peut permettre la présence d’eau liquide.

Partie 3 – Seconde proposition d’explication du paradoxe

D’autres chercheurs ont proposé d’expliquer le paradoxe du Soleil jeune pâle par un albédo moyen très faible.

5 – Définir l’albédo.

L’albédo est une grandeur physique sans unité. Compris entre 0 et 1, il caractérise l’aptitude d’une surface à réfléchir le rayonnement qui lui parvient.

On le calcule en faisant le rapport entre la puissance réfléchie et la puissance incidente.

Document 6 – Quelques valeurs d’albédo

Surface	Océan	Forêt	Nuages	Sable	Neige
Albédo	0,05 – 0,10	0,05 – 0,10	0,2 – 0,3	0,2 – 0,3	0,8 – 0,9

Albédo moyen terrestre actuel : α = 0,3

Albédo moyen terrestre estimé à l’époque du Soleil jeune (4 milliards d’années) : α =0,05

Source : d’après l’auteur

6 – Expliquer pourquoi cette valeur permettrait d’expliquer la présence d’eau liquide sur Terre alors que la puissance surfacique solaire incidente était plus faible qu’actuellement.

L’albédo de la Terre était très faible, c’est-à-dire que la puissance réfléchie était faible et que la chaleur emmagasinée sur la Terre était importante, ce qui faisait monter la température globale et permettait d’avoir de l’eau liquide. En fait, l’albédo faible compensait la puissance solaire incidente plus faible.

9 – Expliquer en quoi l’étude de paradoxes scientifiques est une composante essentielle de la démarche scientifique. Vous argumenterez en vous appuyant sur l’exemple étudié dans cet exercice et sur vos connaissances personnelles.

La démarche scientifique est la suite d’étapes qu’utilisent les chercheurs pour trouver la solution à une problématique posée. Ici, la problématique est, d’une part, l’évidence de preuves indiquant la présence de vie sur Terre il y a 4 milliards d’années, ce qui suppose l’existence d’eau liquide et donc une température de plus de 0°C, une information venant des paléontologues. D’autre part, il y a l’information venant des astronomes indiquant que le Soleil était plus faible. Ces deux informations sont apparemment « contradictoires », il faut donc trouver « le chaînon » manquant pour résoudre le paradoxe. Nous avons une problématique à résoudre.

Il faut donc commencer par émettre des hypothèses, c’est-à-dire ici des conditions favorables à la présence d’eau liquide. Soit :

– La composition de l’atmosphère (GES favorable au réchauffement)

– La composition de la surface terrestre (ici, on suppose qu’il y a des océans et donc de l’eau liquide)

Pour chacune de ces hypothèses, il est nécessaire, avec les connaissances que nous avons actuellement, de vérifier comment elles solutionnent le paradoxe (c’est ce qui est fait dans cet énoncé), puis de les valider en cherchant des informations dans les diverses branches de la science.

Comme nous le voyons, résoudre les paradoxes permet de valider par plusieurs moyens les connaissances que nous avons actuellement, quitte à les infirmer et à les modifier si elles ne s’avèrent pas justes. Cela fait donc partie intégrante de la démarche scientifique.