Le parc de Yellowstone : un laboratoire grandeur nature pour l’étude des populations

Enseignement scientifique Terminale

Durée 1h – 10 points – Thème « Une histoire du vivant »

Le loup était autrefois le principal prédateur dans le célèbre parc national américain de Yellowstone, mais la population de loups a été éradiquée dans les années 1920. Tout l’écosystème a été modifié par cette disparition, en particulier la population de grands ongulés herbivores (élan, bison, cerf de Virginie, wapiti, antilope pronghorn, mouton d’Amérique et chèvre de montagne) dont l’expansion est devenue rapide. En 1995, 14 loups gris ont été réintroduits dans le parc de Yellowstone.

On cherche à comprendre les conséquences de cette réintroduction.

Partie 1- démographie des populations de loups et d’élans dans le parc de Yellowstone

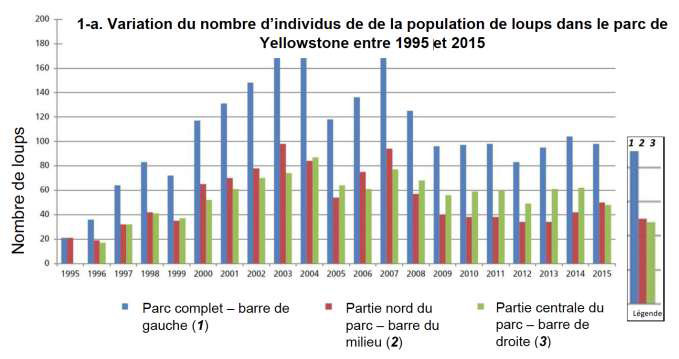
Document 1 : variation du nombre d’individus de la population de loups (a) et d’élans (b) dans le parc de Yellowstone depuis leur introduction jusqu’en 2015

1-b. Variation du nombre d’individus de la population d’élans en hiver dans la partie Nord du parc entre 1960 et 2015

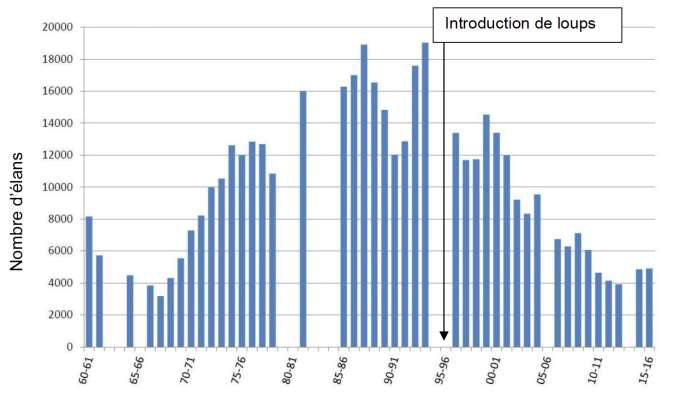
Les années sont indiquées par les deux derniers chiffres.

Clé de lecture :

• 60 – 61 : 1960 – 1061

• 00 – 01 : 2000 – 2001

Remarque : le comptage des élans n’a pas pu être effectué pendant certains hivers contrairement à celui des loups.

https://www.nps.gov/yell/learn/ys-24-1-wolf-restoration-in-yellowstone-reintroduction-to-recovery.htm

1. À partir de l’exploitation du document 1 mis en relation avec vos connaissances, répondre aux questions suivantes.

1.1. Entre une suite arithmétique et une suite géométrique, indiquer laquelle pourrait permettre de modéliser au mieux la variation globale du nombre d’individus de la population de loup durant les 8 premières années entre 1995 et 2003. (Aucun calcul n’est attendu)

Une suite est arithmétique s’il existe un nombre r tel que pour tout entier n, on a : u_(n+1)=u_n+r

Une suite est géométrique s’il existe un nombre q tel que pour tout entier n, on a : u_(n+1)=q×u_n

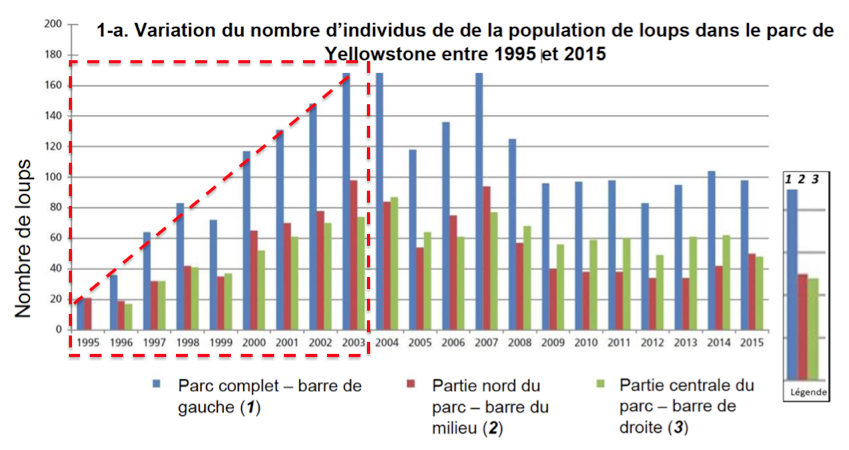
Globalement, entre 1995 et 2003, le nombre de loups augmente du même nombre d’individu chaque année

Une suite arithmétique pourrait permettre de modéliser au mieux la variation globale du nombre d’individus de la population de loup durant les 8 premières années entre 1995 et 2003.

1.2. Formuler une hypothèse permettant d’expliquer la variation du nombre d’individus de la population de loups depuis 2003.

La diminution de la diversité génétique est une hypothèse permettant d’expliquer la variation du nombre d’individus de la population de loups depuis 2003

Partie 2- Évolution génétique des populations de loups

Document 2 : étude génétique de la population de loups dans le parc de Yellowstone

La couleur du pelage des loups est liée à l’expression d’un gène qui existe sous deux formes : l’allèle K et l’allèle k. Les génotypes des loups ont été étudiés :

Génotype	(K//K)	(K//k)	(k//k)	Total
Nombre de loups	31	321	413	765
Couleur du pelage	Noir	Noir	Gris
Fréquence observée	0,04	0,42	0,54	1

On peut calculer la fréquence p de l’allèle K dans la population et la fréquence q de l’allèle k (q=1-p).

2. Expliquer en quoi les données du document 2 permettent de dire que la population actuelle n’est pas issue uniquement des loups gris introduits en 1995.

Pour un génotype (K//K) : le pelage est noir

Pour un génotype (k//k) : le pelage est gris

Pour un génotype (K//k) : le pelage est noir

Ainsi, le gène K est dominant.

Les loups gris introduits en 1995 comportent uniquement un génotype (k//k) .

Or les loups actuels sont noirs ou gris.

Ainsi, les données du document 2 permettent de dire que la population actuelle n’est pas issue uniquement des loups gris introduits en 1995.

3. Calculer les fréquences (notées p et q) de chacun des allèles du gène responsable de la couleur dans la population actuelle.

Génotype	(K//K)	(K//k)	(k//k)	Total
Nombre de loups	31	321	413	765
Couleur du pelage	Noir	Noir	Gris
Fréquence observée	0,04	0,42	0,54	1

p la fréquence de l’allèle K :

$p=\frac{\textrm{nombre d'individu possedant l'allèle K}}{\textrm{nombre d'individu total}}$

$p=\frac{\textrm{nombre de (K//K) + 1/2 nombre de (K//k) }}{\textrm{nombre d'individu total}}$

$p=\frac{31 + 1/2 \times 321 }{765}=0,25$

q la fréquence de l’allèle k :

$q=\frac{\textrm{nombre d'individu possedant l'allèle k}}{\textrm{nombre d'individu total}}$

$q=\frac{\textrm{nombre de (k//k) + 1/2 nombre de (K//k) }}{\textrm{nombre d'individu total}}$

$q=\frac{413 + 1/2 \times 321 }{765}=0,75$

On vérifie bien que

q=1-p

q=1-0,75

q=0,25

4. Indiquer sur votre copie la lettre correspondant à la proposition exacte :

Si la population de loups respecte le modèle de Hardy-Weinberg, à la génération suivante :

a La fréquence de l’allèle K sera plus élevée qu’actuellement.

b La fréquence de l’allèle k sera plus élevée qu’actuellement.

c La fréquence de chaque allèle restera constante.

d La fréquence des deux allèles n’est pas prévisible.

c La fréquence de chaque allèle restera constante.

5. En supposant que cette population respecte la loi de Hardy-Weinberg, calculer les fréquences génotypiques attendues à la génération suivante, en utilisant les données suivantes :

f(génotype K//K) = p²; f(génotype k//k) = q²; f(génotype K//k) = 2pq.

En supposant que cette population respecte la loi de Hardy-Weinberg, calculons les fréquences génotypiques attendues à la génération suivante :

f(génotype K//K) = p²

f(génotype K//K) = 0,25²

f(génotype K//K) = 0,0625

f(génotype k//k) = q²

f(génotype k//k) = 0,75²

f(génotype k//k) = 0,5625

f(génotype K//k) = 2pq

f(génotype K//k) = 2×0,25×0,75

f(génotype K//k) = 0,375

6. À partir du document 3, prouver que le modèle de Hardy-Weinberg n’est pas utilisable pour prévoir l’évolution de cette population de loups.

Document 3 : variation de la fréquence de l’allèle K (données issues du suivi des populations de loups entre 1996 et 2012)

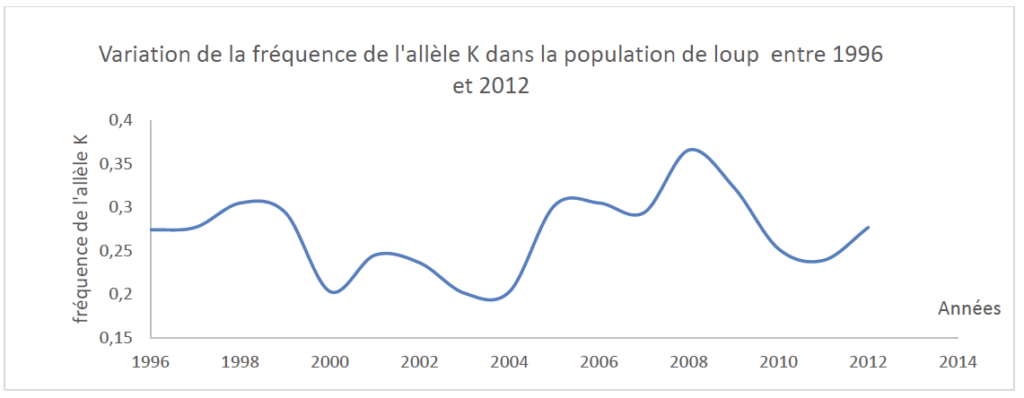
Données issues du « Journal of Heredity, Volume 105, Issue 4, July-August 2014, Pages 457–465 »

Couleur	Gris	Noir	Noir
Génotype	k//k	K//k	K//K
Taux de survie annuel * (en %)	75	77	47
Succès reproducteur moyen au cours de la vie ** (en nombre de descendants par individu)	1,83	2,35	0,031

* Le taux de survie annuel est égal au pourcentage d’individus survivants au bout d’un an.

** Le succès reproducteur correspond à la capacité d’un individu à diffuser ses gènes dans la population. Il se mesure par le nombre de ses descendants qui se reproduisent à leur tour.

À partir du document 3, calculons le nombre de descendants à la génération suivante :

Couleur	Gris	Noir	Noir
Génotype	k//k	K//k	K//K
Taux de survie annuel * (en %)	75	77	47
Succès reproducteur moyen au cours de la vie ** (en nombre de descendants par individu)	1,83	2,35	0,031
Nombre de descendants = Taux de survie annuel X Succès reproducteur moyen au cours de la vie	75×1,83=137	77×2,35=181	47×0,031=1,5

À partir du document 3, calculons les fréquences génotypiques réelles à la génération suivante :

$\textrm{f(génotype K//K)}=\frac{\textrm{nombre d'individu possedant le génotype K//K}}{\textrm{nombre d'individu total}}$

$\textrm{f(génotype K//K)}=\frac{1,5}{137+181+1,5}$

$\textrm{f(génotype K//K)}=0,00469$

$\textrm{f(génotype k//k)}=\frac{\textrm{nombre d'individu possedant le génotype k//k}}{\textrm{nombre d'individu total}}$

$\textrm{f(génotype k//k)}=\frac{137}{137+181+1,5}$

$\textrm{f(génotype k//k)}=0,429$

$\textrm{f(génotype K//k)}=\frac{\textrm{nombre d'individu possedant le génotype K//k}}{\textrm{nombre d'individu total}}$

$\textrm{f(génotype K//k)}=\frac{181}{137+181+1,5}$

$\textrm{f(génotype K//k)}=0,567$

Comparons les fréquences génotypiques attendues à la génération suivante issue de la loi de Hardy-Weinberg et les fréquences réelles :

	Fréquences issue de la loi de Hardy-Weinberg	fréquences réelles	Concordance
génotype K//K	0,0625	0,00469	Non
génotype k//k	0,5625	0,429	Non
génotype K//k	0,375	0,567	Non

Les fréquences génotypiques attendues à la génération suivante issue de la loi de Hardy-Weinberg et les fréquences réelles ne sont pas identiques. Ainsi, le modèle de Hardy-Weinberg n’est pas utilisable pour prévoir l’évolution de cette population de loups.