Le projet SEAREV : Système Électrique Autonome de Récupération de l’Énergie des Vagues

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH102 et n°SPEPHCH112

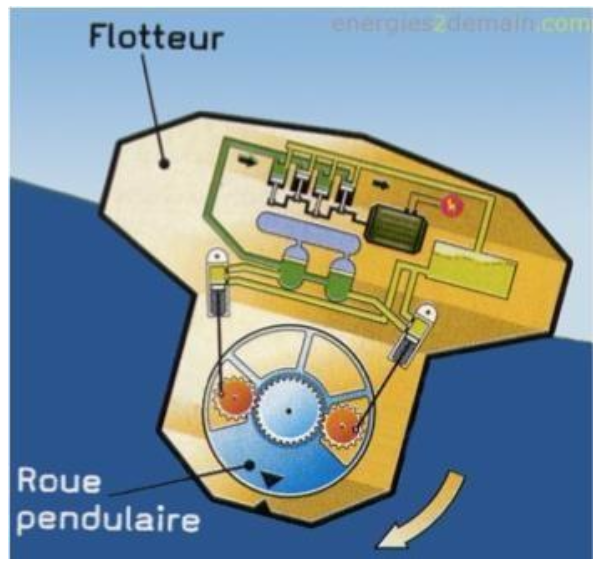
Comment fonctionne le système SEAREV ? SEAREV est un système offshore de deuxième génération composé d’un flotteur clos et étanche dans lequel est suspendue une roue chargée qui joue le rôle d’un pendule embarqué. Cette roue à axe horizontal, de grand diamètre (9 m), dont la moitié supérieure est évidée, a sa masse concentrée dans la moitié inférieure, lestée de béton, d’où l’effet de pendule. Sous l’action de la houle et des vagues, le flotteur se met à osciller, entraînant à son tour un mouvement de va-et-vient de la roue pendulaire. Chacun a son propre mouvement, et c’est le mouvement relatif entre le flotteur et la roue qui actionne un système hydro-électrique de conversion de l’énergie mécanique en électricité : des pompes hydrauliques liées à la roue pendulaire chargent des accumulateurs à haute pression ; en se déchargeant, ces derniers livrent à leur tour leur énergie à des moteurs hydrauliques qui entraînent des générateurs d’électricité. Plusieurs flotteurs SEAREV mouillés au large forment un parc (ou ferme). L’électricité est ramenée à terre par un câble sous-marin.

http://www2.cnrs.fr/sites/communique/fichier/08searev.pdf

Pour comprendre le fonctionnement complexe de la roue pendulaire du SEAREV, il a fallu s’intéresser aux oscillations libres des systèmes. Dans cet exercice, la roue pendulaire est modélisée par un pendule simple composé d’une bille de masse m et d’un fil de longueur L. On considère que la roue pendulaire, au passage d’une vague, effectue une oscillation complète (soit un aller-retour).

Schéma d’un module SEAREV

www.energies2demain.com

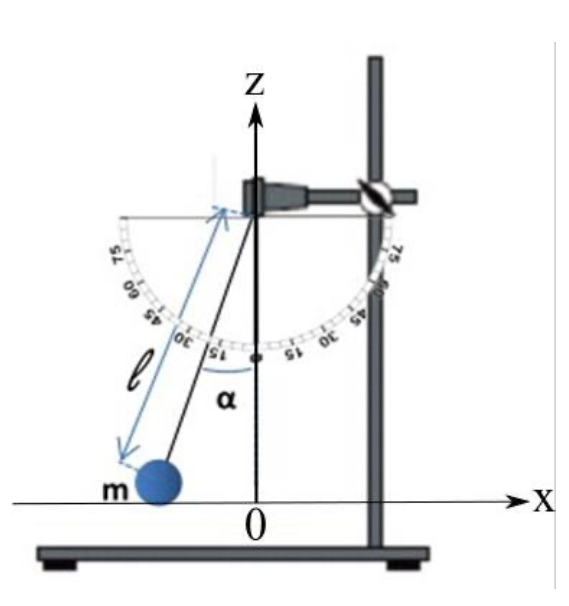
Schéma d’un pendule simple

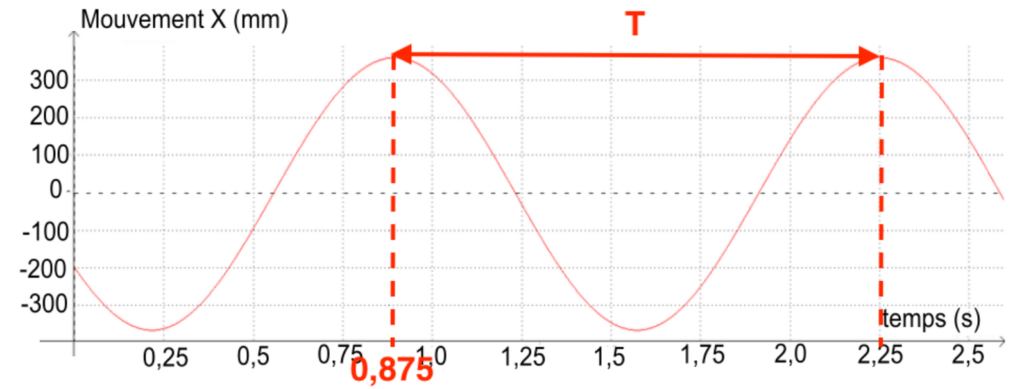
Afin d’étudier le pendule simple, une vidéo enregistrant les oscillations du pendule a été réalisée ainsi que le pointage des positions occupées par le pendule au cours du temps. On obtient la courbe présentée ci-après.

Oscillations du pendule simple

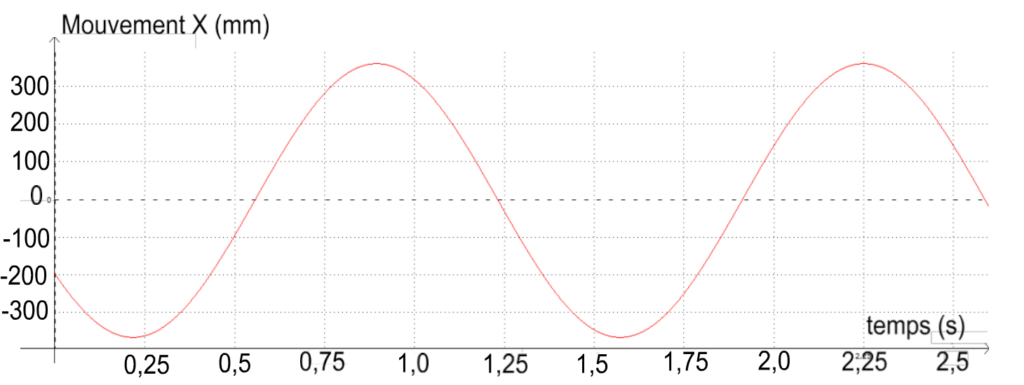
1. Déterminer la valeur de la période des oscillations du pendule simple étudié.

T=2,25-0,875
T=1,38 s

La période des oscillations du pendule simple étudié a pour valeur 1,375 s.

2. En déduire celle de la fréquence des oscillations de ce pendule.

$\mathrm{ f = \frac{1}{T}}$

$\mathrm{ f = \frac{1}{1{,}38}}$

$\mathrm{ f = 0{,}72 \, \text{Hz}}$

3. On considère que des vagues atteignent un module SEAREV à un rythme constant. On modélise la roue pendulaire par le pendule simple étudié ci-dessus. Calculer le nombre de vagues qui atteindraient le module en 50 secondes. Commenter le résultat obtenu.

1 vague	1,38 s
N vagues	50 s

$\mathrm{ N = \frac{1 \times 50}{1{,}38}}$

$\mathrm{ N = 36}$

Si on considère que des vagues atteignent un module SEAREV à un rythme constant, 36 vagues atteindraient le module en 50 secondes.

Les nombre de vague est important au vu du temps dans lequel elles arrivent.

L’énergie des vagues

On considère la puissance moyenne annuelle transportée par mètre perpendiculaire à la direction de propagation des vagues. Les valeurs maximales à la surface du globe, 100 kW·m^-1, se trouvent au Cap Horn, alors que dans le Golfe de Gascogne en face de nos côtes, on trouve des niveaux de 40 kW·m^-1. La ressource moyenne globale en puissance des vagues se situerait entre 1,3 et 2 TW (soit entre 1,3.10¹² et 2.10¹² W) d’après le World Energy Council, soit l’ordre de grandeur de la puissance électrique mondiale installée (~2 TW). L’énergie récupérable avec les moyens envisagés aujourd’hui serait de l’ordre de 140 à 750 TWh par an. Les développeurs estiment que l’on pourrait installer en mer des parcs de machines avec une densité de puissance de l’ordre de 25 MW par km² de mer occupée, ce qui pourrait alimenter de 7 000 à 8 000 foyers français en électricité (moyenne annuelle hors chauffage). http://www2.cnrs.fr/sites/communique/fichier/08searev.pdf

4. Indiquer si le module SEAREV est un convertisseur d’énergie. Justifier.

Le module SEAREV reçoit de l’énergie mécanique et délivre de l’énergie électrique : le module SEAREV est un convertisseur d’énergie.

Afin de mieux comprendre l’aspect énergétique du module SEAREV, on étudie les énergies associées aux oscillations d’un pendule simple. On obtient les courbes simulées ci-après représentant les variations des énergies cinétique, potentielle et mécanique d’un pendule simple.

5. Un joule équivaut à un kg∙m²∙s^-2. Parmi les expressions suivantes, choisir, en justifiant à l’aide d’une analyse des unités, celle de l’énergie cinétique 𝐸_𝐶 puis celle de l’énergie potentielle de pesanteur 𝐸_𝑃𝑃.

a) $Ec=\frac{1}{2}\times m \times v^2$

b) $Ec=\frac{1}{2}\times m \times v$

c) $Ec=\frac{1}{2} \times v^2$

d) $Epp=m \times g$

e) $Epp=m \times g \times z$

f) $Epp= g \times z$

où 𝑚 est la masse du système étudié, 𝑣 est la vitesse, 𝑔 est l’intensité de la pesanteur et 𝑧 l’altitude.

$\mathrm{E_c = \frac{1}{2} \times m \times v^2}$

$\mathrm{[E_c] = \left[\frac{1}{2}\right] \times [m] \times [v]^2}$

$\mathrm{\text{J} = \text{kg} \cdot (\text{m} \cdot \text{s}^{-1})^2}$

$\mathrm{\text{J} = \text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}}$

Vrai

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est correcte au vu de l’analyse des unités.

$\mathrm{E_c = \frac{1}{2} \times m \times v}$

$\mathrm{[E_c] = \left[\frac{1}{2}\right] \times [m] \times [v]}$

$\mathrm{\text{J} = \text{kg} \cdot \text{m} \cdot \text{s}^{-1}}$

Faux

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est fausse au vu de l’analyse des unités.

$\mathrm{E_c = \frac{1}{2} \times v^2}$

$\mathrm{[E_c] = \left[\frac{1}{2}\right] \times [v]^2}$

$\mathrm{\text{J} = (\text{m} \cdot \text{s}^{-1})^2}$

$\mathrm{\text{J} = \text{m}^2 \cdot \text{s}^{-2}}$

Faux

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est fausse au vu de l’analyse des unités.

$\mathrm{E_{pp} = m \times g}$

$\mathrm{[E_{pp}] = [m] \times [g]}$

$\mathrm{\text{J} = \text{kg} \cdot \text{m} \cdot \text{s}^{-2}}$

Faux

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est fausse au vu de l’analyse des unités.

$\mathrm{E_{pp} = m \times g \times z}$

$\mathrm{[E_{pp}] = [m] \times [g] \times [z]}$

$\mathrm{\text{J} = \text{kg} \cdot \text{m} \cdot \text{s}^{-2} \cdot \text{m}}$

$\mathrm{\text{J} = \text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}}$

Vrai

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est correcte au vu de l’analyse des unités.

$\mathrm{E_{pp} = g \times z}$

$\mathrm{[E_{pp}] = [g] \times [z]}$

$\mathrm{\text{J} = \text{m} \cdot \text{s}^{-2} \cdot \text{m}}$

$\mathrm{\text{J} = \text{m}^2 \cdot \text{s}^{-2}}$

Faux

L’énoncé nous indique que « un joule équivaut à un $\text{kg} \cdot \text{m}^2 \cdot \text{s}^{-2}$ » : l’expression proposée est fausse au vu de l’analyse des unités.

Simulation des variations des énergies cinétique, potentielle et mécanique d’un pendule simple

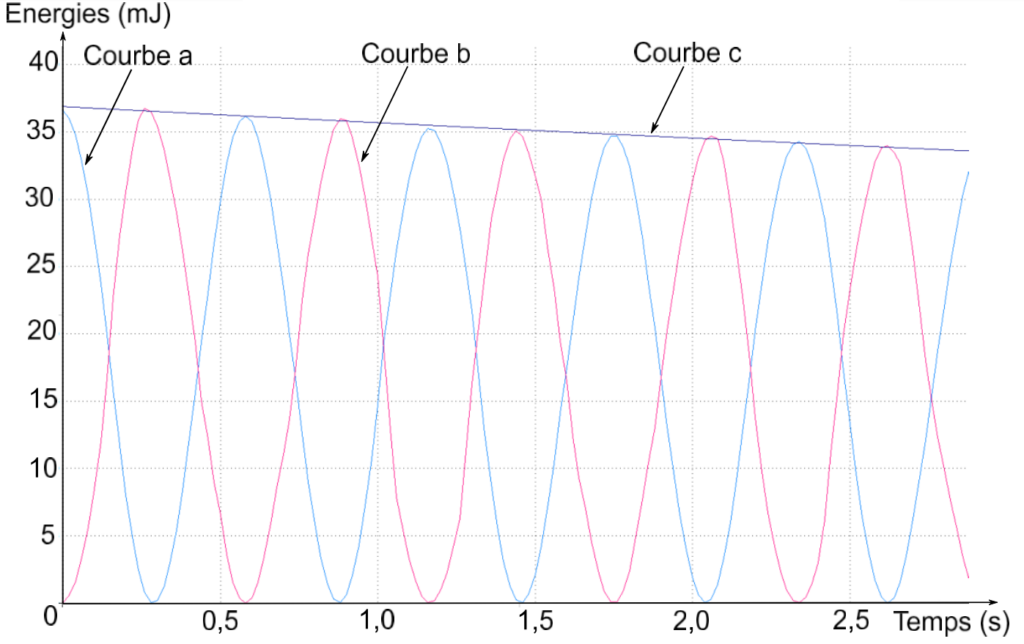
6. Le pendule est lâché, sans vitesse initiale, avec un angle α = 30°. Associer à chaque courbe (a, b et c) de la simulation, une énergie (cinétique, potentielle ou mécanique). Justifier.

Em =Ec +Epp : l’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur. La courbe la représentant est la somme des deux autres : courbe c

Ec =1/2×m×v² : Le pendule est lâché, sans vitesse initiale. Ainsi, à l’instant initiale, la vitesse étant nulle, l’énergie cinétique est nulle : courbe b

Epp = m × g × z : l’énergie potentielle de pesanteur est proportionnelle à l’altitude. Le pendule est lâché, avec un angle α=30°. L’altitude initiale n’est pas nulle. L’énergie potentielle initiale Epp n’est pas nulle : Courbe a

7. Indiquer si l’énergie mécanique du pendule est conservée au cours de son mouvement. Justifier.

L’énergie mécanique (courbe c) du pendule diminue au cours du temps. Ainsi, l’énergie mécanique n’est pas conservée au cours de son mouvement.

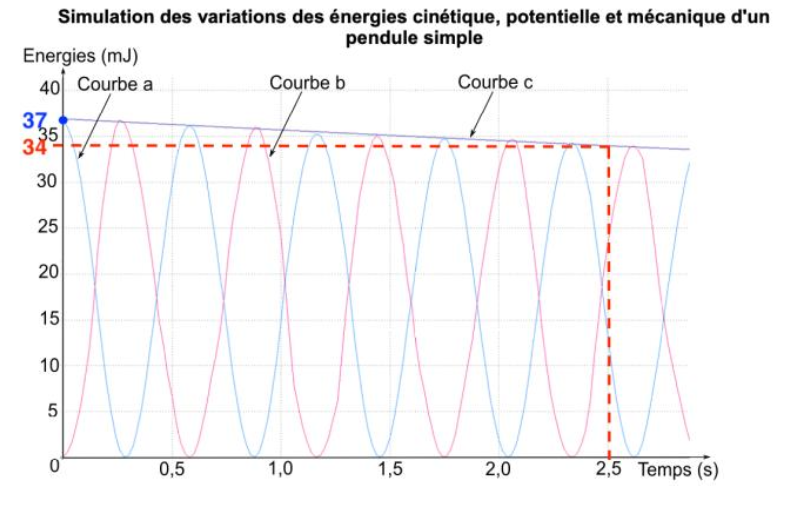
8. Déterminer la valeur du travail des forces non conservatives s’exerçant sur le pendule pendant une durée Δt = 2,5 s. Justifier.

$\mathrm{\Delta E_m = W_{BC}(\vec{F}_{\text{non conservatives}})}$

$\mathrm{W_{BC}(\vec{F}_{\text{non conservatives}}) = \Delta E_m}$

$\mathrm{W_{BC}(\vec{F}_{\text{non conservatives}}) = E_m(t = 2{,}5 \, \text{s}) - E_m(t = 0 \, \text{s})}$

Graphiquement, on obtient :

$\mathrm{E_m(t = 2{,}5 \, \text{s}) = 34 \, \text{mJ}}$

$\mathrm{E_m(t = 0 \, \text{s}) = 37 \, \text{mJ}}$

Ainsi :

$\mathrm{W_{BC}(\vec{F}_{\text{non conservatives}}) = 34 \, \text{mJ} - 37 \, \text{mJ}}$

$\mathrm{W_{BC}(\vec{F}_{\text{non conservatives}}) = -3{,}0 \, \text{mJ}}$

9. Citer une force non conservative s’exerçant sur un module SEAREV.

La force de frottement est une force non conservative s’exerçant sur un module SEAREV.

Des parcs de machines composés de dizaines de module SEAREV sont envisagés pour produire de l’électricité. On estime la surface d’un parc de machine à 1 km². D’après le site futura-science.com, la consommation d’électricité annuelle moyenne par foyer en France est d’environ 5 MWh.

10. Déterminer si un parc de machines permettrait de répondre aux besoins énergétiques annuels de 8000 foyers français, comme indiqué précédemment.

Donnée : 1 Wh = 3 600 J.

La consommation d’électricité annuelle moyenne par foyer en France est d’environ 5 MWh.

Calculons la consommation d’électricité annuelle moyenne de 8 000 foyers français :

$\mathrm{ E_{8000} = 5 \times 10^6 \times 8000}$

$\mathrm{ E_{8000} = 4 \times 10^{10} \, \text{Wh}}$

D’après l’énoncé : « Les développeurs estiment que l’on pourrait installer en mer des parcs de machines avec une densité de puissance de l’ordre de 25 MW par km² »

Calculons l’énergie annuelle produite par un parc de machine à 1 km² :

$\mathrm{ E_{\text{produite}} = P_{\text{produite}} \times \Delta t}$

Remarque : en mettant le temps (une année ici) en heures, on obtient des Wh.

$\mathrm{ E_{\text{produite}} = 25 \times 10^6 \times 1 \times 365{,}25 \times 24}$

$\mathrm{ E_{\text{produite}} = 2{,}2 \times 10^{11} \, \text{Wh}}$

L’énergie annuelle produite par un parc de machine à 1 km² est supérieure à la consommation d’électricité annuelle moyenne de 8 000 foyers français.

Ainsi, un parc de machines permettrait de répondre aux besoins énergétiques annuels de 8 000 foyers français, comme indiqué précédemment.