Sujet avec enseignement de mathématiques spécifique
Enseignement scientifique première
Durée 1h12 – 12 points – Thème « Le Soleil, notre source d’énergie »
Sujet n°ENSSCIMAT163, n°ENSSCIMAT175 et n°ENSSCIMAT178
Télécharger l’exercice en PDF :
L’expression « Le sang des glaciers » désigne le rosissement des glaciers par une espèce d’algues des neiges. Nous nous intéresserons dans une première partie à l’énergie solaire reçue par la Terre et au phénomène de l’albédo, puis dans une seconde partie nous chercherons à comprendre en quoi ce type d’algues peut contribuer au réchauffement climatique.
Partie A – Comprendre l’albédo
Document 1 – Modélisation permettant le calcul de la puissance rayonnée
À une distance donnée du Soleil, la totalité de la puissance émise par le Soleil se trouve uniformément répartie sur une sphère de rayon égal à cette distance.
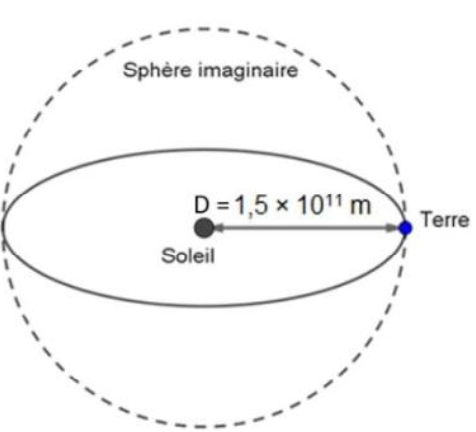
La puissance surfacique 𝑃𝑆 reçue par chaque point de la sphère imaginaire est donc donnée par la formule suivante :
$$P_S=\frac{P_T}{S}$$
, exprimée en W · m−2
Avec 𝑃𝑇 la puissance totale du soleil qui vaut 3,87 × 1026 W et 𝑆 la surface de la sphère imaginaire.
Sur le schéma ci-contre, la Terre et le Soleil ne sont pas représentés à l’échelle.
On rappelle que l’aire d’une sphère de rayon 𝑅 est 𝑆𝑠𝑝ℎè𝑟𝑒 = 4𝜋𝑅2 et que l’aire d’un disque de rayon 𝑅 est 𝑆𝑑𝑖𝑠𝑞𝑢𝑒 = 𝜋𝑅2.
1 – À partir de vos connaissances, nommer le phénomène physique à l’origine de l’énergie dégagée par le Soleil.
Le phénomène physique à l’origine de l’énergie dégagée par le Soleil est la fusion nucléaire : des noyaux d’hydrogène se combinent pour former de l’hélium.
2 – Montrer par le calcul, à l’aide du document 1, que la puissance solaire 𝑃𝑆 reçue par mètre carré à la distance 𝐷 du Soleil est environ de 1 370 W ∙ m−2.
$$P_S=\frac{P_T}{S}$$
Avec $S=4\pi R^2$
$$P_S=\frac{P_T}{4\pi R^2}$$
$$P_S=\frac{3,87 \times {10}^{26}}{4\pi{ \times \left(1,5 \times {10}^{11}\right)}^2}$$
$$P_S=1369\ W.m^{-2}$$
La puissance solaire PS reçue par mètre carré à la distance 𝐷 du Soleil est environ de 1 370 W.m−2.
3 – La Terre intercepte le rayonnement solaire sur une surface correspondant à un disque de rayon 𝑅 = 6 400 km. Calculer l’aire de cette surface, exprimée en m2.
D’après le document 1 : l’aire d’un disque de rayon 𝑅 est 𝑆𝑑𝑖𝑠𝑞𝑢𝑒 = 𝜋𝑅2.
$$S=\pi R^2$$
$$S=\pi \left(6400 \times {10}^3\right)^2$$
$$S=1,287 \times {10}^{14}m^2$$
4 – La puissance surfacique solaire correspond à la puissance solaire reçue par une surface d’un mètre carré. Montrer par le calcul que la puissance solaire 𝑃reçue reçue par la Terre d’après ce modèle simplifié est voisine de 1,8 × 1017 W.
La puissance surfacique solaire correspond à la puissance solaire reçue par une surface d’un mètre carré. Soit :
$$P_S=\frac{P_{recue}}{S}$$
$$\frac{P_{recue}}{S}=P_S$$
$$P_{recue}=P_S \times S$$
$$P_{recue}=1369 \times 1,287 \times {10}^{14}$$
$$P_{recue}=1,762 \times {10}^{17}\ W$$
Ainsi, la puissance solaire Preçue reçue par la Terre d’après ce modèle simplifié est voisine de 1,8 × 1017 W.
5 – La puissance solaire moyenne reçue par la Terre se répartit sur toute la surface de la sphère qu’elle constitue : $P_{moy}=\frac{P_{recue}}{S_{Terre}}$ . Montrer que la puissance solaire moyenne reçue par unité de surface vaut 342 W · m−2.
$$P_{moy}=\frac{P_{recue}}{S_{Terre}}$$
Avec $S_{Terre}=4\pi R_{Terre}^2$
$$P_{moy}=\frac{P_{recue}}{4\pi R_{Terre}^2}$$
$$P_{moy}=\frac{1,762 \times {10}^{17}}{4\pi { \times \left(6400 \times {10}^3\right)}^2}$$
$$P_{moy}=342\ W.m^{-2}$$
Ainsi, la puissance solaire moyenne reçue par unité de surface vaut 342 W·m−2.
Document 2 – Bilan radiatif
La puissance solaire qui est reçue par la Terre peut être réfléchie, absorbée, réémise.
Le schéma ci-dessous présente les flux énergétiques émis, diffusés et réfléchis par les différentes parties de l’atmosphère et de la surface terrestre.
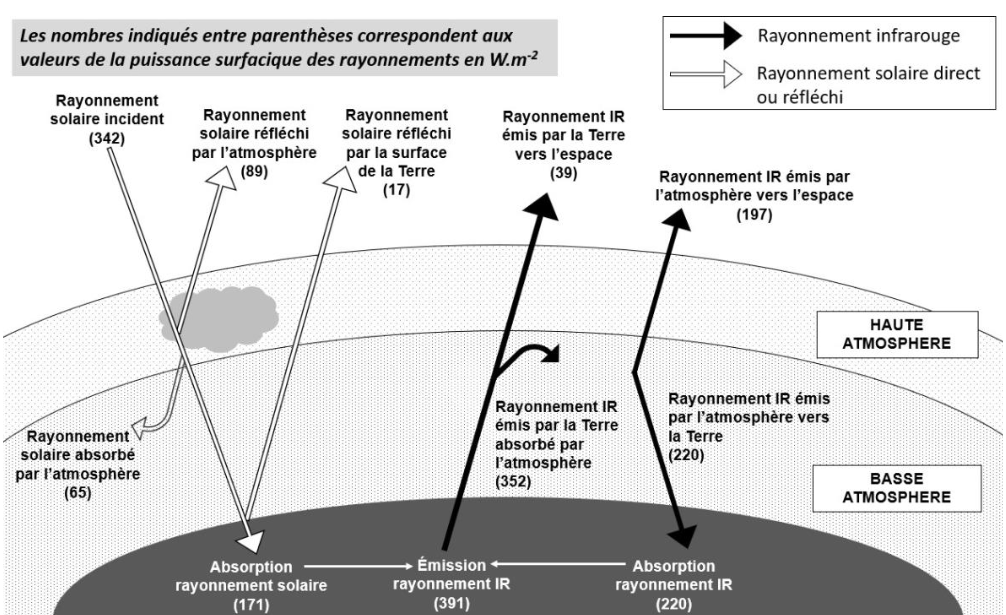
Source : d’après l’auteur
Document 3 – Albédo
L’albédo A d’une surface permet d’évaluer l’effet de réflexion de la lumière incidente par une surface. C’est le rapport entre la puissance de rayonnement réfléchie par une surface (P réfléchie) et la puissance de rayonnement incident sur cette même surface
(P incidente).
L’albédo A est une valeur sans unité, comprise entre 0 et 1.
$$A=\frac{P_{reflechie}\ (W.m^{-2})}{P_{incidente}(W.m^{-2})}$$
Moins le rayonnement incident est réfléchi, plus la surface chauffe.
Source : https://planet-terre.ens-lyon.fr
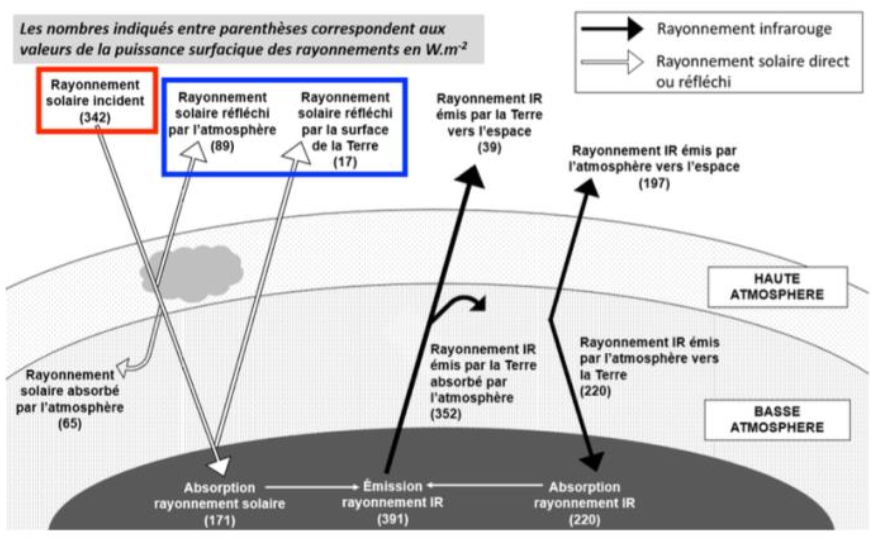
6 – À l’aide des documents 2 et 3, montrer que l’albédo terrestre moyen qui correspond à l’albédo de l’ensemble {atmosphère + surface de la Terre} vaut environ 0,3.
D’après le Document 2 :
$$P_{reflechie}=89+17$$
$$P_{reflechie}=106\ W.m^{-2}$$
$$P_{incidente}=342\ W.m^{-2}$$
D’après le Document 3 :
$$A=\frac{P_{reflechie}}{P_{incidente}}$$
$$A=\frac{106}{342}$$
A=0,31
Ainsi, l’albédo terrestre moyen qui correspond à l’albédo de l’ensemble {atmosphère + surface de la Terre} vaut environ 0,3.
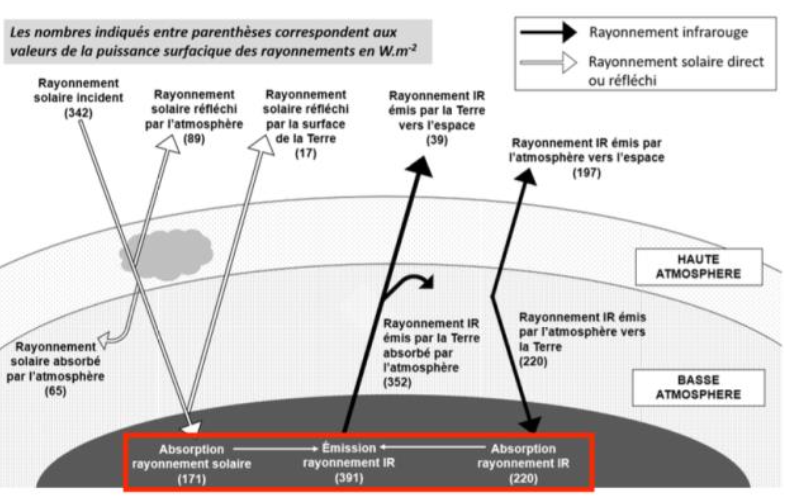
7 – À l’aide du document 2, justifier à l’aide de calculs que le bilan radiatif terrestre est équilibré.
Bilan radiatif terrestre :
- Energie absorbée : 391 W.M-2
- Rayonnement solaire 171 W.M-2
- Rayonnement IR absorbé 220 W.M-2
- Energie émise : 391 W.M-2
- Rayonnement IR émis 391 W.M-2
L’énergie absorbée est égale à l’énergie émise : le bilan radiatif terrestre est équilibré.
8 – En vous appuyant sur les documents 2 et 3 et sur vos connaissances, citer deux phénomènes qui peuvent contribuer à déséquilibrer ce bilan et entrainer un réchauffement climatique. Justifier votre réponse.
Deux phénomènes qui peuvent contribuer à déséquilibrer le bilan climatique et entraîner un réchauffement climatique sont :
- La diminution des surface claires. D’après le document 3 : Moins le rayonnement incident est réfléchi, plus la surface chauffe. Les surfaces claires réfléchissent le rayonnement reçu. Leur diminution entraine une diminution du rayonnement réfléchi donc un réchauffement climatique.
- Les émissions de gaz à effet de serre : Ces gaz augmentent la part du rayonnement absorbé et ainsi contribuent au réchauffement climatique.
Partie B – Origine et conséquences de la couleur rose des glaciers
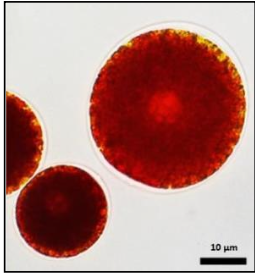
Les algues des neiges sont des algues unicellulaires capables de vivre à une température d’environ 0 °C. La plus courante d’entre elles est la Chlamydomonas nivalis (observée au microscope optique sur la photographie ci- contre). C’est une algue verte qui en plus de la chlorophylle, contient un pigment rouge de type caroténoïde à l’origine de la coloration rose-clair des glaciers. Cet organisme, d’une teinte rose-clair, remonte à la surface, en été, pour pouvoir accéder à l’eau liquide et se multiplie activement.
Source : d’après https://www.semanticscholar.org/
Document 4 – Identification du métabolisme de cet organisme
De la glace rose contenant des Chlamydomonas nivalis est fondue et placée dans une enceinte hermétique. Les teneurs en dioxygène et en dioxyde de carbone dans l’eau sont relevées sous différentes conditions d’éclairement. Le graphique ci-dessous présente l’évolution des teneurs en dioxygène et dioxyde de carbone dans de l’eau contenant Chlamydomonas nivalis.
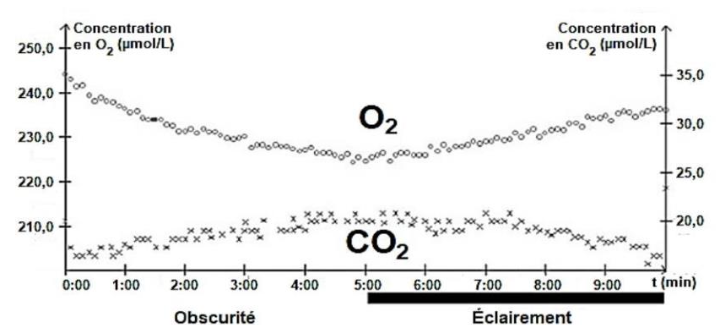
Source : Bac S SVT 2017 Afrique
9 – À partir de l’étude du document 4 et de vos connaissances, montrer que Chlamydomonas nivalis est un organisme photosynthétique.
Le document 4 nous montre qu’en présence de lumière, la concentration en CO2 diminue et celle de O2 augmente. La Chlamydomonas nivalis transforme le CO2 en O2 en présence de lumière :
Chlamydomonas nivalis est donc un organisme photosynthétique.
Document 5 – Mesure de l’albédo de glace présentant différentes teintes
On a mesuré l’albédo de la glace non colorée ainsi que de la glace colorée par différents colorants.
| Surface | Albédo |
| Glace non colorée | 0,60 |
| Glace rose | 0,42 |
| Glace verte | 0,52 |
| Glace bleue | 0,48 |
Source : D’après l’auteur
10 – D’après l’étude des documents 3 et 5, expliquer en quoi la présence de Chlamydomonas nivalis peut être une menace pour les glaciers d’altitude.
L’albédo de la glace non colorée est de 0,60 tandis que pour une surface rose l’albédo est de 0,42.
Plus l’albédo est faible, plus la surface absorbe l’énergie du rayonnement.
Ainsi, la présence de Chlamydomonas nivalis colore la neige : elle est la cause d’une augmentation de l’absorption d’énergie solaire ce qui accélère la fonte.
Ainsi, la présence de Chlamydomonas nivalis peut être une menace pour les glaciers d’altitude.
11 – Ce type d’algues de neige s’observe également au niveau des zones polaires. Justifier le fait que les algues des neiges peuvent contribuer au réchauffement climatique.
Comme mentionné dans la question précédente, la présence de Chlamydomonas nivalis colore la neige, réduisant ainsi son albédo. Lorsque l’albédo diminue, l’absorption de l’énergie solaire augmente. Par conséquent, les algues des neiges peuvent contribuer au réchauffement climatique.
