ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée
Sujet 2024 n°SPEPHCH105 et n°SPEPHCH113
Télécharger l’exercice en PDF :
Document 1 : Le saut pendulaire
Dix secondes de chute libre depuis une falaise qui offre plus de 400 mètres de vide, ça vous dit quelque chose ?
C’est le temps et le nouveau record de France réalisé en rope jump, dernier né des sports extrêmes qui s’inspire à la fois du base jump et du saut à l’élastique. Sauf que dans cette discipline (le saut pendulaire en bon français), les athlètes ne sont pas attachés par un élastique mais par de simples cordes d’alpinisme… Et la longueur de chute libre atteint 80 % de la hauteur quand le saut à l’élastique limite la chute proprement dite à 40 %.
D’après le dauphiné libéré https://www.ledauphine.com/isere-sud/2019/09/15/
Document 2 : Les différentes phases du saut
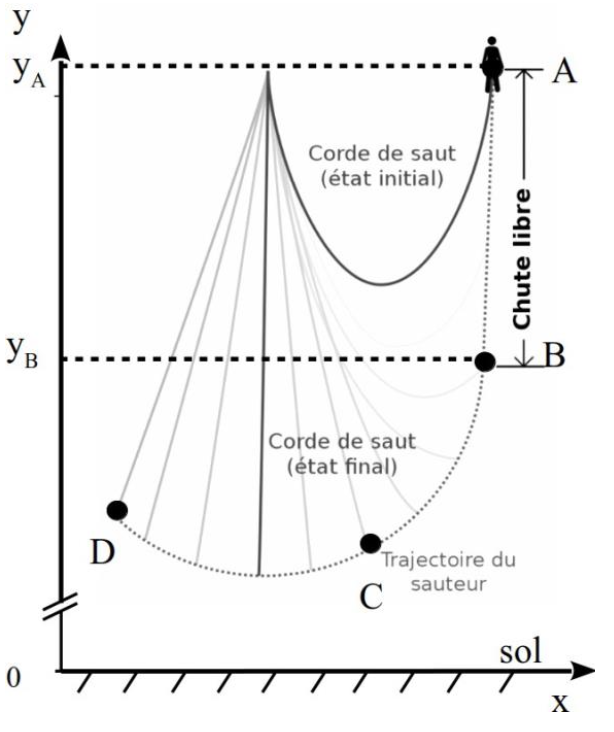
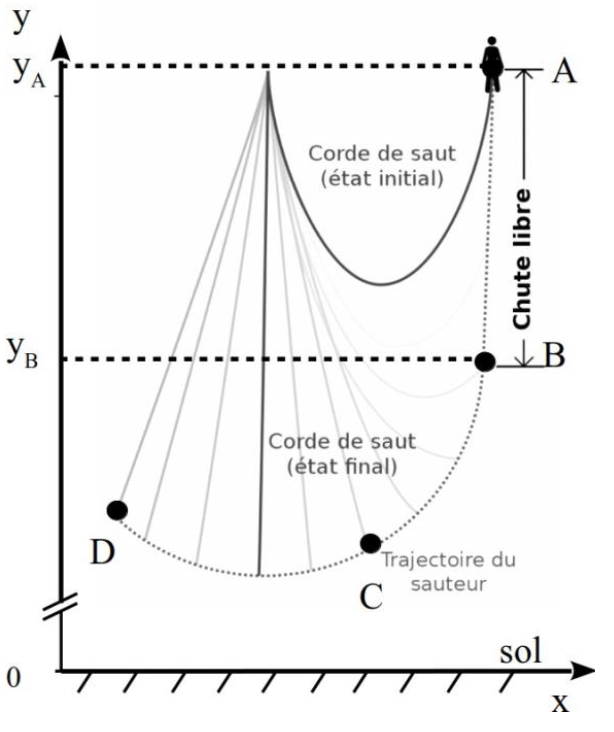
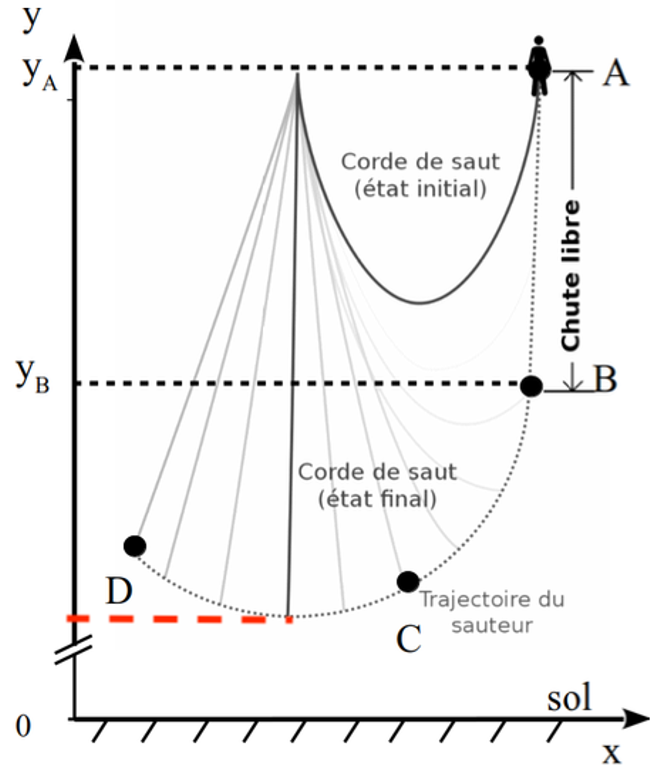
Le saut pendulaire peut se décomposer en trois phases :
- la première, entre A et B est une phase de chute libre où la corde n’est pas tendue ;
- la deuxième, entre B et C, la corde commence à se tendre et la trajectoire du sauteur est déviée sous son action ;
- la dernière, entre C et D, la corde est tendue et la trajectoire du sauteur est circulaire.
Pour repérer l’altitude du sauteur, on utilise un axe des y vertical dont l’origine est au sol.
Document 3
Le but de cet exercice est de vérifier que la hauteur de chute libre lors d’un saut pendulaire correspond à 80 % de la hauteur du saut, c’est à dire la longueur de la corde.
Pour cela, on étudie l’enregistrement vidéo d’un saut réalisé par un sauteur de masse m = 80,0 kg (avec son équipement). Un pointage vidéo a été réalisé, il a permis d’obtenir les coordonnées (x,y) du sauteur au cours du temps.
Le sautoir se situe à une altitude yA = 30 m par rapport au sol.
Donnée : intensité du champ de pesanteur : g = 9,81 m.s-2.
1. Étude de la première phase du saut entre A et B
1.1 Étude du saut en négligeant les frottements
Dans un premier temps, on formule l’hypothèse que les forces de frottement de l’air sont négligeables.
1.1.1. Effectuer l’inventaire des forces extérieures appliquées au système.
Entre A et B est une phase de chute libre où la corde n’est pas tendue. La corde n’exerce pas de force sur le système.
De plus, on formule l’hypothèse que les forces de frottement de l’air sont négligeables.
Les forces s’exerçant sur le système entre A et B sont :
– Le poids \(\ overrightarrow{P}\)
1.1.2. Donner l’expression du travail du poids $W_{AB}\left ( \overrightarrow{P} \right )$ entre les points A et B en fonction de m, g, yA et yB, altitude du point B. Ce travail est-il moteur ou résistant ?
\[ \mathrm{ W_{AB}(\vec{P}) = m \times g \times (y_A – y_B) }\]
Puisque \( y_A > y_B \), donc \( (y_A – y_B) > 0 \).
Ainsi, \( W_{AB}(\vec{P}) > 0 \) : le travail du poids est moteur.
1.1.3. On considère que la vitesse initiale du sauteur au point A est nulle. En utilisant le théorème de l’énergie cinétique entre les points A et B, montrer que 𝑉𝐵 la vitesse au point B est reliée à la hauteur de chute libre h = (yA – yB) par la relation : $V_{B}=\sqrt{2gh}$.
Théorème de l’énergie cinétique entre A et B :
\[ \mathrm{ \Delta E_c = \sum W_{BC}(\vec{F})}\]
\[ \mathrm{ E_c(B) – E_c(A) = W_{BC}(\vec{P})}\]
\[ \mathrm{ \frac{1}{2} \times m \times v_B^2 – \frac{1}{2} \times m \times v_A^2 = m \times g \times (y_A – y_B)}\]
En considérant que la vitesse initiale du sauteur au point A est nulle : \( v_A = 0 \, \text{m.s}^{-1} \)
\[ \mathrm{ \frac{1}{2} \times m \times v_B^2 – \frac{1}{2} \times m \times 0^2 = m \times g \times (y_A – y_B)}\]
\[ \mathrm{ \frac{1}{2} \times m \times v_B^2 = m \times g \times (y_A – y_B)}\]
\[ \mathrm{ v_B^2 = \frac{2 \times m \times g \times (y_A – y_B)}{m}}\]
\[ \mathrm{ v_B^2 = 2 \times g \times (y_A – y_B)}\]
On pose \( h = y_A – y_B \)
\[ \mathrm{ v_B = \sqrt{2 \times g \times h}}\]
1.1.4. Sur l’enregistrement réalisé, le sauteur commence à s’écarter de sa trajectoire verticale pour une hauteur h = 16 m (fin de la chute libre). Calculer la valeur de la vitesse au point B en utilisant l’expression établie à la question précédente.
\[ \mathrm{ v_B = \sqrt{2 \times g \times h}}\]
\[ \mathrm{ v_B = \sqrt{2 \times 9{,}81 \times 16}}\]
\[ \mathrm{ v_B = 18 \, \text{m.s}^{-1}}\]
1.2. Confrontation avec le saut réalisé
Voici une partie du code Python permettant de calculer la vitesse à partir des listes x et y, respectivement la liste des abscisses des points repérant le sauteur sur la vidéo et la liste des ordonnées de ces mêmes points. Les vitesses sont calculées avec la convention suivante :
- la vitesse en abscisses vx est définie comme l’abscisse du point suivant moins celle du point actuel, le tout divisé par la durée entre ces deux points notée dt. ;
- même convention pour l’axe des ordonnées.

1.2.1. Compléter les morceaux du code manquants entre les crochets lignes 56 et 57.
Ligne 56 vx = (x[k+1]-x[k])/dt
Ligne 57 vy = (y[k+1]-y[k])/dt
1.2.2. Expliquer ce que calcule la partie soulignée de la ligne 58, sachant que math.sqrt permet de calculer une racine carrée.
math.sqrt(vx*vx+ vy*vy)
sqrt : racine carrée
vx*vx : vx2
vy*vy : vy2 math.sqrt(vx*vx+vy*vy) calcule la valeur de la vitesse à l’aide des valeurs des vitesses sur l’axe x et valeurs des vitesses sur l’axe y :
\[ \mathrm{ v = \sqrt{v_x^2 + v_y^2}}\]
1.2.3. L’exploitation des résultats conduit à une vitesse au point B de 58 km.h–1 au cours du saut réalisé. Comparer cette valeur à celle déterminée à la question 1.1.4, proposer une explication à cet écart.
\[ \mathrm{ 58 \, \text{km.h}^{-1} = \frac{58}{3{,}6} \,=16 \text{m.s}^{-1}}\]
La valeur expérimentale de la vitesse est inférieure à la valeur théorique de la vitesse calculée à la question 1.1.4.
Cet écart s’explique par le fait que nous n’avons pas pris en compte, dans notre modèle théorique, les forces de frottements de l’air.
2. Étude de la phase du saut entre C et D
2.1. Donner l’expression de l’énergie cinétique du sauteur Ec en fonction de sa masse m et de sa vitesse v.
Ec =1/2×m×v2
2.2. Donner l’expression de l’énergie potentielle de pesanteur du sauteur Epp en fonction de sa masse m, de g et de son altitude y par rapport au sol.
Epp = m × g × y
2.3. Donner l’expression de son énergie mécanique Em.
Em =Ec +Epp
Em =1/2×m×v2+ m × g × y
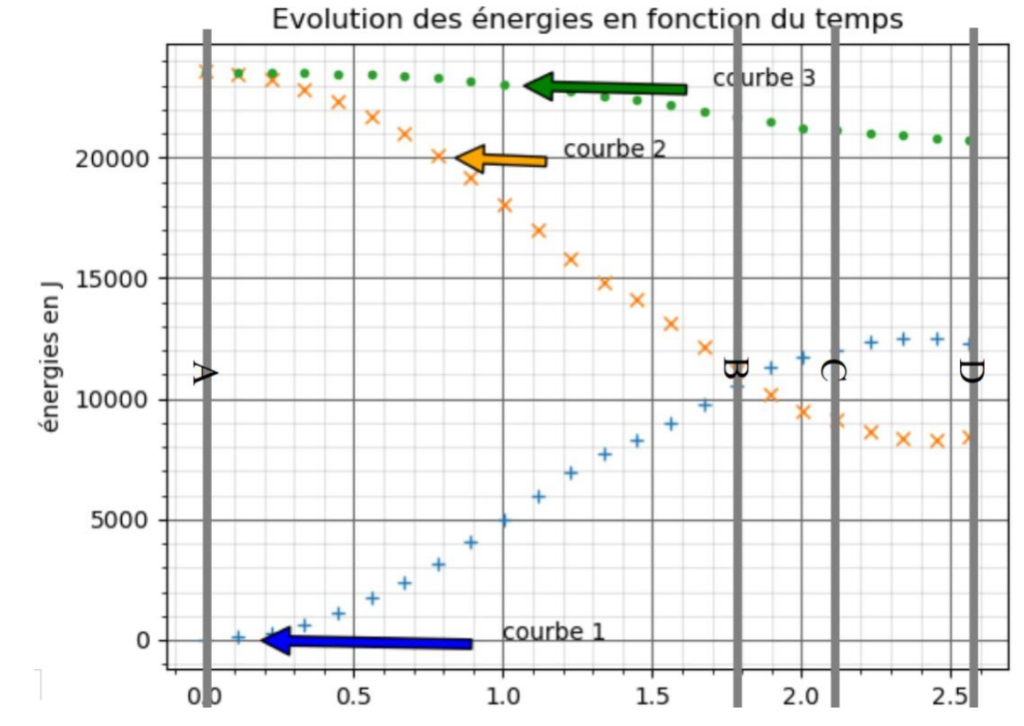
2.4. Identifier les courbes Ec, Epp et Em données dans le document 3. Justifier.
Epp = m × g × y : l’énergie potentielle de pesanteur est proportionnelle à l’altitude. Entre les points A et B, l’altitude y diminue donc Epp diminue : Courbe 2
Ec =1/2×m×v2 : la vitesse initiale du sauteur au point A est nulle. Ainsi, à l’instant initiale, la vitesse étant nulle, l’énergie cinétique est nulle. Lors de la décente, la vitesse augmente donc l’énergie cinétique augmente : courbe 1
Em =Ec +Epp : l’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur. La courbe la représentant est la somme des deux autres : courbe 3

2.5. L’hypothèse d’une chute libre sans frottements est-elle ici justifiée ? Pourquoi ?
Nous étudions de la phase du saut entre C et D.
L’énergie mécanique (courbe 3) est quasiment constante entre les points C et D. Les forces de frottements sont donc négligeables entre C et D. Dans notre cas, une chute libre sans frottements est justifiée.
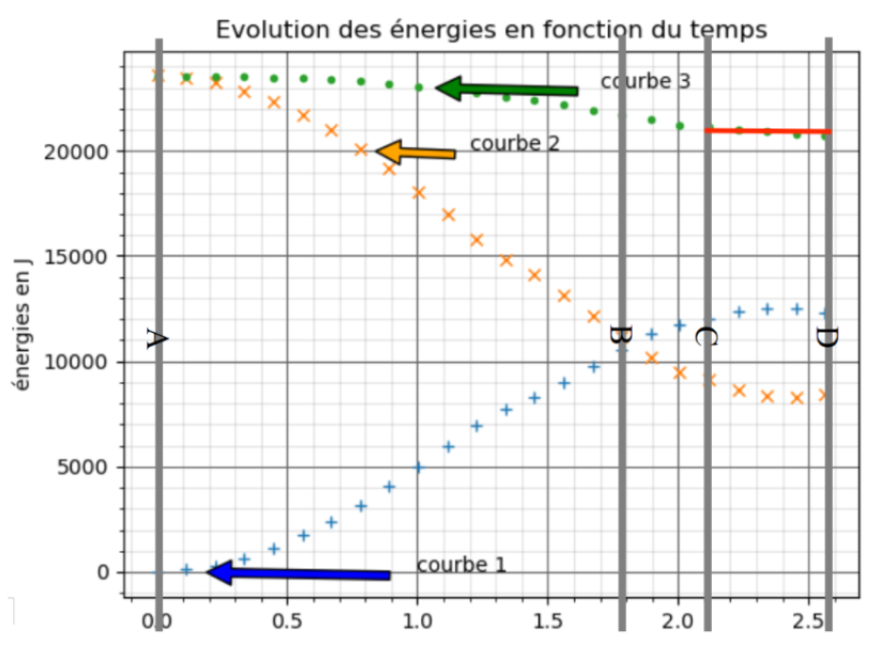
Remarque pour le saut entre la partie A et B (non demandée) : L’énergie mécanique (courbe 3) diminue entre les points A et B. Les forces de frottements ne sont donc pas négligeables. Dans notre cas, une chute libre sans frottements n’est pas justifiée.
2.6. D’après la courbe du document 3, pour quelle date t, le sauteur passe par sa position d’équilibre : la verticale ?
Lorsque le sauteur passe par sa position d’équilibre : la verticale, son altitude est au plus bas.
A la verticale son énergie potentielle (Courbe 2) de pesanteur est minimale.
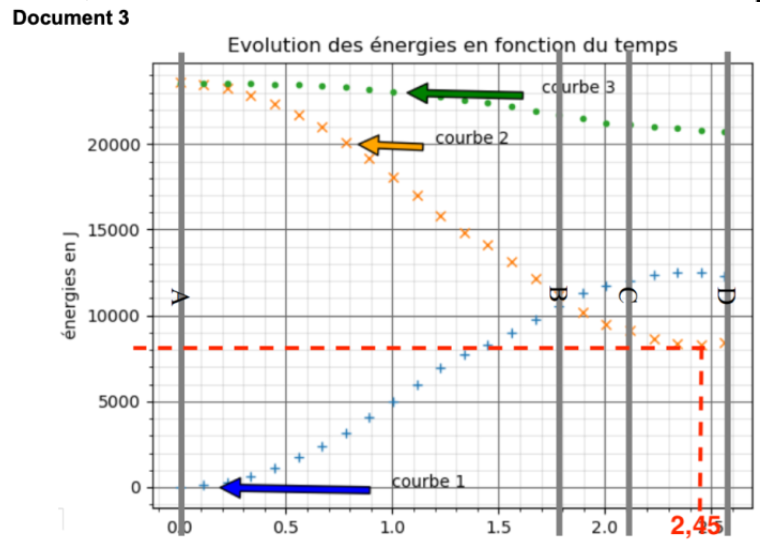
Le sauteur passe par sa position d’équilibre : la verticale, à la date t=2,45s.
2.7. En exploitant les courbes du document 3 et le passage par la position verticale, déterminer la longueur de la corde et vérifier l’affirmation du document 1 : pour un saut pendulaire, la longueur de chute libre atteint 80 % de sa hauteur, c’est à dire la longueur de la corde.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti.
Le sautoir se situe à une altitude yA = 30 m par rapport au sol. Pour un saut pendulaire, la longueur de chute libre atteint 80 % de sa hauteur. Calculons l’altitude qu’il doit atteindre pour être à 80 % de sa hauteur :
\[ \mathrm{ \text{80\%} \, y_A = \frac{80}{100} \times 30 = 24 \, \text{m}}\]
Il doit descendre de 24 m et donc atteindre une altitude de 30 – 24 = 6 m
A l’aide du document 3, calculons l’altitude atteinte à son point le plus bas (position d’équilibre : la verticale)
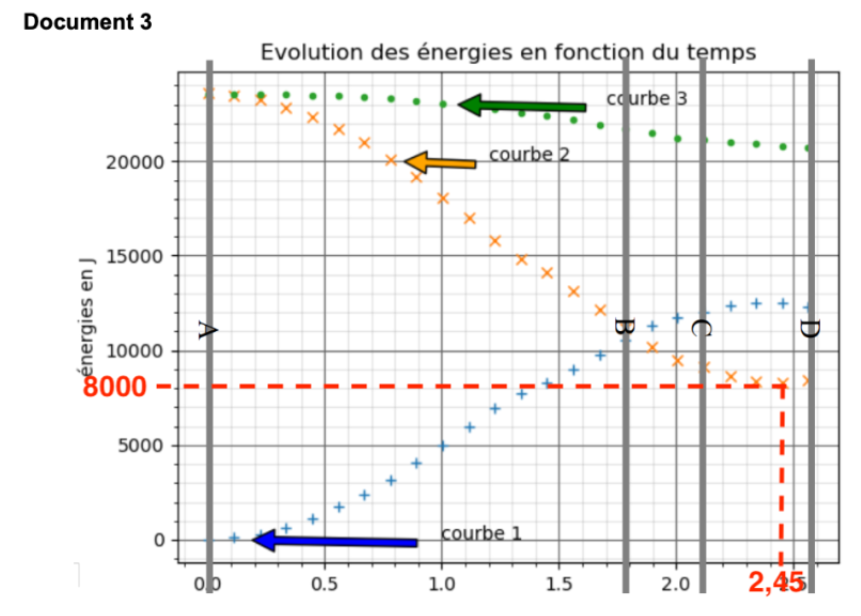
\[ \mathrm{ E_{pp} = m \times g \times y}\]
\[ \mathrm{ m \times g \times y = E_{pp}}\]
\[ \mathrm{ y = \frac{E_{pp}}{m \times g}}\]
\[ \mathrm{ y = \frac{8000}{80{,}0 \times 9{,}81}}\]
\[ \mathrm{ y = 10{,}2 \, \text{m}}\]
L’altitude minimale n’atteint pas les 6 m correspondant au 80 % de sa hauteur.
Ainsi, la longueur de chute libre n’atteint 80 % de sa hauteur.
