Le trombone de Koenig

Centres étrangers 2025 Sujet 2

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°25-PYCJ2G11

Le trombone de Koenig est un dispositif permettant de déterminer la célérité des ondes acoustiques. Il est composé de deux tubes en U emboîtés l’un dans l’autre. Le premier est fixe, le second est mobile. Un haut-parleur, alimenté par un générateur de basse fréquence, émet un son de fréquence fixe. Un microphone branché sur un oscilloscope mesure le signal à la sortie du dispositif. On suppose que les ondes ont la même amplitude dans les deux tubes et que leur propagation a lieu sans amortissement.

Lorsque le tube mobile est enfoncé au maximum (décalage nul), le dispositif est symétrique et les deux chemins suivis par les ondes ont la même longueur.

Lorsque le tube mobile est tiré, les deux chemins suivis sont différents : les ondes interfèrent.

D’après la Mission de Sauvegarde du Patrimoine Scientifique Technique Contemporain (patstec.fr)

Figure 1. Trombone de Koenig

L’objectif de cet exercice est de déterminer la célérité des ondes acoustiques dans l’air à 20 °C.

Figure 2. Le tube mobile est décalé vers la droite d’une distance d (le sens de propagation des signaux est représenté par une flèche) – Expérience 1

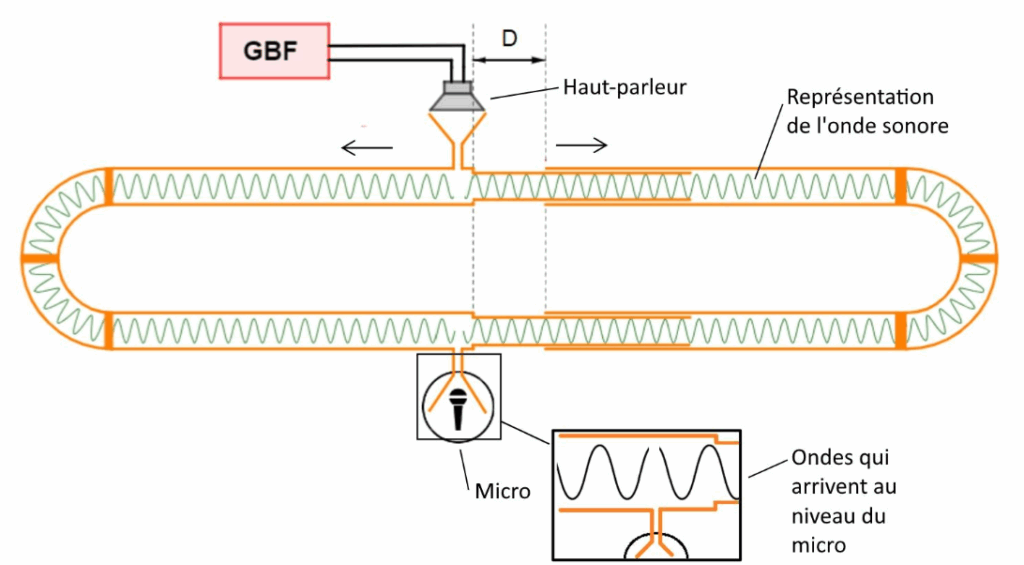
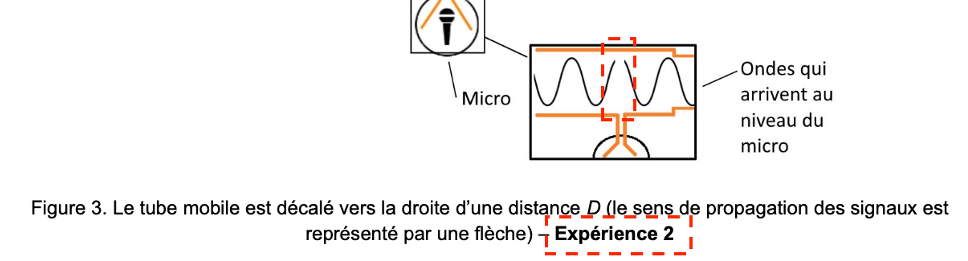
Figure 3. Le tube mobile est décalé vers la droite d’une distance D (le sens de propagation des signaux est représenté par une flèche) – Expérience 2

Q.1. Justifier en quoi le trombone de Koenig est un dispositif qui vérifie les conditions nécessaires à l’observation d’interférences au niveau du microphone.

Les ondes qui arrivent au niveau du micro proviennent d’une même source, elles sont cohérentes : elles ont la même fréquence et un déphase constant.

Sur l’écran de l’oscilloscope, on observe la figure suivante :

• la voie CH1 est reliée au GBF ;
• la voie CH2 est reliée au microphone.

Figure 4. Écran d’oscilloscope

Q.2. Préciser le type d’interférences observé sur la figure 4 et justifier si celle-ci est associée à l’expérience 1 ou à l’expérience 2.

Dans l’expérience 1 les ondes arrivent en opposition de phase : les interférences sont destructives.

Dans l’expérience 2 les ondes arrivent en phase : les interférences sont constructives.

Pour l’expérience 2, on définit δ, la différence de marche à l’instant t entre l’onde circulant dans le tube en U fixe et l’onde circulant dans le tube en U mobile.

Q.3. Exprimer $\delta$ en fonction de $D$.

D’après le sujet : « Pour l’expérience 2, on définit δ, la différence de marche à l’instant t entre l’onde circulant dans le tube en U fixe et l’onde circulant dans le tube en U mobile. »
$$\delta = d_{fixe} – d_{mobile}$$
Or on remarque que lorsque le tube est tiré, il y a une augmentation d’une distance D en haut et D en bas.
Ainsi :
$$\delta = 2D$$

Q.4. Rappeler la relation entre $\delta$ et $\lambda$, la longueur d’onde du signal sonore, dans le cas d’interférences constructives. On introduira dans cette relation un nombre entier positif $k$.

Dans le cas d’interférences constructives $$\delta = k \times \lambda$$ avec k un nombre entier positif.

Q.5. Montrer, à l’aide des questions 3 et 4, que pour tout $k$ entier positif, la distance de décalage correspondante $D\_k$, conduisant à des interférences constructives, peut se mettre sous la forme :

$$D_k = \dfrac{k}{2} \times \dfrac{v}{ f}$$

avec $v$ : célérité de l’onde sonore dans le trombone en $\mathrm{m\cdot s^{-1}}$ ; 
$f$ : fréquence de l’onde sonore dans le trombone en Hz.

$$\delta = 2D$$
$$2D = \delta$$
$$D = \frac{\delta}{2}$$

Or dans le cas d’interférences constructives $$\delta = k \times \lambda$$
$$D = \frac{k \times \lambda}{2}$$
$$D = \frac{k}{2} \times \lambda$$

Or
$$v = \lambda \times f$$
$$\lambda \times f = v$$
$$\lambda = \frac{v}{f}$$

D’où
$$D = \frac{k}{2} \times \frac{v}{f}$$
Ainsi
$$D_k = \frac{k}{2} \times \frac{v}{f}$$

La plus petite distance de décalage $D\_1$ permettant d’observer à l’écran des interférences constructives est $D\_1 = 4{,}35\ \mathrm{cm}$ pour une fréquence de l’onde sonore $f = 4\,032\ \mathrm{Hz}$.

Q.6. En déduire la valeur de la célérité de l’onde sonore se propageant dans le trombone de Koenig.

$$\frac{k}{2} \times \frac{v}{f} = D_k$$
$$v = \frac{2 \times D_k \times f}{k}$$

Pour $D_1$, $k = 1$ :
$$v = \frac{2 \times 4{,}35 \times 10^{-2} \times 4032}{1}$$
$$v = 351\ \text{m·s}^{-1}$$

On souhaite automatiser la détermination de la célérité v des ondes acoustiques, en exploitant toutes les valeurs D_k mesurées, à l’aide du programme écrit en langage python ci-dessous.

Figure 5. Programme permettant de déterminer la célérité et la longueur d’onde des ondes acoustiques

Q.7. Expliquer l’intérêt des lignes 8, 9 dans le programme.

Les lignes 8, 9 dans le programme permettent de calculer v pour différentes valeurs de k.

Q.8. Proposer à la ligne 16, à l’aide des grandeurs définies dans le programme, une formule permettant de calculer la longueur d’onde $\lambda$ (Lambda) des ondes acoustiques.

$$v = \lambda \times f$$
$$\lambda \times f = v$$
$$\lambda = \frac{v}{f}$$

Ligne 16 : Lambda = v_son/f