Le « tweener-lob » ou le coup entre les jambes

Bac La Réunion 2023 Sujet 1

Exercice 2 – (5 points) –  Durée 0h53 – Calculatrice autorisée

Sujet n°23-PYCJ1LR1

Sujet et corrigé

EXERCICE II – LE « TWEENER-LOB » OU LE COUP ENTRE LES JAMBES (5 points)

Lors des huitièmes de finale de Roland Garros en 2022, Carlos Alcaraz a réalisé un « tweener-lob » contre Karen Khachanov. Pour que le « tweener-lob » soit réussi, la balle doit passer au-dessus de l’adversaire et retomber avant la ligne de fond de court.

On s’intéresse dans cet exercice à ce geste tennistique. L’étude sera menée dans le référentiel terrestre supposé galiléen et le système {balle} sera considéré comme un point matériel noté 𝐺. On négligera tout type de frottement.

Source : www.tennislegend.fr

Carlos Alcaraz est situé sur la ligne de fond de court lorsqu’il joue son « tweener-lob ». Il frappe la balle à une hauteur 𝑦₀ = 30,0 cm et lui communique une vitesse $\overrightarrow{v_0}$ contenue dans un plan vertical, de valeur 𝑣₀ = 55,1 km⋅h⁻¹, et formant un angle 𝛼 = 48,0° avec l’horizontale.

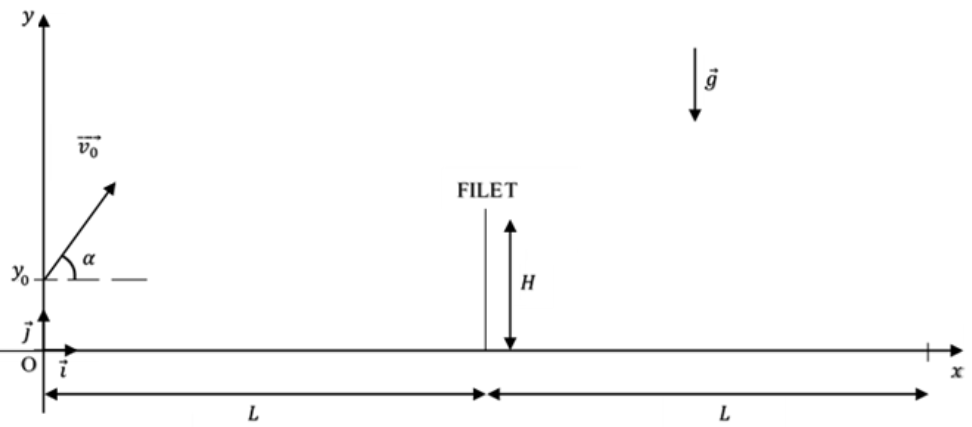
Figure 1 : Représentation schématique de la situation

Données :

• accélération de pesanteur : 𝑔 = 9,81 m. s⁻² ;
• masse de la balle : 𝑚 = 58,5 g ;
• longueur entre la ligne de fond de court et le filet : 𝐿 = 12,0 m ;
• hauteur du filet : 𝐻 = 0,914 m.

PARTIE A : Étude du mouvement de la balle lors du « tweener-lob »

A.1 En appliquant la deuxième loi de Newton, déterminer les coordonnées du vecteur accélération lors du mouvement de la balle dans le repère $(O;\vec{i};\vec{j})$.

Système {Balle}
Référentiel terrestre supposé galiléen
D’après la deuxième loi de newton :
$$\Sigma\overrightarrow{F_{ext}}=m\overrightarrow{a}$$
$$\overrightarrow{P}=m\overrightarrow{a}$$
$$m\overrightarrow{g}=m\overrightarrow{a}$$
$$\overrightarrow{g}=\overrightarrow{a}$$

Le vecteur accélération du centre d’inertie du solide est égal au vecteur champ de pesanteur.
$$\overrightarrow{a}\ \begin{pmatrix}a_{x(t)}=0 \\ {\ a}_{y\left(t\right)}=-g \end{pmatrix}$$

La balle est frappée à la date 𝑡 = 0 s.

A.2 Déterminer, en détaillant chaque étape de votre raisonnement, les équations horaires 𝑥(𝑡) et 𝑦(𝑡) du point 𝐺 dans le repère $(O;\vec{i};\vec{j})$.

$$\overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{v}\ \begin{pmatrix}v_{x(t)}=C_1 \\ {\ v}_{y\left(t\right)}=-gt+C_2 \end{pmatrix}$$
Pour trouver les constantes, on utilise ${\overrightarrow{v}}_0$
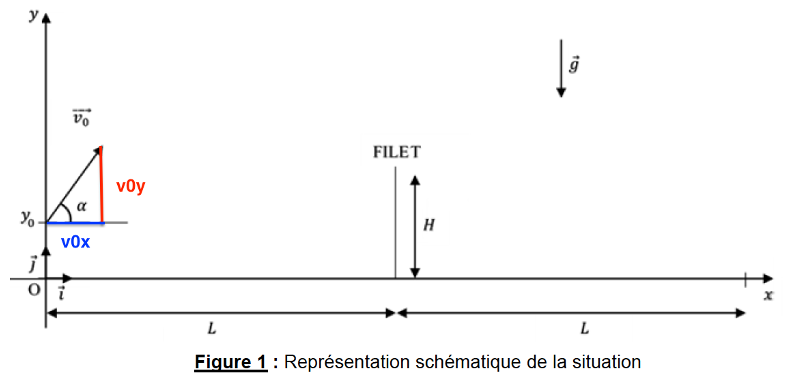
$${\overrightarrow{v}}_0\ \begin{pmatrix}v_{0x}=v_0\ cos\alpha \\ v_{0y}=v_0\ sin\ \alpha \end{pmatrix}$$

$$\overrightarrow{v}=\frac{d\overrightarrow{OG}}{dt}$$
On intègre le système d’équation précédent :
$$\overrightarrow{OG}\begin{pmatrix}x\left(t\right)=\ \ v_0\cos{\left(\alpha\right)}\times t\ +C_3 \\ y\left(t\right)=-\frac{1}{2}gt^2+v_0\sin{\left(\alpha\right)}\times t\ +C_4 \end{pmatrix}$$
Pour trouver les constantes, on utilise ${\overrightarrow{OG}}_0$
$${\overrightarrow{OG}}_0\ \begin{pmatrix}x_0=0 \\ y_0 \end{pmatrix}$$
d’ou
$$\overrightarrow{OG}\begin{pmatrix}x\left(t\right)=\ \ v_0\cos{\left(\alpha\right)}\times t \\ y\left(t\right)=-\frac{1}{2}gt^2+v_0\sin{\left(\alpha\right)}\times t+y_0 \end{pmatrix}$$

A.3 En déduire que l’équation de la trajectoire de la balle est, dans les unités du système international :

𝑦 = −0,047 𝑥² + 1,1 𝑥 + 0,30

On isole t :
$$x=v_0\cos{\left(\alpha\right)}\times t$$
$$v_0\cos{\left(\alpha\right)}\times t=x$$
$$t=\frac{x}{v_0\cos{\left(\alpha\right)}}$$

On remplace t dans y :
$$y\left(t\right)=-\frac{1}{2}gt^2+v_0\sin{\left(\alpha\right)}\times t+y_0$$
$$y\left(x\right)=-\frac{1}{2}g\left(\frac{x}{v_0\cos{\left(\alpha\right)}}\right)^2+v_0\sin{\left(\alpha\right)}\times \frac{x}{v_0\cos{\left(\alpha\right)}}+y_0$$
$$y\left(x\right)=-\frac{1}{2}g\frac{x^2}{v_0^2\cos^2{\left(\alpha\right)}}+x.\tan{\left(\alpha\right)}+y_0$$
$$y\left(x\right)=-\frac{1}{2}\times 9,8\times \frac{x^2}{\left(\frac{55,1}{3,6}\right)^2\cos^2{\left(48,0\right)}}+x.\tan{\left(48\right)}+30,0{\times 10}^{-2}$$
$$y\left(x\right)=-0,047x^2+1,1\ x+0,30$$

A.4 L’adversaire Karen Khachanov se situe à 3,0 m du filet et le tamis de sa raquette est alors à une hauteur de 4,0 m lorsque Carlos Alcaraz tente de le lober. Déterminer si la balle jouée par C. Alcaraz passe au-dessus de la raquette de son adversaire.

Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’est pas aboutie. La démarche est évaluée et nécessite d’être correctement présentée.

L’adversaire Karen Khachanov se situe à 3,0 m du filet :
$$x=L+3$$
$$x=12+3$$
$$x=15\ m$$

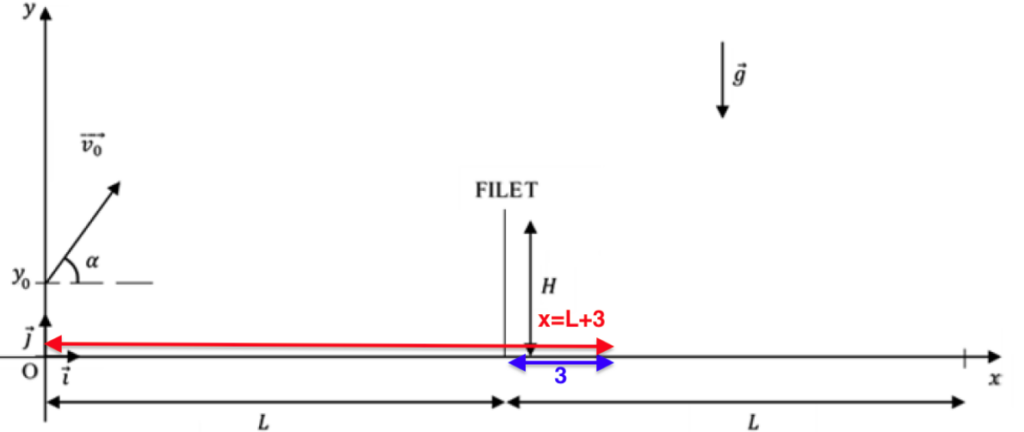
Calculons l’altitude de la balle pour x = 15 m :
$$y\left(x\right)=-0,047x^2+1,1\ x+0,30$$
$$y\left(x=15\right)=-0,047\times {15}^2+1,1\times 15+0,30$$
$$y\left(x=15\right)=6,2\ m$$
L’adversaire Karen Khachanov se situe à 3,0 m du filet et le tamis de sa raquette est alors à une hauteur de 4,0 m.
L’altitude de la balle pour x = 15 m est y = 6,2 m est supérieure à 4,0 m : La balle passe au-dessus de la raquette de son adversaire.

PARTIE B : Étude énergétique du mouvement de la balle

On choisira un axe vertical ascendant et une énergie potentielle de pesanteur nulle à l’origine du repère $(O;\vec{i};\vec{j})$.

À 𝑡 = 0 s, la balle est située au point (𝑥₀ = 0 ; 𝑦₀ = 0,30 m) avec une vitesse 𝑣₀ = 55,1 km⋅h⁻¹.

B.1 Rappeler la définition de l’énergie mécanique 𝐸_m de la balle.

L’énergie mécanique est la somme de l’énergie cinétique et l’énergie potentielle de pesanteur :
$$E_M=E_c+E_{pp}$$

B.2 Exprimer l’énergie mécanique 𝐸_m(0) de la balle à 𝑡 = 0 s, en fonction de 𝑚, 𝑔, 𝑣₀ et 𝑦₀. Calculer sa valeur.

$$E_M=E_c+E_{pp}$$
Avec :
$$E_c=\frac{1}{2}m.v^2$$
$$E_{pp}=mgy$$

$$E_M=\frac{1}{2}m.v^2+mgy$$

$$E_M\left(0\right)=\frac{1}{2}m.v_0^2+mgy_0$$
$$E_M\left(0\right)=\frac{1}{2}\times 58,5\times {10}^{-3}\times \left(\frac{55,1}{3,6}\right)^2+58,5\times {10}^{-3}\times 9,81\times 0,30$$
$$E_M\left(0\right)=7,0\ J$$

B.3 Indiquer sous quelle condition s’applique la conservation de l’énergie mécanique.

Lorsqu’il n’y a pas de frottements, la conservation de l’énergie mécanique s’applique.

B.4 Calculer la valeur de la vitesse de la balle 𝑣_𝑓 quand elle retombe au sol. Indiquer si la valeur réellement mesurée par le radar du terrain sera supérieure ou inférieure à celle calculée. Justifier.

D’après le sujet : « On négligera tout type de frottement ». On peut appliquer la conservation de l’énergie mécanique :
$$E_M\left(sol\right)=E_M\left(0\right)$$
$$E_c\left(sol\right)+E_{pp}\left(sol\right)=E_M\left(0\right)$$
$$\frac{1}{2}m.v_{sol}^2+mgy_{sol}=E_M\left(0\right)$$
Or $y_{sol}=0\ m$
$$\frac{1}{2}m.v_{sol}^2+mg\times 0=E_M\left(0\right)$$
$$\frac{1}{2}m.v_{sol}^2=E_M\left(0\right)$$
$$v_{sol}^2=\frac{2\times E_M\left(0\right)}{m}$$
$$v_{sol}=\sqrt{\frac{2\times E_M\left(0\right)}{m}}$$
$$v_{sol}=\sqrt{\frac{2\times 7,0}{58,5\times {10}^{-3}}}$$
$$v_{sol}=15,5\ m{.s}^{-1}$$
$$v_{sol}=15,5\times 3,6=55,8\ km{.h}^{-1}$$

La valeur réelle de la vitesse sera inférieure à celle trouvée à cause des forces de frottements.