Les comprimés de permanganate de potassium sont ils périmés ?

ÉVALUATION – 10 points – Durée 1h – calculatrice autorisée

Sujet 2024 n°SPEPHCH116 et n°SPEPHCH119

Un technicien trouve dans les réserves du laboratoire de chimie de son lycée des tubes de comprimés dont l’étiquette est reproduite ci-dessous

https://www.doctissimo.fr/ , guide des médicaments, permanganate potassium Lafran

Le technicien veut s’assurer qu’ils sont toujours conformes à la formulation donnée sur l’étiquette. Il réalise alors le titrage d’une solution obtenue en dissolvant un comprimé de permanganate dans de l’eau et en utilisant, comme solution titrante une solution de chlorure de fer II.

Données utiles pour tout l’exercice :

Masses molaires atomiques

potassium K : 39,1 g·mol⁻¹ ; manganèse Mn : 54,9 g·mol⁻¹; oxygène O : 16,0 g·mol⁻¹

Masses molaires moléculaires

chlorure de fer FeCl₂ : 127g·mol⁻¹;

permanganate de potassium KMnO₄ : 158 g·mol⁻¹.

Couples oxydant-réducteur : MnO₄^–(aq)/Mn²⁺(aq) ; MnO₂(s)/Mn²⁺(aq)
Couleurs de certaines espèces chimiques :

L’ion permanganate MnO₄^– (aq) est violet, le dioxyde de manganèse MnO₂(s) est marron, l’ion Fe²⁺(aq) est vert pâle, pratiquement incolore. Les ions potassium K⁺(aq) et chlorure Cl^–(aq) sont incolores.

Questions préalables

Sous forme de cristaux de couleur violette, soluble dans l’eau, le permanganate de potassium est un solide de formule KMnO₄ composé de cations K⁺(aq) et d’anions MnO₄^–(aq). […] En solution diluée le permanganate de potassium est utilisé pour le traitement de l’eau, notamment pour oxyder le fer et le manganèse dans les eaux souterraines.

D’après : http://www.societechimiquedefrance.fr/permanganate-de-potassium

1. Vérifier par un calcul la valeur de la masse molaire moléculaire du permanganate de potassium de 158 g·mol⁻¹.

Le permanganate de potassium a pour formule KMnO₄. Calculons la masse molaire moléculaire du permanganate de potassium :

$\mathrm{ M_{\text{KMnO}_4} = M_K + M_{\text{Mn}} + 4 \times M_O}$

$\mathrm{ M_{\text{KMnO}_4} = 39{,}1 + 54{,}9 + 4 \times 16{,}0}$

$\mathrm{ M_{\text{KMnO}_4} = 158 \, \text{g.mol}^{-1}}$

2. Vérifier par un calcul qu’une masse m = 0,25 g de permanganate de potassium pur contient une quantité de matière n = 1,6 mmol de permanganate de potassium.

$\mathrm{ n_{\text{KMnO}_4} = \frac{m_{\text{KMnO}_4}}{M_{\text{KMnO}_4}} }$

$\mathrm{ n_{\text{KMnO}_4} = \frac{0{,}25}{158}}$

$\mathrm{ n_{\text{KMnO}_4} = 1{,}6 \times 10^{-3} \, \text{mol}}$

$\mathrm{ n_{\text{KMnO}_4} = 1{,}6 \, \text{mmol}}$

Ainsi, une masse m = 0,25 g de permanganate de potassium pur contient une quantité de matière n = 1,6 mmol de permanganate de potassium.

Réaction support du titrage

L’équation de la réaction support du titrage des ions permanganate par les ions ferreux Fe²⁺ s’écrit :

MnO₄^–(aq) + 5 Fe²⁺(aq) + 8 H⁺(aq) → Mn²⁺(aq) + 5 Fe³⁺(aq) + 4 H₂O(l)

3. Justifier que pour procéder au titrage, le milieu doit être acidifié.

MnO₄^–(aq) + 5 Fe²⁺(aq) + 8 H⁺(aq) → Mn²⁺(aq) + 5 Fe³⁺(aq) + 4 H₂O(l)

Pour que la réaction ait lieu, des ions H⁺ sont nécessaire dans le milieu réactionnel. Ces ions sont apportés par un acide. Ainsi, pour procéder au titrage, le milieu doit être acidifié.

4. Écrire les couples oxydant-réducteur mis en jeux dans la réaction support du titrage.

MnO₄^–(aq) + 5 Fe²⁺(aq) + 8 H⁺(aq) → Mn²⁺(aq) + 5 Fe³⁺(aq) + 4 H₂O(l)

Données : Couples oxydant-réducteur : MnO₄^–(aq)/Mn²⁺(aq) ; MnO₂(s)/ Mn²⁺(aq)

On choisit parmi ces couple le couple dans lequel MnO₄^–(aq) et Mn²⁺(aq) apparaissent.

1er couple : MnO₄^–(aq)/Mn²⁺(aq)
Pour le second on a Fe²⁺(aq) et Fe³⁺(aq). Sachant que MnO₄^–(aq) est l’oxydant de la réaction (il est a gauche du 1er couple), Fe²⁺(aq) qui réagit avec lui est le réducteur.
On obtient ainsi le 2nd couple: Fe³⁺(aq)/Fe²⁺(aq)

5. Écrire les demi-équations électroniques associées à chacun de ces couples.

$\mathrm{ \text{MnO}_4^- \, (\text{aq})/\text{Mn}^{2+} \, (\text{aq}) \quad \text{∶} \quad \text{MnO}_4^- \, (\text{aq}) + 8\text{H}^+ \, (\text{aq}) + 5\text{e}^- = \text{Mn}^{2+} \, (\text{aq}) + 4\text{H}_2 \text{O} \, (\text{l})}$

$\mathrm{ \text{Fe}^{3+} \, (\text{aq})/\text{Fe}^{2+} \, (\text{aq}) \quad \text{∶} \quad \text{Fe}^{3+} \, (\text{aq}) + \text{e}^- = \text{Fe}^{2+} \, (\text{aq})}$

Montage expérimental

Le technicien s’interroge sur la place des solutions dans le montage expérimental. Bien que la solution de permanganate de potassium soit l’espèce titrée, il décide, après documentation, de la placer dans la partie haute du montage (voir figure ci-dessous) et de placer la solution titrante d’ions ferreux S₁ dans la partie basse. Ce choix est fait, car cela permet d’éviter le contact prolongé entre les ions permanganate MnO₄^–(aq) et les ions manganèse Mn²⁺(aq) formés, qui engendrerait une réaction parasite et le « noircissement » du milieu réactionnel.

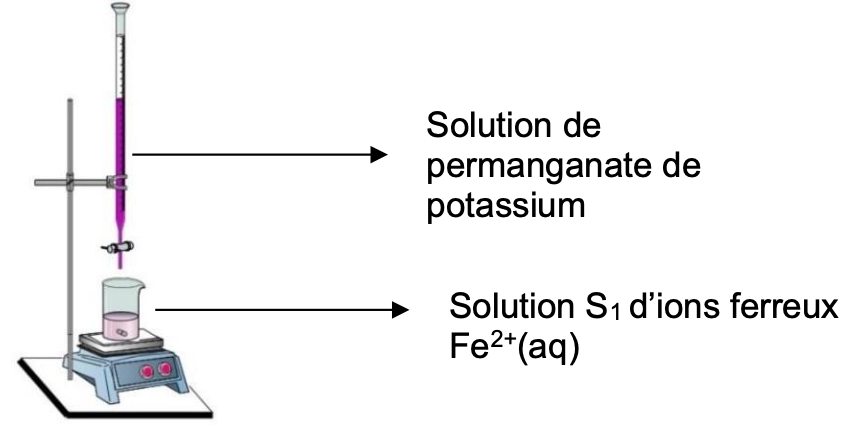
6. Nommer les éléments de verrerie contenant respectivement la solution de permanganate de potassium et la solution d’ions ferreux.

Verrerie contenant la solution de permanganate de potassium : burette graduée.

Verrerie la solution d’ions ferreux : bécher.

Choix de la concentration de la solution titrante d’ions ferreux

Le technicien s’interroge ensuite sur la concentration de la solution titrante S₁ d’ions ferreux placée dans le bécher. Il choisit de travailler avec un volume V₁ = 20,0 mL de cette solution S₁ d’ions ferreux.

Son objectif est que, dans le cas d’un comprimé de permanganate de potassium non périmé, cette concentration de la solution titrante S₁ d’ions ferreux soit telle que l’équivalence du titrage se produise pour un volume de permanganate versé situé approximativement au milieu de la burette soit 12,5 mL environ.

Il décide de rédiger un programme en langage Python lui permettant de déterminer la concentration de la solution titrante S₁ d’ions ferreux à utiliser, et de suivre l’évolution de la quantité de matière en ions Fe²⁺ dans le bécher en fonction du volume de solution de permanganate de potassium versé.

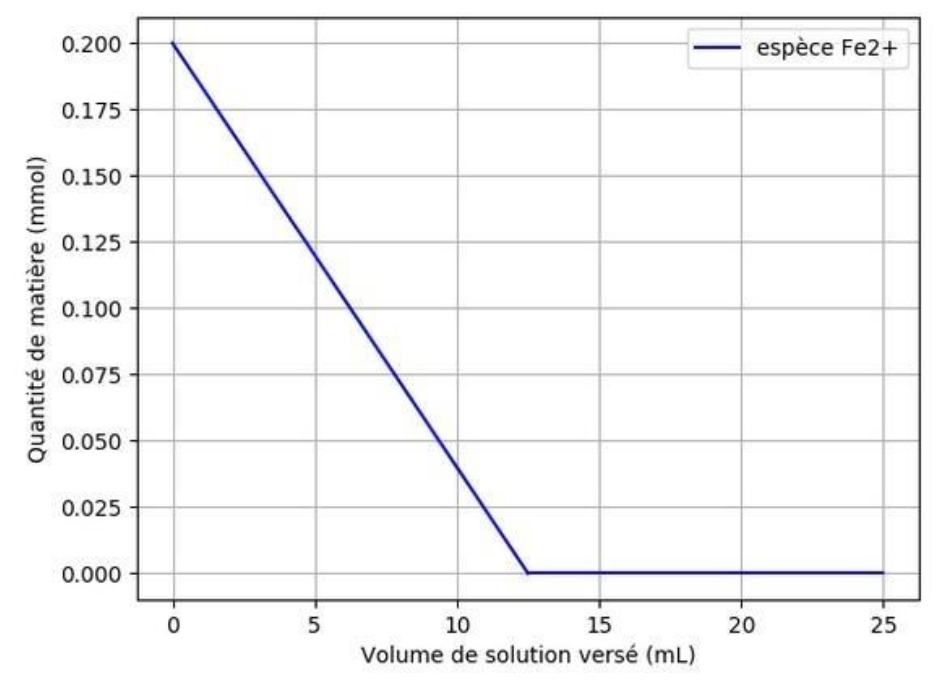
L’exécution du programme en langage Python permet d’obtenir la courbe suivante :

7. Définir l’équivalence d’un titrage.

L’équivalence est atteinte lorsque les réactifs ont été introduits dans les proportions stœchiométriques.

Le technicien prépare la solution S₀ de permanganate de potassium à titrer en dissolvant un comprimé de permanganate de potassium dans un volume V₀ = 0,50 L d’eau distillée.

8. Vérifier par un calcul que, dans le cas d’un comprimé non périmé, la concentration C₀ en ions MnO₄^– (aq) dans cette solution correspond à celle mentionnée en ligne 4 du programme.

$\mathrm{c_0 = \frac{n}{V_0}}$

$\mathrm{c_0 = \frac{1{,}6 \times 10^{-3}}{0{,}50}}$

$\mathrm{c_0 = 3{,}2 \times 10^{-3} \, \text{mol} \cdot \text{L}^{-1}}$

$\mathrm{c_0 = 3{,}2 \, \text{mmol} \cdot \text{L}^{-1}}$

Dans le cas d’un comprimé non périmé, la concentration C₀ en ions MnO₄^— (aq) dans cette solution correspond bien à celle mentionnée en ligne 4 du programme : 3,2 mmol.L^—1.

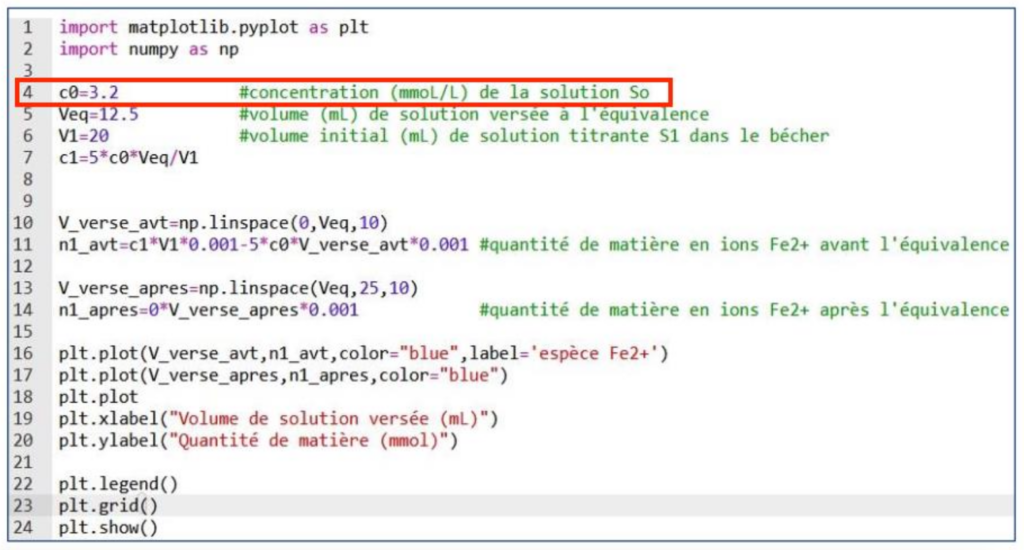
La ligne 7 du programme en langage Python code la formule littérale permettant le calcul de la concentration en ions ferreux de la solution S₁ à préparer.

9. Vérifier la formule littérale utilisée en s’aidant de l’équation de la réaction support du titrage.

$\mathrm{\text{MnO}_4^- \,(\text{aq}) + 8\text{H}^+ \,(\text{aq}) + 5\text{Fe}^{2+} \,(\text{aq}) \longrightarrow \text{Mn}^{2+} \,(\text{aq}) + 4\text{H}_2\text{O} \,(\text{l}) + 5\text{Fe}^{3+} \,(\text{aq})}$

À l’équivalence, les réactifs ont été introduits dans les proportions stœchiométriques :

$\mathrm{\frac{n(\text{Fe}^{2+})}{5} = \frac{n(\text{MnO}_4^-)_\text{vE}}{1}}$

$\mathrm{\frac{c_1 V_1}{5} = \frac{c_0 V_\text{eq}}{1}}$

$\mathrm{c_1 = \frac{5 \times c_0 V_\text{eq}}{V_1}}$

La formule littérale utilisée dans le programme en ligne 7 est conforme à celle trouvée.

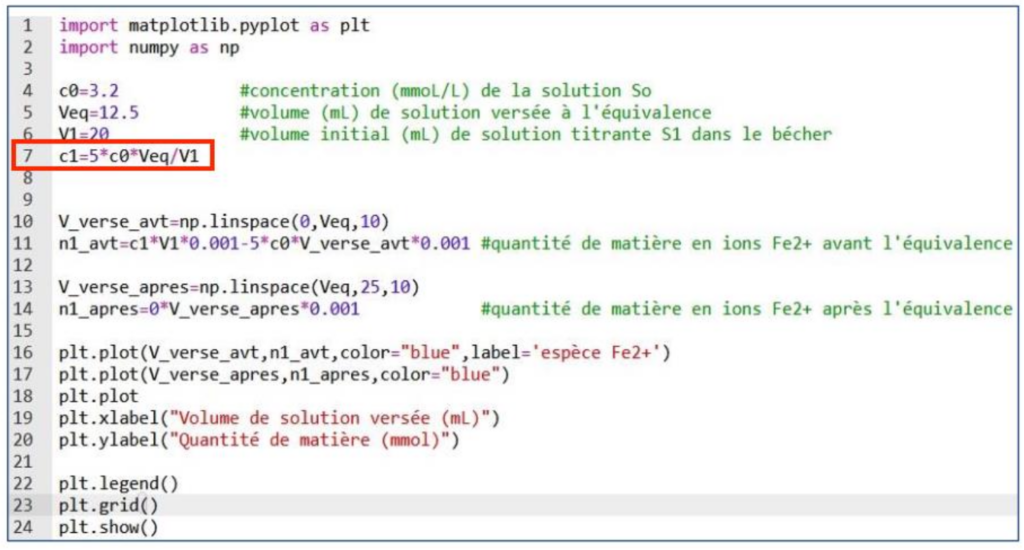
10. Vérifier que la valeur de la concentration en ions ferreux Fe²⁺ de la solution S₁ à préparer est C₁ = 1,0.10^-2 mol·L^-1.

$\mathrm{ c_1 = \frac{5 \times c_0 \times V_{\text{eq}}}{V_1}}$

$\mathrm{ c_1 = \frac{5 \times 3{,}2 \times 10^{-3} \, \text{mol} \cdot \text{L}^{-1} \times 12{,}5 \, \text{mL}}{20{,}0 \, \text{mL}}}$

$\mathrm{ c_1 = 1{,}0 \times 10^{-2} \, \text{mol} \cdot \text{L}^{-1}}$

La concentration en ions ferreux Fe²⁺ de la solution S₁ à préparer est C₁ = 1,0.10^-2 mol·L^-1.

11. Ecrire une ligne de code (en ligne 8 par exemple) pour que la valeur de la concentration de la solution S₁ à préparer apparaisse à l’écran lors de l’exécution de son programme.

Ligne 8 : print(c1) # La valeur de la concentration de la solution S₁ à préparer apparait à l’écran lors de l’exécution de son programme.

12. Commenter l’allure de la courbe obtenue à l’issue de l’exécution du programme.

Cette courbe décrit l’évolution de la quantité de matière des ions Fe²⁺.

Avant l’équivalence, les ions Fe²⁺ réagissent, leur quantité de matière diminue. Cela correspond à la première partie de la courbe.

Après l’équivalence, il n’y a plus d’ions Fe²⁺. La quantité de matière des ions Fe²⁺ est nulle. Cela correspond à la deuxième partie de la courbe.

Réalisation du titrage des ions permanganate par les ions ferreux

Le technicien réalise maintenant le titrage d’un comprimé de permanganate de potassium. Il prépare donc un volume V₀ = 0,50 L d’une solution aqueuse S₀ en dissolvant un comprimé de permanganate de potassium et il l’acidifie avec quelques gouttes d’acide sulfurique concentré. Il prépare son montage puis il verse progressivement cette solution dans un volume V₁ = 20,0 mL de solution S₁ d’ions ferreux de concentration en ions ferreux C₁ = 1,0.10^-2 mol·L^-1.

13. Expliquer comment le technicien saura qu’il a atteint l’équivalence.

L’ions Fe²⁺ est vert pâle, pratiquement incolore et le permanganate de potassium est violet.

Avant l’équivalence, le permanganate de potassium est le réactif limitant et l’ions Fe²⁺ le réactif en excès. Le mélange est de la couleur du réactif en excès : il est vert pâle, pratiquement incolore.

Après l’équivalence, le permanganate de potassium est le réactif en excès et l’ions Fe²⁺ le réactif limitant. Le mélange est de la couleur du réactif en excès : il est magenta.

Ainsi, à l’équivalence on observe un changement de couleur du vert pâle, pratiquement incolore au violet.

Le technicien saura qu’il a atteint l’équivalence avec le changement de couleur.

Il juge que l’équivalence est atteinte lorsqu’il a versé un volume V_eq = 12,8 mL de solution de permanganate de potassium.

14. Déterminer la masse de permanganate de potassium dans le comprimé utilisé et l’écrire avec le nombre adapté de chiffres significatifs sachant que l’incertitude-type de la mesure de la masse u(m) = 0,003 g. Comparer qualitativement ce résultat à la valeur de référence de l’étiquette.

$\mathrm{ \text{MnO}_4^- (\text{aq}) + 8\text{H}^+ (\text{aq}) + 5\text{Fe}^{2+} (\text{aq}) \rightarrow \text{Mn}^{2+} (\text{aq}) + 4\text{H}_2 \text{O} (\ell) + 5\text{Fe}^{3+} (\text{aq})}$

À l’équivalence, les réactifs ont été introduits dans les proportions stœchiométriques :

$\mathrm{ \frac{n(\text{MnO}_4^-)_\text{eq}}{1} = \frac{n(\text{Fe}^{2+})}{5}}$

$\mathrm{ n(\text{MnO}_4^-)_\text{eq} = \frac{n(\text{Fe}^{2+})}{5}}$

$\mathrm{ n(\text{MnO}_4^-)_\text{eq} = c_{\text{MnO}_4^-} \times V_\text{eq}}$

$\mathrm{ n(\text{Fe}^{2+}) = c_1 \times V_1}$

D’où

$\mathrm{ c_{\text{MnO}_4^-} \times V_\text{eq} = \frac{c_1 \times V_1}{5}}$

$\mathrm{ c_{\text{MnO}_4^-} = \frac{c_1 \times V_1}{5 \times V_\text{eq}}}$

$\mathrm{ c_{\text{MnO}_4^-} = \frac{1,0 \times 10^{-2} \times 20,0}{5 \times 12,8}}$

$\mathrm{ c_{\text{MnO}_4^-} = 3,1 \times 10^{-3} \, \text{mol} \cdot \text{L}^{-1}}$

Déterminons la masse de permanganate de potassium dans le comprimé utilisé :

$\mathrm{ c_{\text{MnO}_4^-} = \frac{n(\text{MnO}_4^-)}{V_0}}$

$\mathrm{ n(\text{MnO}_4^-) = c_{\text{MnO}_4^-} \times V_0}$

$\mathrm{ n(\text{MnO}_4^-) = \frac{m(\text{MnO}_4^-)}{M(\text{MnO}_4^-)}}$

d’où

$\mathrm{ \frac{m(\text{MnO}_4^-)}{M(\text{MnO}_4^-)} = c_{\text{MnO}_4^-} \times V_0}$

$\mathrm{ m(\text{MnO}_4^-) = c_{\text{MnO}_4^-} \times V_0 \times M(\text{MnO}_4^-)}$

$\mathrm{ m(\text{MnO}_4^-) = 3,1 \times 10^{-3} \times 0,50 \times 158,0}$

$\mathrm{ m(\text{MnO}_4^-} = 0,18 \, \text{g}}$

Sachant que l’incertitude-type de la mesure de la masse $u(m) = 0,003 \, \text{g}$ :

$\mathrm{ m(\text{MnO}_4^-) = 0,18 \pm 0,003 \, \text{g}}$

L’incertitude porte sur le 3e chiffre après la virgule, on ajoute un chiffre significatif au résultat trouvé pour qu’il ait 3 chiffres après la virgule :

$\mathrm{ m(\text{MnO}_4^-) = 0,184 \pm 0,003 \, \text{g}}$

La valeur de référence de l’étiquette est 0,25 g. La valeur trouvée est inférieure : Les comprimés de permanganate de potassium sont donc périmés.